MSE publications / references in 2014.
Bounty 100 raised for:
Create a number by multi by 2 and divide by 3 (integer part)
& BACKUP
Five attempts have been made:
Can any positive real be approximated as $2^m/3^n$ with $(m,n)$ large enough?
& BACKUP
Free accompanying (Delphi Pascal) source code available for this problem:
- Grafisch.pas : Helper routines
- Unit12.pas : Making of graph (1)
- Unit13.pas : Making of graph (2)
Double refinement of Nesbitt's inequality
& BACKUP
Free accompanying (Delphi Pascal) source code available for this problem:
- Contours.pas : the Art of Contouring
- Generaal.pas : General helper routines
- Grafisch.pas : Graphics helper routines
- Unit7.pas : Calculating the Isolines
- Unit8.pas : Graph of $\color{red}{f(x)}$ and $\color{blue}{g(x)}$
- Proef.dpr : Far away region calculations
Stern Brocot tree sequence
& BACKUP
Can the Stern-Brocot tree be employed for better convergence of $2^m/3^n$?
Free accompanying (Delphi Pascal essentials) source code available for this problem:
& BACKUP
Does there exist a real function with following properties?
& BACKUP (deleted)
Grid coordinates $\Longleftrightarrow$ Triangle numbering
Free accompanying (Delphi Pascal essentials) source code available for this question:
Free accompanying (Delphi Pascal) source code available with the answer:
& BACKUP
Length of a line inside a rectangle & BACKUP
Free accompanying (Delphi Pascal essentials) source code available with the answer:
It is noticed that this problem is very much related to the isolines refinement in:
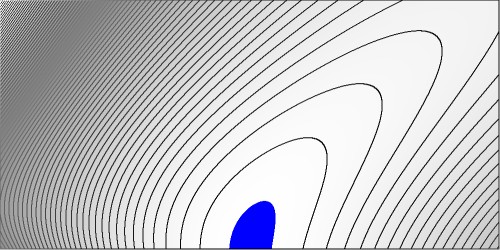
Find the area enclosed by $\sqrt{(x-2)^2+(y-3)^2} + 2\sqrt{(x-3)^2+(y-1)^2} = 4$
& BACKUP
Derivative and inverse
& BACKUP
Free accompanying (Delphi Pascal essentials) source code available with the answer:
The Method Of Frobenius & BACKUP
Free accompanying (Delphi Pascal essentials) source code available with the answer:
The numerical method in the software is based upon an old sci.math article,
where the constant frequency $\omega = \mbox{oo}$ has been replaced by $\omega = 1/x$.
How wide can a unit-length planar curve be? & BACKUP
Free accompanying (Delphi Pascal essentials) source code available with the answer:
Why does ${x}^{x^{x^{x^{\,.^{\,.^{\,.}}}}}}$ bifurcate below $\sim0.065$? & BACKUP
Free accompanying (Delphi Pascal essentials) source code available with the question:
How to find the slope of certain lines matching random points & BACKUP
Free accompanying (Delphi Pascal essentials) source code available with the answer:
How to approximate a sharply peaked function with deltas? & BACKUP
Is this Laplace BVP well posed? If not, why? & BACKUP
Free accompanying (Delphi Pascal essentials) source code available with the answer:
How about Cantor's Theory in a Finite context? & BACKUP
Free accompanying (Delphi Pascal essentials) source code available with the answer:
Simplify $N^{N(N-2)}$ with $N=(1\pm i\sqrt{3})/2$ & BACKUP
Is there a closed form for $\sum_{i=1}^n \left(\frac{i}{x + i}\right)^{i y}$? & BACKUP
Where are the Bessel functions in $\int_{0}^{2\pi}\int_{0}^{2\pi}e^{i\alpha[\sin(\theta)-\sin(\varphi)]}d\theta d\varphi$ ?
& BACKUP
Express $\mathrm{Tr}(X)$ in terms of $A$, given that $X=A^TX(I+X)^{-1}A$
& BACKUP
Explicit formula of the solution of $u_{tt}=au_{xx}$ and for which values of a is this a "wave equation"?
& BACKUP
What is a normal at the surface of a hypersphere?
& BACKUP
Problem with normal derivative
& BACKUP
When do equations represent the same curve?
& BACKUP
Subset as arithmetic mean of geometric means. Not really?
& BACKUP
Conjecture with the CGM of a Circle & BACKUP
Find the area of an isosceles trapezoid $ABCD$ $(AB\parallel CD)$
with height $m$ and perpendicular diagonals $(AC\perp BD)$
& BACKUP
Kernel of Integral Operator of the Newton Equation & BACKUP
Conservation laws in the finite element method for domains with curved boundaries
& BACKUP
Show that the tangent plane of the of the cone intersects the cone in a line
- help in communicating idea correctly
& BACKUP
How to rotate a rectangle inside a rectangle with different scales
& BACKUP
Derivation of bounds of convergence of infinite tower
& BACKUP
Can every continuous function be continuously "transformed" into a differentiable function?
& BACKUP (deleted)
Conjecture with a three-diagonal system of equations & BACKUP
which is the direct and inverse transformation matrix? & BACKUP
Prove or disprove that the function is convex & BACKUP
Prove or disprove that $f_n(x)\gt -1/2$ & BACKUP
Characteristics of equations of the form $u_{xy}=f(u_x,u_y,u)$ & BACKUP
How to represent a decimal number into a binary expression of a different radix/base
deleted & BACKUP
Expressing the 2D Laplacian using information given on a parametric curve
& BACKUP
What's going on with this infinite product? & BACKUP
Last attempt about the Cirtoaje's inequality $x^{\left(2\left(1-x\right)\right)^{k}}+(1-x)^{\left(2\left(x\right)\right)^{k}}\leq 1$
& BACKUP
Robust Least Squares for general 2D lines & BACKUP
Least square fit of ellipse worsens with increasing border thickness
& BACKUP (deleted)
Whenever we get undefined or indeterminate expressions in the real world, do we just take the limit, if it exists?
& BACKUP
The ellipse is known, but how to draw it? & BACKUP