MSE

Grid coordinates $\Longleftrightarrow$ Triangle numbering

Pictures say more than a thousand words.
Grid coordinates $\Longleftrightarrow$ Triangle numbering:

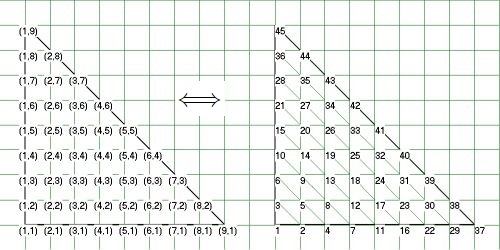
Poorman's option. I have tabulated, not "formulated" the values in the second picture. It has been done for a grid that is such that the horizontal / vertical legs of our isosceles right triangle contains $n=9$ gridpoints. Of course, we seek to generalize this for abitrary $n$.
What I need first is a formula or a short algorithm (preferrably a one-liner) that converts Grid coordinates into Triangle numbering. Call this function $\,\operatorname{nr}(i,j)\,$, giving as shown in the pictures:

  nr(1,1) = 1; nr(2,1) = 2; nr(1,2) = 3; nr(3,1) = 4; nr(2,2) = 5; nr(1,3) = 6; and so on

And also the other way around, formulas or short algorithms that converts Triangle numbering into Grid coordinates. Call them $\,\operatorname{nr2i}(n)\,$ and $\,\operatorname{nr2j}(n)\,$. Examples as in the pictures:

  nr2i(1) = 1; nr2j(1) = 1; nr2i(2) = 2; nr2j(2) = 1; nr2i(3) = 1; nr2j(3) = 2; and so on

A hint may be that arithmetic sequences are involved with $\,\operatorname{nr}(i,j)$: $1+2+3+\cdots +n=n(n+1)/2\,$. And the sum $\,(i+j)\,$ is a constant for one green $\color{green}{\bf \mbox{\\}}$ "level".

EDIT.

Implementation of the answer given by cr001 has been done as follows. My favorite programming language is Pascal.

function nr(i,j : integer) : integer;
begin
  nr := (((i+j-1)*(i+j)) div 2)-(i-1);
end;

function nr2i(n : integer) : integer;
var
  h : integer;
begin
  h := Trunc(1/2+sqrt(2*n))+1;
  nr2i := (((h-1)*h) div 2)-(n-1);
end;

function nr2j(n : integer) : integer;
var
  h : integer;
begin
  h := Trunc(1/2+sqrt(2*n))+1;
  nr2j := h - nr2i(n);
end;

Testing involves the fact that composing a function with its inverse reproduces identity:

n = nr(nr2i(n),nr2j(n));
i = nr2i(nr(i,j)); j = nr2j(nr(i,j));