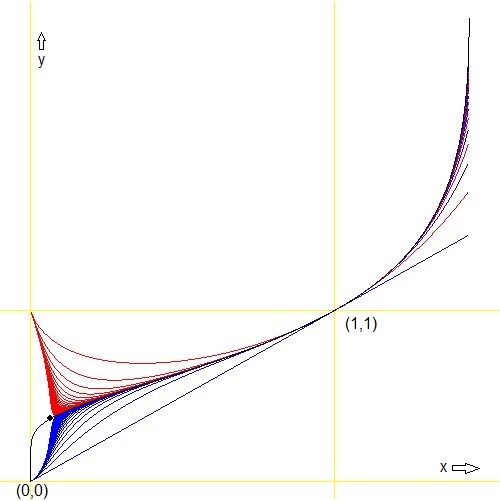

The $\color{blue}{blue\;lines}$ are the iterands for $n=$ odd; the $\color{red}{red\;lines}$ are the iterands for $n=$ even.
It is seen that splitting up odd and even starts at $x\lt 1$ and that there is a bifurcation point (black dot).
Going to infinity leads to the functional equation:
$$
y = x^y \quad \mbox{with} \quad y = h(x)
$$
The inverse function (where it exists) has an explicit analytical form, which is the black line in the above figure:
$$
x = y^{1/y}
$$
And can be used to establish the rightmost bound of the tower's domain:
$$
\frac{d}{dy}y^{1/y} = e^{\ln(y)/y}\left[-\frac{\ln(y)}{y^2}+\frac{1}{y^2}\right] = 0
\\ \Longrightarrow \quad \ln(y)=1 \quad \Longrightarrow \quad y=e \; ; \; x=e^{1/e}
$$
But in order to answer the question as stated, we have to consider another functional equation, namely:
$$
y = x^{x^y}
$$
Odd and even are separated now, as is required for observing the bifurcation.
There is no neat inverse function of the latter equation. Therefore we shall investigate the two-dimensional
funcion $\,f(x,y)=x^{x^y}-y\,$. An insightful way to do this is make an isoline chart / contour plot of the function.
Lines are darker where the contour levels are higher. The massive black line is the place where $f(x,y)=0$.
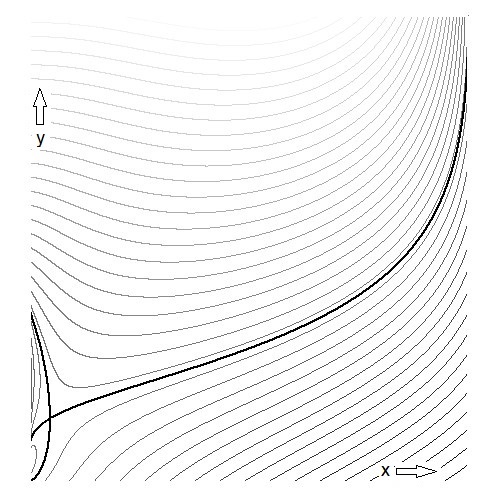
Implicit differentiation is employed for finding the derivatives: $$ df = \frac{\partial f}{\partial x} dx + \frac{\partial f}{\partial y} dy \\ df = x^{x^y}\left[\frac{x^y y \ln(x)}{x} + \frac{x^y}{x}\right] dx + \left[x^{x^y}x^y\ln^2(x)-1\right] dy $$ If the gradient is zero, then $f(x,y)$ has a critical point at that place: $$ \begin{cases} \partial f/\partial x = 0 & y \ln(x)+1 = 0 \\ \partial f/\partial y = 0 & x^{x^y}x^y\ln^2(x)-1=0 \end{cases} $$ Both equations are essentially the same, because $\,x^{x^y}=x^y=y\,$, giving with $\,x=y^{1/y}\,$: $$ y \ln(y^{1/y})+1 = \ln(y)+1 = 0 \quad \Longrightarrow \quad y = 1/e \quad ; \quad x = e^{-e} $$ If we look at the picture with the isolines, then it is evident that the bifurcation must be at this place, with coordinates $\,(x,y)=(e^{-e},1/e)\,$.
EDIT.
It is observed in the last picture that the isolines in the neighborhood of the critical point are like hyperbolas. To confirm this observation, the second order derivatives at the bifurcation point should be investigated as well. Let a computer algebra system (MAPLE) do the hard work.
> f(x,y) := x^(x^y)-y;
> A(x,y) := diff(diff(f(x,y),x),x);
> B(x,y) := diff(diff(f(x,y),x),y);
> C(x,y) := diff(diff(f(x,y),y),y);
> D(x,y) := diff(diff(f(x,y),y),x);
> a := simplify(subs({x=exp(1)^(-exp(1)),y=1/exp(1)},A(x,y)));
exp(-3 + 2 exp(1))
> b := simplify(subs({x=exp(1)^(-exp(1)),y=1/exp(1)},B(x,y)));
-exp(-1 + exp(1))
> c := simplify(subs({x=exp(1)^(-exp(1)),y=1/exp(1)},C(x,y)));
0
> d := simplify(subs({x=exp(1)^(-exp(1)),y=1/exp(1)},D(x,y)));
-exp(-1 + exp(1))
So the Hessian matrix at the critical point is:
$$
\begin{bmatrix}
a & b \\
b & c
\end{bmatrix} =
\begin{bmatrix}
e^{-3+2e} & -e^{-1+e} \\
-e^{-1+e} & 0 \end{bmatrix}
$$
And the two eigenvalues of the Hessian turn out to be
$$
\lambda_{1,2} = \frac{a+c}{2} \pm \sqrt{b^2 + \left(\frac{a-c}{2}\right)^2} \\ =
\frac{1}{2} e^{-3+2e} \left[1 \pm \sqrt{\left(2\frac{e^{-1+e}}{e^{-3+2e}}\right)^2+1}\right]
$$
Herewith it is clear that one eigenvalue is positive while the other is negative.
Therefore the critical point is a saddle point, as expected.
Note. One doesn't need a tower of powers to observe bifurcation.
What is the value of $\,x^0\,$ for $\,x=0\,$? As a physicist by education, I would think that the limit of $\,x^0\,$ for $x\downarrow 0$ is
a bifurcation at $\,(x,y)=(0,1)\,$, as is clearly seen in the picture below.
Actually displayed are graphs of $y=x^{1/N}$ with $N\in\{\color{red}{-2,-4,-6,-8,-20},\color{blue}{+20,+8,+6,+4,+3}\,\}$.
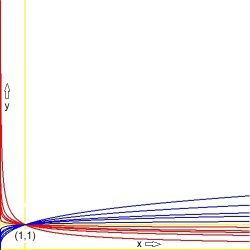
Formulated otherwise it would mean that $\,y=x^0=1\,$ is only defined for $\,x\gt 0\,$; it is not a function at $\,x=0\,$ and we have Commutativity of iterated limits: $$ \lim_{x\downarrow 0}\lim_{N\to\infty} \begin{cases} \color{blue}{x^{+1/N} = [0,1]} \\ \color{red}{x^{-1/N} = [1,\infty]} \end{cases} \\ \lim_{N\to\infty}\lim_{x\downarrow 0} \begin{cases} \color{blue}{x^{+1/N} = [0,1]} \\ \color{red}{x^{-1/N} = [1,\infty]} \end{cases} $$