Let $\,M \le N\,$ and
$X$ be a finite set of $N$ reals $x_i\,$: $X = \{x_1,x_2, .. ,x_i, .. ,x_N\}\,$,
$Y$ be a finite set of $M$ reals $y_j\,$: $Y = \{y_1,y_2, .. ,y_j, .. ,y_M\}\,$.
In order to determine whether $X$ is a subset of $Y$, we could compare the
elements: $X$ is a subset of $Y$, $\,X \subseteq Y\,$, if and only if for each of
the $\,x_i\,$ one of them is equal to $\,y_j\,$ :
$$
\quad ((x_1 = y_1) \vee (x_1 = y_2) \vee \cdots \vee (x_1 = y_j) \vee \cdots \vee (x_1 = y_M)) \\
\wedge ((x_2 = y_1) \vee (x_2 = y_2) \vee \cdots \vee (x_2 = y_j) \vee \cdots \vee (x_2 = y_M)) \\
\wedge \cdots \cdots \wedge \quad \\
\quad ((x_i = y_1) \vee (x_i = y_2) \vee \cdots \vee (x_i = y_j) \vee \cdots \vee (x_i = y_M)) \\
\wedge \cdots \cdots \wedge \quad \\
\quad ((x_N = y_1) \vee (x_N = y_2) \vee \cdots \vee (x_N = y_j) \vee \cdots \vee (x_N = y_M))
$$ $$
(X \subseteq Y) \Longleftrightarrow
\bigwedge_{i=1}^N \left[ \bigvee_{j=1}^M \left(x_i=y_j\right) \right]
$$
Because all $\,x_i\,$ and $\,y_j\,$ are real numbers, we can alsow write this
as follows; a product of terms is zero, if and only if one (or more)
of the factors is zero.
$$
(X \subseteq Y) \Longleftrightarrow
\bigwedge_{i=1}^N \left[ \prod_{j=1}^M \left(x_i-y_j\right) = 0\right]
$$
And each of the terms is zero if and only if the sum of the squares of
all of these terms is zero:
$$
(X \subseteq Y) \Longleftrightarrow
\sum_{i=1}^N \left[ \prod_{j=1}^M \left(x_i-y_j\right) \right]^2 = 0
$$
One can make this somewhat more computation friendly by implementing
products as geometric means: take the $M$-th root of each of the terms.
For the same reason, we shall implement the sum as an arithmetic mean.
Furthermore the above can easily be generalized to vectors $(\vec{x}_i,\vec{y}_j)$.
The we have at last, for the discrete case:
$$
(X \subseteq Y) \Longleftrightarrow
\sum_{i=1}^N \frac{1}{N} \left[ \prod_{j=1}^M \left|\vec{x}_i-\vec{y}_j\right|^2 \right]^{1/M} = 0
$$
In Wikipedia a definition is found of the Geometric Mean.
And there is a relationship with the arithmetic mean of logarithms at that page:
$$
{\displaystyle \left(\prod _{i=1}^{n}a_{i}\right)^{\frac {1}{n}}=\exp \left[{\frac {1}{n}}\sum _{i=1}^{n}\ln a_{i}\right];} \quad a_i > 0
$$
Together with the above then we have:
$$
(X \subseteq Y) \Longleftrightarrow
\sum_{i=1}^N \frac{1}{N} \exp\left[\frac{1}{M}\sum_{j=1}^M \ln(\left|\vec{x}_i-\vec{y}_j\right|^2)\right] = 0
$$
The following essential reading is needed, in order to be able to proceed.
Namely for converting the discrete into the continuous:
$$
(X \subseteq Y) \Longleftrightarrow
\int_0^1 \exp\left(\int_0^1 \ln(\left|\vec{x}(t)-\vec{y}(u)\right|^2)\,dt\right)\,du = 0
$$
where a minor detail is restriction to the integration interval $[0,1]$ by parameter transformation.
So far so good. Let's try now the simplest example possible, namely $\;\vec{x}(t)=t \; ; \; 0 \le t\le 1\;$ and
$\;\vec{y}(u)=u \; ; \; 0 \le u\le 1\;$.
Then it is clear that $(X=Y$ and so $(X \subseteq Y)$ and $(Y \subseteq X)$.
And our calculation effort is defined by proving that:
$$
\int_0^1 \exp\left(\int_0^1 \ln\left(|t-u\right|^2)\,dt\right)\,du
= \int_0^1 \exp\left(\int_0^1 \ln(\left|t-u\right|^2)\,du\right)\,dt = 0 \\
= \exp(-2)\int_0^1 u^{2u}(1-u)^{2(1-u)}\,du \approx 0.05378539284
$$
This is not by far the accuracy we did expect!
I think it has something to do with evaluating the logarithm for $t=u$ but I'm not sure. What precisely is going on?
Too long for a comment, in view of the (+1) answers by user937523 and 5xum.
While preparing the question, these were some of my notes:
$$
\int_0^1\ln(|y-x|^2)\,dx = 2\lim_{\delta\downarrow 0}\left[\int_0^{y-\delta} \ln(y-x)\,dx + \int_{y+\delta}^1 \ln(x-y)\,dx\right] = \\
2\lim_{\delta\downarrow 0} \left[-(y-x)\ln(y-x)+(y-x)\right]_{y-x=y}^{y-x=\delta} + \\
2\lim_{\delta\downarrow 0} \left[(x-y)\ln(x-y)-(x-y)\right]_{x-y=\delta}^{x-y=1-y} = \\
4\lim_{\delta\downarrow 0}\left[\,-\delta\ln(\delta)+\delta\,\right] + 2y\ln(y)-2y + 2(1-y)\ln(1-y)-2(1-y)
$$
And the limit between square brackets is zero, just because, indeed, the
The log function goes to $\pm \infty$ too "slowly" for the integral to diverge.
Furthermore, because of the condition $a_i > 0$, in the continuous case, we would have to consider instead the
Cauchy principal value for the singularity at zero
in the product integral / logarithm:
$$
\int_0^1 \exp\left(-\!\!\!\!\!\!\int_0^1 \ln(\left|\vec{x}(t)-\vec{y}(u)\right|^2)\,dt\right)\,du
$$
But the meaning of the latter is simply that we cannot calculate for being a subset in this way, because zero is essential as the outcome
and can never be obtained.
CGM of a straight line segment
It has been established that we cannot calculate for being a subset,
so the integral representing the arithmetic mean can safely be discarded.
Then we are left with the Cauchy principal value of a Continuous Geometric Mean:
$$
\operatorname{CGM}(\vec{r}) = \exp\left(-\!\!\!\!\!\!\int_0^1 \ln(\left|\vec{p}(t)-\vec{r}\right|^2)\,dt\right)
$$
where for example $\,\vec{p}(t)\,$ is a curve in the plane and $\,\vec{r}\,$ is a point in the plane.
For our straight line segment, we substitute:
$$
\vec{p}(t) = (t,0) \quad ; \quad \vec{r} = (x,y) \\
\operatorname{CGM}(x,y) = \exp\left(-\!\!\!\!\!\!\int_0^1 \ln\left|(t-x)^2+y^2\right| dt \right)
$$
A computer algebra system (MAPLE) has been employed for the purpose:
> int(ln((t-x)^2+y^2),t=0..1,continuous);
Giving that $\,\operatorname{CGM}(x,y) = e^{\Pi(x,y)}$ , with:
$$
\Pi(x,y) = (1-x)\ln(1-2x+x^2+y^2)+x\ln(x^2+y^2)-2 \\
+ 2y\left[\arctan\left(\frac{1-x}{y}\right)+\arctan\left(\frac{x}{y}\right)\right]
$$
The result has been programmed and when visualized it looks as follows:
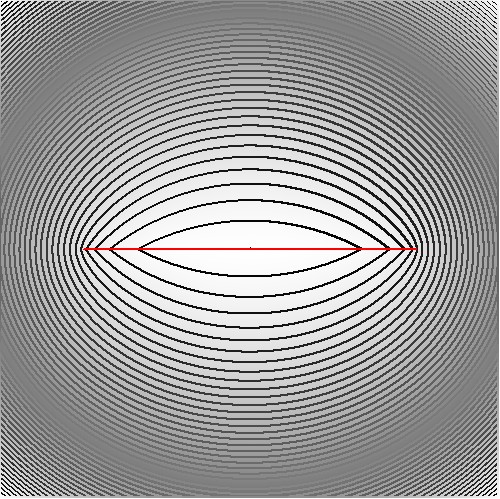
The lowest function values ($\approx 0.034$) are nearby the red line segment.
Window:
xmin := -0.25; xmax := +1.25; ymin := -0.75; ymax := +0.75;

