The first thing that must be done with $f(x)$ is to make it zero for $x=0$. Redefine:
$$
f^*(x)=\cases{1/\sqrt{\sinh^2(a)-\sinh^2(ax)}-1/\sinh(a) & $-1 \leq x \leq 1$ \\ 0 & otherwise}
$$
The next step is to divide it by the area underneath it.
With other words, $f^*(x)$ shall be normed, with a number called $N$:
$$
N(a) = \int_{-1}^{+1} f^*(x)\,dx = \int_{-1}^{+1} \left[\frac{1}{\sqrt{\sinh^2(a)-\sinh^2(ax)}}-\frac{1}{\sinh(a)}\right] dx
$$
Calculating the integral turns out to be a cumbersome job. It can hardly be done by hand.
Therefore we have invoked a computer algebra system, MAPLE to be precise:
> f(x,a) := 1/sqrt(sinh(a)^2-sinh(a*x)^2)-1/sinh(a);
> for k from 0 to 9 do evalf(int(subs(a=k+1,f(x,a)),x=-1..+1)) end do;
It is thus ensured that the area beneath the iterands $f^*(x)/N(a)$ is always unity.
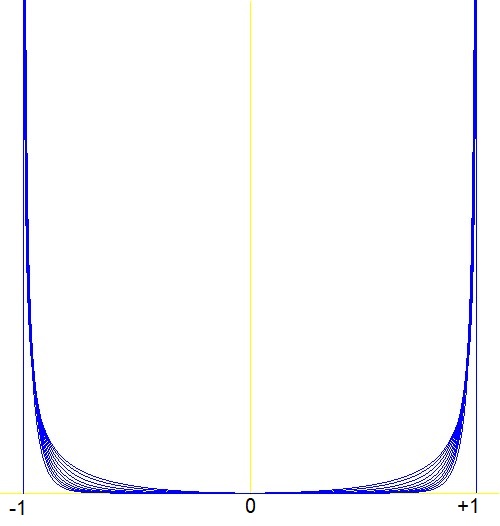
The numbers $N(a)$ have been plugged into a computer program. Here is a plot of the convergents of $f^*(x)$ for
parameter values $\,a=1\cdots 10\,$. Scaling is almost the same as in the OP's picture, but the $y$-axis has been elongated to $y \le 9.1$,
to demonstrate that the approximations do indeed "peak" near $x = \pm 1$.
The function is symmetric around $x=0$. It remains to be shown that:
$$ \begin{cases}
\lim_{a\to\infty} f^*(x = \pm 1)/N(a) = +\infty \\
\lim_{a\to\infty} f^*(x \ne \pm 1)/N(a) = 0
\end{cases} $$
Symbolically for the first case, because that limit does not really "exist".
But anyway the first case is trivial, because of the zero denominator.
The second case (a "true" limit) seems to be much more difficult.
Despite of the last technicality - to be repaired later eventually - we jump to conclusions:
$$
\lim_{a\to\infty} \frac{f^*(x)}{N(a)} = \frac{1}{2}\left[\,\delta(x+1)+\delta(x-1)\,\right]
$$
It is not possible to put this in a form as seems to be required in the question.
Later
In order to be able to proceed, we want to have an impression of the behaviour of the norming integral $N(a)$.
The problem is that $N(a)$ is a (too) quickly decreasing function, spoiling the party when trying to prove that
$\;\lim_{a\to\infty} f^*(x \ne \pm 1)/N(a) = 0\;$. Consider instead:
$$
N^*(a) = N(a)\,a\,e^a
$$
Our hope is that $\,N^*(a)\,$ is more or less a constant as a function of $a$.
Numerical experiments (with MAPLE) reveal that such indeed may be the case:
> f(x,a) := 1/sqrt(sinh(a)^2-sinh(a*x)^2)-1/sinh(a);
> for k from 0 to 19 do evalf(int(subs(a=k+1,f(x,a)),x=-1..+1)*(k+1)*exp(k+1),30) end do; evalf(ln(16),30);
Resulting in a sequence of numbers that seems to converge to $2.772588722239 \approx \ln(16)$.
Next consider the series expansion of $f^*(x)$ around $x=0$:
> series(f(x,a),x=0);
Resulting in:
$$
f^*(x) = \frac{1}{2}\frac{a^2}{\sinh(a)^3}x^2
+ \left[\frac{1}{6}\frac{a^4}{\sinh(a)^3} + \frac{3}{8}\frac{a^4}{\sinh(a)^5}\right]x^4 + O(x^6)
$$
For large $a > 0$ we know that $\,\sinh(a)\approx e^a\,$. Thus giving:
$$
f^*(x) \approx \frac{1}{2}a^2 e^{-3a}x^2 + \left[\frac{1}{6} a^4 e^{-3a} + \frac{3}{8} a^4 e^{-5a}\right]x^4 + O(x^6)
$$
Time to plug in our conjecturial approximation for the norming integral:
$$
\frac{f^*(x)}{N(a)} = \frac{f^*(x)}{N^*(a)}a\,e^a \approx \frac{a\,e^a}{\ln(16)} f^*(x) \approx \\
\frac{a^3 e^{-2a}}{2\ln(16)}x^2 + \left[\frac{a^5 e^{-2a}}{6\ln(16)} + \frac{3 a^5 e^{-4a}}{8\ln(16)}\right]x^4 + O(x^6)
$$
Which shows that $f^*(x)/N(a)$ is quickly (exponentially) decreasing to zero for $a\to\infty$ and $|x|\lt 1$,
the limit that was "to be repaired later" :-)
The finishing touch is provided with
contributions by DinosaurEgg and Claude Leibovici:
$\lim_{a\to\infty} N^*(a) = \ln(16)\;$ does indeed hold.
At last
This response is intended to provide a far more detailed heuristic account of the mathematical approach as employed by @DinosaurEgg in a previous
answer.
The function as prescribed in the question does not converge to a delta-function in the limit $a\to\infty$.
However it converges to one with appropriate modifications:
$$
f^*(x)=N(a)\left[\frac{1}{\sqrt{\sinh^2(a)-\sinh^2(ax)}}-\frac{1}{\sinh(a)}\right] \\
N(a) = \int_{-1}^{+1} \left[\frac{1}{\sqrt{1-\left[\,\sinh(ax)/\sinh(a)\,\right]^2}}-1\right]\frac{dx}{\sinh(a)}
$$
A good thing is performing the proposed change of variables:
$$
\sinh(ax)=\sinh(a)\tanh(t) \quad \Longrightarrow \\
\frac{1}{\sqrt{1-\left[\sinh(ax)/\sinh(a)\right]^2}} = \frac{1}{\sqrt{1-\tanh^2(t)}} \\
= \frac{1}{\sqrt{\left[\cosh^2(t)-\sinh^2(t)\right]/\cosh^2(t)}}=\cosh(t) \\
\cosh(ax)=\sqrt{1+\sinh^2(ax)}=\sqrt{1+\sinh^2(a)\tanh^2(t)}
$$
With implicit differentiation we get:
$$
h(x,t) = \frac{\sinh(ax)}{\sinh(a)}-\tanh(t) = 0 \quad \Longrightarrow \\
dh = \frac{\partial h}{\partial x}dx + \frac{\partial h}{\partial t}dt = a\frac{\cosh(ax)}{\sinh(a)}dx - \frac{1}{\cosh^2(t)}dt = 0
\quad \Longrightarrow \\ dx = \frac{dt}{a\cosh^2(t)\cosh(ax)/\sinh(a)}= \frac{\sinh(a)}{a}\frac{dt}{\cosh^2(t)\sqrt{1+\sinh^2(a)\tanh^2(t)}}
$$
Change of integration bounds:
$$
\tanh(-\infty)=-1 \quad ; \quad \tanh(+\infty)=+1
$$
It follows that:
$$
N(a) = \frac{1}{a}\int_{-\infty}^{+\infty} \frac{\left[\,\cosh(t)-1\,\right]dt}{\cosh^2(t)\sqrt{1+\sinh^2(a)\tanh^2(t)}} \\
= \frac{1}{a\sinh(a)}\int_{-\infty}^{+\infty} \frac{\left[\,\cosh(t)-1\,\right]dt}{\cosh^2(t)\sqrt{1/\sinh^2(a)+\tanh^2(t)}}
= \frac{1}{a\sinh(a)}N^*(a)
$$
By previous heuristics, it has been assumed that the following limit exists:
$$
\lim_{a\to\infty} N^*(a) = \int_{-\infty}^{+\infty} \lim_{a\to\infty} \frac{\left[\,\cosh(t)-1\,\right]dt}{\cosh^2(t)\sqrt{1/\sinh^2(a)+\tanh^2(t)}} \\
= \int_{-\infty}^{+\infty}\frac{\left[\,\cosh(t)-1\,\right]dt}{\cosh^2(t)\sqrt{\tanh^2(t)}} =
\int_{-\infty}^{+\infty}\frac{\left[\,\cosh(t)-1\,\right]dt}{\cosh^2(t)|\tanh(t)|}
$$
Take care of the absolute value $\,|\tanh(t)|\,$! This means that the integrand is symmetric in $t$, so we can write:
$$
\lim_{a\to\infty} N^*(a) = 2\int_0^\infty\frac{\cosh(t)-1}{\cosh(t)\sinh(t)}\,dt
$$
We could have asked MAPLE for some help:
> 2*int((cosh(t)-1)/(cosh(t)*sinh(t)),t=0..infinity);
And the outcome is quite in agreement wth our prediction (because of $\,\sinh(a) \to e^a/2\,$):
$$
\lim_{a\to\infty} N^*(a) = 2\ln(2) = \ln(16)/2
$$
But let us not be lazy and evalutate that last integral by hand.
Remember l'Hôpital's rule for the last part:
$$
\sinh(2t)=2\sinh(t)\cosh(t) \quad \quad \Longrightarrow \quad \sinh(t)=2\sinh(t/2)\cosh(t/2) \quad \Longrightarrow \\
\int_0^\infty\left[\frac{1}{\sinh(t)}-\frac{1}{\cosh^2(t)\tanh(t)}\right]dt = \\
\int_0^\infty\left[\frac{d(t/2)}{\tanh(t/2)\cosh^2(t/2)}-\frac{dt}{\tanh(t)\cosh^2(t)}\right]dt \\
= \left[\;\ln(\tanh(t/2))-\ln(\tanh(t))\;\right]_0^\infty = \left[\;\ln\left(\frac{\tanh(t/2)}{\tanh(t)}\right)\right]_0^\infty \\
= \ln\left(\lim_{t\to\infty}\frac{\tanh(t/2)}{\tanh(t)}\right) - \ln\left(\lim_{t\to 0}\frac{\tanh(t/2)}{\tanh(t)}\right) \\
= \ln(1)-\ln\left(\lim_{t\to 0}\frac{\tanh(t/2)}{\tanh(t)}\right)=-\ln\left(\lim_{t\to 0}\frac{(1/2)/\cosh^2(t/2)}{1/\cosh^2(t)}\right) \\
= -\ln(1/2)=\ln(2)
$$

