Maybe not exactly of the form that the OP has in mind, but working. Define $g(f,x)$ by:
$$
g(f,x) = \int_{-\infty}^{+\infty}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac12(x-t)^2/\sigma^2}\,f(t)\;dt
$$
Then we get the one-dimensional equivalent of Gaussian blur,
which causes $g(f,x)$ to be differentiable to $x$. For example:
$$
\frac{dg(f,x)}{dx} = \int_{-\infty}^{+\infty}-\frac{1}{\sigma\sqrt{2\pi}}\frac{x-t}{\sigma^2}e^{-\frac12(x-t)^2/\sigma^2}\,f(t)\;dt \\
\frac{d^2g(f,x)}{dx^2} = \int_{-\infty}^{+\infty}\frac{1}{\sigma\sqrt{2\pi}}\left[-\frac{1}{\sigma^2}+\frac{(x-t)^2}{\sigma^4}\right]e^{-\frac12(x-t)^2/\sigma^2}\,f(t)\;dt
$$
It also works for the Weierstrass function:
see Can monsters of real analysis be tamed in this way?.
EDIT. For differentiable functions $f$, partial integration shows consistency:
$$
g(f',x) = \int_{-\infty}^{+\infty}\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac12(x-t)^2/\sigma^2}\,\frac{df}{dt}\;dt = \\
\left[\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac12(x-t)^2/\sigma^2}\,f(t)\right]_{-\infty}^{+\infty}
+ \int_{-\infty}^{+\infty}f(t)\;d\left[\frac{1}{\sigma\sqrt{2\pi}}e^{-\frac12(x-t)^2/\sigma^2}\right] = \\
\int_{-\infty}^{+\infty}\frac{1}{\sigma\sqrt{2\pi}}\frac{x-t}{\sigma^2}e^{-\frac12(x-t)^2/\sigma^2}\,f(t)\;dt = \frac{dg(f,x)}{dx}
$$
Note that there are some technicalities involved with $f(t\to\pm\infty)$.
The effects of Gaussian blur may be visualized as follows.
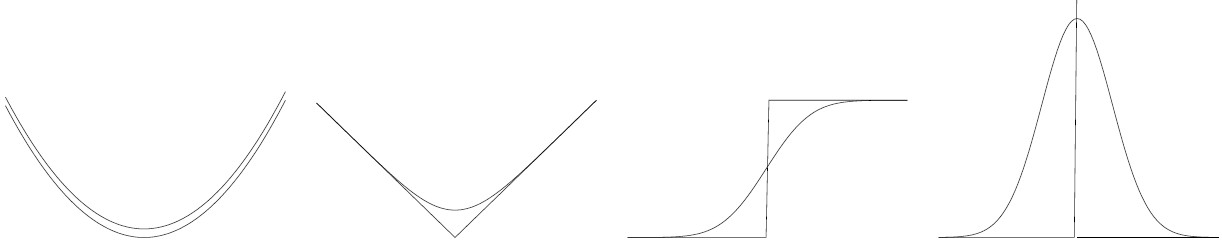
From the left to the right: parabola, the kink function $f(x)=|x|$, Heaviside function, Dirac delta.
Fuzzy Kinks
Imagine two arbitrary straight half-lines, which intersect each other at the
origin:
$$
\left[ \begin{array}{c} x_1(t) \\ y_1(t) \end{array} \right] = - t
\left[ \begin{array}{c} \cos(\alpha) \\ \sin(\alpha) \end{array} \right]
\qquad \mbox{for} \quad -\infty \lt t \le 0
$$ $$
\left[ \begin{array}{c} x_2(t) \\ y_2(t) \end{array} \right] = + t
\left[ \begin{array}{c} \cos(\beta) \\ \sin(\beta) \end{array} \right]
\qquad \mbox{for} \quad 0 \le t \lt +\infty
$$
The union of these two half-lines is a line-with-a-kink, which is to be studied
further:
$$
\left[ \begin{array}{c} x(t) \\ y(t) \end{array} \right] =
\left[ \begin{array}{c} x_1(t) \\ y_1(t) \end{array} \right] \cup
\left[ \begin{array}{c} x_2(t) \\ y_2(t) \end{array} \right]
$$
We are curious about the fuzzyfication of the kink (at the origin), which is
defined as follows:
$$
\int_{-\infty}^{+\infty} \frac{1}{\sigma \sqrt{2\pi}} \; e^{-\frac{1}{2} (t-\tau)^2/\sigma^2}
\left[ \begin{array}{c} x(\tau) \\ y(\tau) \end{array} \right] \; d\tau
\qquad \mbox{for} \quad t = 0
$$
Due to the above, this integral is equal to the sum of two parts:
$$
\frac{1}{\sigma \sqrt{2\pi}} \; \int_{-\infty}^0 e^{-\frac{1}{2} (t-\tau)^2/\sigma^2} \; (- \tau) \; d\tau
\cdot
\left[ \begin{array}{c} \cos(\alpha) \\ \sin(\alpha) \end{array} \right]
$$ $$
\; + \;
\frac{1}{\sigma \sqrt{2\pi}} \; \int_0^{+\infty} e^{-\frac{1}{2} (t-\tau)^2/\sigma^2} \; (+ \tau) \; d\tau
\cdot
\left[ \begin{array}{c} \cos(\beta) \\ \sin(\beta) \end{array} \right]
$$
Working out:
$$
\frac{1}{\sigma \sqrt{2\pi}} \; \int_{-\infty}^0 e^{-\frac{1}{2} (t-\tau)^2/\sigma^2} \; (-\tau) \; d\tau =
$$ $$
\frac{1}{\sigma \sqrt{2\pi}} \; \int_{-\infty}^0 e^{-\frac{1}{2} (t-\tau)^2/\sigma^2} \;
\frac{t-\tau}{\sigma^2} \; d\tau \; . \; \sigma^2 \quad - \quad
\frac{t}{\sigma\sqrt{2\pi}} \int_{-\infty}^0 e^{-\frac{1}{2} (t-\tau)^2/\sigma^2}
d\tau
$$
Substitute $u = - \frac{1}{2} (t-\tau)^2/\sigma^2$ into the first integral and
$v = (\tau-t)/\sigma$ into the second one, then $du = (t-\tau)/\sigma^2 d\tau$
and $u(0) = - \frac{1}{2} t^2/\sigma^2$ , $v(0) = - t/\sigma$ , giving:
$$
= \frac{\sigma}{\sqrt{2\pi}} \int_{-\infty}^{-\frac{1}{2} t^2/\sigma^2} e^u \;
d u \; . \; \sigma^2 \quad - \quad
t \cdot \int_{-\infty}^{-t/\sigma} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} v^2} d v =
$$ $$
\frac{\sigma}{\sqrt{2\pi}} e^{-\frac{1}{2} t^2/\sigma^2}
\; - t \, \operatorname{Erf}(-t/\sigma)
$$
Quite analogously:
$$
\frac{1}{\sigma \sqrt{2\pi}} \; \int_0^{+\infty} e^{-\frac{1}{2} (t-\tau)^2/\sigma^2} \; (+ \tau) \; d\tau
$$ $$
= - \frac{\sigma}{\sqrt{2\pi}} \int_{-\frac{1}{2} t^2/\sigma^2}^{-\infty} e^u \;
d u \; . \; \sigma^2 \quad + \quad
t \cdot \int_{-t/\sigma}^{+\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2} v^2} d v =
$$ $$
\frac{\sigma}{\sqrt{2\pi}} e^{-\frac{1}{2} t^2/\sigma^2}
\; + \; t \, \operatorname{Erf}(t/\sigma)
$$
Thus the general outcome is:
$$
\vec{\overline{r}}(t) =
\left\{ \frac{\sigma}{\sqrt{2\pi}} e^{-\frac{1}{2} t^2/\sigma^2}
\; - \; t \, \operatorname{Erf}(-t/\sigma) \right\}
\cdot
\left[ \begin{array}{c} \cos(\alpha) \\ \sin(\alpha) \end{array} \right]
$$ $$ +
\left\{ \frac{\sigma}{\sqrt{2\pi}} e^{-\frac{1}{2} t^2/\sigma^2}
\; + \; t \, \operatorname{Erf}(t/\sigma) \right\}
\cdot
\left[ \begin{array}{c} \cos(\beta) \\ \sin(\beta) \end{array} \right]
$$
It is seen that these expressions converge to the original straight half-lines
for $ | t | \gg \sigma$ . When specializing for $t = 0$ , we find:
$$
= \frac{\sigma}{\sqrt{2\pi}}
\left[ \begin{array}{c} \cos(\alpha) + \cos(\beta) \\
\sin(\alpha) + \sin(\beta) \end{array} \right]
$$
This expression can be simplified further by using a few goniometric formulas,
or even better by sketching an appropriate figure and using some elementary
geometry.
$$
\cos(\alpha) + \cos(\beta) =
2.\cos\left(\frac{\alpha+\beta}{2}\right).\cos\left(\frac{\alpha-\beta}{2}\right)
$$ $$
\sin(\alpha) + \sin(\beta) =
2.\sin\left(\frac{\alpha+\beta}{2}\right).\cos\left(\frac{\alpha-\beta}{2}\right)
$$
Giving for the fuzzyfied kink:
$$
\frac{\sigma}{\sqrt{2\pi}}\,.\,2\,.\,\cos\left(\frac{\alpha-\beta}{2}\right)
\left[ \begin{array}{c} \cos\left(\frac{\alpha+\beta}{2}\right) \\
\sin\left(\frac{\alpha+\beta}{2}\right) \end{array}
\right]
$$
This is a vector dividing the angle between the lines in two equal halves. And
its length is given by the astonishing simple formula:
$$
2\,.\,\cos(\phi/2) \frac{\sigma}{\sqrt{2\pi}}
$$
Where $\phi$ is the angle between the two half-lines.

