Disclaimer: this answer has a very limited scope to begin with.
Emphasis is on the method, which is solving for a polynomial equation of the form
$$
aB^N+bB^{N-1}+cB^{N-2}+ \cdots + xB^2+yB^1+zB^0=X
$$
For binary forms of size $2$ we trivially have, with $a\in\{0,1\}$ , $b\in\{0,1\}$ :
$$
aB^1+bB^0=X \quad \Longrightarrow \quad B = \frac{X-b}{a} \quad ; \quad a \ne 0 \\ \Longrightarrow
\begin{cases} ab = 10 & ; & B = X & ; & X = B \\ ab = 11 & ; & B=X-1 & ; & X = B+1 \end{cases}
$$
One step more complicated, for binary forms of size $3$ we have, with $a\in\{0,1\}$ , $b\in\{0,1\}$ , $c\in\{0,1\}$ :
$$
aB^2+bB^1+cB^0-X=0 \quad ; \quad a \ne 0 \\ \Longrightarrow \quad
B = \frac{-b \pm \sqrt{b^2-4ac}}{2a} \\ \Longrightarrow
\begin{cases}
abc = 100 & ; & B = \sqrt{X} & ; & X = B^2 \\
abc = 101 & ; & B = \sqrt{X-1} & ; & X = B^2+1 \\
abc = 110 & ; & B = \left[-1+\sqrt{1+4X}\right]/2 & ; & X = B^2 + B \\
abc = 111 & ; & B = \left[-1+\sqrt{1+4(X-1)}\right]/2 & ; & X = B^2 + B + 1
\end{cases}
$$
From this and the requirement that $X$ and $B$ must be integer, a number of examples can be derived, which is left as an exercise for the reader.
One other step more complicated.
For binary forms of size $4$ we have, with $a\in\{0,1\}$ , $b\in\{0,1\}$ , $c\in\{0,1\}$ :
$$
B^3+aB^2+bB+c=X
$$
Trying to solve for $\,B\,$ results in (computer) algebra you don't want to think about. Therefore I've decided to make a graph of the inverse of the polynomial,
which is a zillion times easier than to determine the inverse algebraically.
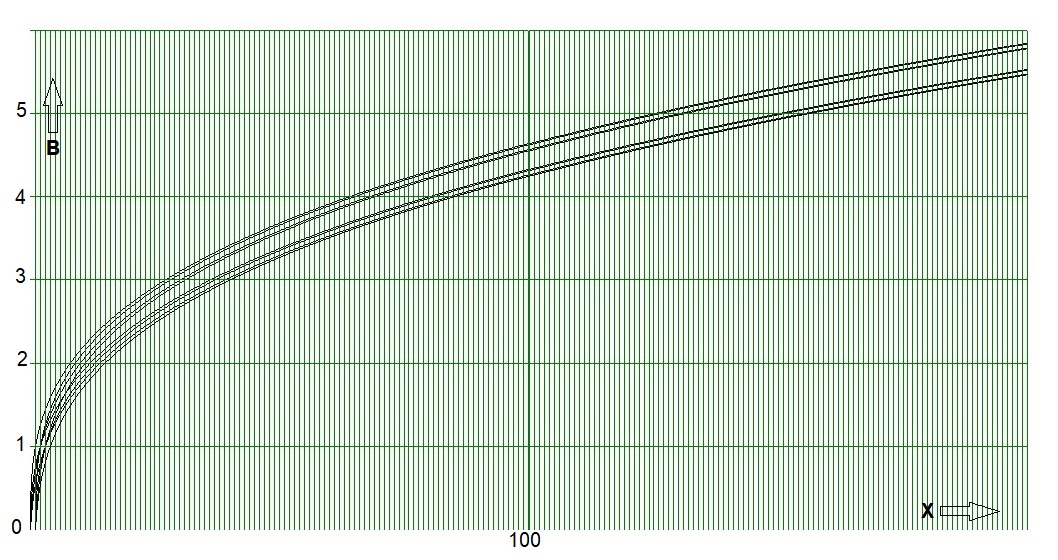
A few cases are noticed.
$$
\begin{cases}
B = 0 & \Longrightarrow & X = 0,1 \\
B = 1 & \Longrightarrow & X = 1,2,3,4 \\
B = 2 & \Longrightarrow & X = 8,9,10,11,12,13,14,15 \\
B = 3 & \Longrightarrow & X = 27,28,30,31,36,37,39,40
\end{cases}
$$
Continuing from there, the pattern becomes pretty boring.
Extending the method to $\,aB^N+bB^{N-1}+cB^{N-2}+ \cdots + xB^2+yB^1+zB^0=X\,$ seems prohibitive when done algebraically, and not very promising either.
Brute force approach
Free accompanying (Delphi Pascal) source code is available for this problem.
program later;
function binary(number,base : integer; var S : string) : boolean;
var
m : integer;
bit : byte;
OK : boolean;
begin
m := number; OK := true;
S := '';
while not (m = 0) do
begin
bit := (m mod base);
if bit = 1 then S := S + '1';
if bit = 0 then S := S + '0';
m := m div base;
if not ((bit=1) or (bit=0)) then OK := false;
end;
binary := OK;
end;
procedure reverse(var S : string);
var
k,L : integer;
c : char;
begin
L := Length(S);
for k := 1 to (L div 2) do
begin
c := S[k];
S[k] := S[L-k+1];
S[L-k+1] := c;
end;
end;
procedure for_number(X : integer);
var
k : integer;
S : string;
OK : boolean;
begin
{ for k := 2 to X do }
for k := 3 to X-2 do
begin
OK := binary(X,k,S);
if OK then
begin
reverse(S);
Writeln(X:5,k:5,S:10);
end;
end;
end;
procedure loop(N : integer);
var
K : integer;
begin
for k := 1 to N do
begin
for_number(k);
{ Writeln; }
end;
end;
begin
loop(100);
end.
In Pascal, comments are enclosed in curly brackets.
The commented for-do loop gives many trivial outcomes. Because of the base $2$ in the first place.
And, with a number $X$ every base $B$ with $B=X$ and $B=X-1$ will give rise to a binary, $10$ and $11$ respectively.
If we skip these most obvious trivialities, then the output becomes something like this. The first column is the number $X$, the second column is the base $B$ and the last column is the $(0,1)$ representation with base $B$.
9 3 100
10 3 101
12 3 110
13 3 111
16 4 100
17 4 101
20 4 110
21 4 111
25 5 100
26 5 101
27 3 1000
28 3 1001
30 3 1010
30 5 110
31 3 1011
31 5 111
36 3 1100
36 6 100
37 3 1101
37 6 101
39 3 1110
40 3 1111
42 6 110
43 6 111
49 7 100
50 7 101
56 7 110
57 7 111
64 4 1000
64 8 100
65 4 1001
65 8 101
68 4 1010
69 4 1011
72 8 110
73 8 111
80 4 1100
81 3 10000
81 4 1101
81 9 100
82 3 10001
82 9 101
84 3 10010
84 4 1110
85 3 10011
85 4 1111
90 3 10100
90 9 110
91 3 10101
91 9 111
93 3 10110
94 3 10111
100 10 100
