There is sloppyness in the question as well as in the
"proof"
mentioned in your comment.
But anyway, it's always wise to start with a special case if you can't cope immediately with the general problem.
So let's do the following.
$$
L(u) = a_{xx}\frac{\partial^2 u}{\partial x^2} + a_{xy}\frac{\partial^2 u}{\partial x \partial y}
+ a_{yx}\frac{\partial^2 u}{\partial y \partial x} + a_{yy}\frac{\partial^2 u}{\partial y^2}
+ b_x \frac{\partial u}{\partial x} + b_y \frac{\partial u}{\partial y}
$$
Then we subsequently have:
$$
h(x,y) = e^{-a(x^2+y^2)}-e^{-a(x_0^2+y_0^2)} \\
\frac{\partial h}{\partial x} = -2ax\,e^{-a(x^2+y^2)} \quad ; \quad
\frac{\partial h}{\partial y} = -2ay\, e^{-a(x^2+y^2)} \quad \Longrightarrow \\
\vec{\nabla} h = -2a\begin{bmatrix} x \\ y \end{bmatrix} e^{-a(x^2+y^2)}
$$
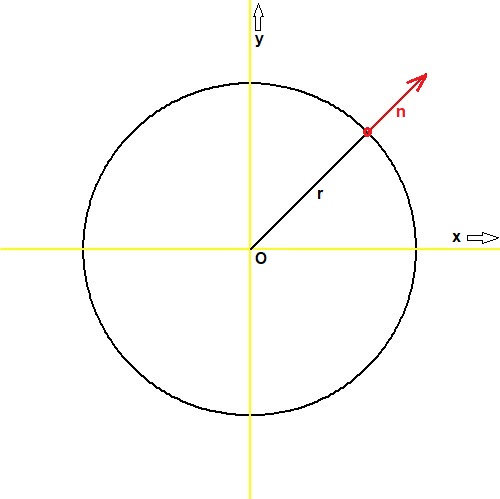
A hypersphere in two dimensions is a circle; the normal to the "surface" of a circle is
$\,\vec{n}=\begin{bmatrix} x & y \end{bmatrix}/\sqrt{x^2+y^2}$ ; and so the inner product is
$$
(\vec{\nabla} h \cdot \vec{n}) =
-2a \begin{bmatrix} x & y \end{bmatrix}/\sqrt{x^2+y^2}\begin{bmatrix} x \\ y \end{bmatrix}e^{-a(x^2+y^2)} =
-2a\,\sqrt{x^2+y^2}\,e^{-a(x^2+y^2)} \lt 0
$$
Which is indeed negative instead of positive. Proceeding with the second order derivatives:
$$
\frac{\partial^2 h}{\partial x^2} = \left[-2a + (-2ax)^2\right] e^{-a(x^2+y^2)} \\
\frac{\partial^2 h}{\partial y^2} = \left[-2a + (-2ay)^2\right] e^{-a(x^2+y^2)} \\
\frac{\partial^2 h}{\partial x \partial y} = (-2ax)(-2ay) e^{-a(x^2+y^2)} = \frac{\partial^2 h}{\partial y \partial y}
$$
And so for the "linear partial differential expression" we have:
$$
L(h) = \left[-2a(a_{xx}+a_{yy}+b_xx+b_yy) + 4a^2(a_{xx}x^2+a_{xy}xy+a_{yx}yx+a_{yy}y^2)\right]e^{-a(x^2+y^2)}
$$
Where it is noticed that there are additional terms for $x_i=x_k$ when compared with the analysis in your question.
But anyway, without additional resitrictions on $a_{ik}$ and $b_i$ it's difficult to see why $L(h)$ should be greater than 0.
Hope this helps. I do not understand the "proof" by Eberhard Hopf quite well.
EDIT.
The normal $\,\color{red}{\vec{n}}\,$ at a point of the surface of a hypersphere is the same as the vector towards that point $\,\vec{r}\,$,
apart from a norm. This is obvious for the two-dimensional hypersphere, called circle: