The easiest way is to start with considering the derivatives. Let $g(x)=f'(x)$. Then $g(x)$ must have an inverse $g^{-1}(x)$. This means that $y=g(x)$ is monotonically increasing or decreasing. $$ \mbox{Increasing:} \quad \begin{cases} x_1 \lt x_2 \quad \Longleftrightarrow \quad y_1 \lt y_2 \\ x_1 \gt x_2 \quad \Longleftrightarrow \quad y_1 \gt y_2 \end{cases} \\ \mbox{Decreasing:} \quad \begin{cases} x_1 \lt x_2 \quad \Longleftrightarrow \quad y_1 \gt y_2 \\ x_1 \gt x_2 \quad \Longleftrightarrow \quad y_1 \lt y_2 \end{cases} $$ The inverse $g^{-1}(x)$ is obtained (graphically) by mirroring $g(x)$ in the line $y=x$, thus by exchanging $x$ and $y$. From this it clear that $g(x)$ and $g^{-1}(x)$ must be both monotonically increasing or both be monotonically decreasing.
The same considerations are valid for $f(x)$ and $f^{-1}(x)$ as well, because these two are each others inverse too.
But $g(x)$ is also a derivative. If this derivative would become zero somewhere, then $f(x)$ would no longer be monotonic at that place. So $g(x)$ must be nonzero everywhere in its domain. For the inverse $g^{-1}(x)$ this means that there cannot be an intersection with the $y$-axis. Without loss of generality, we may assume that both $g(x)$ and $g^{-1}(x)$ are defined in the first quadrant, for $x \gt 0$ and $y \gt 0$. Other cases are covered by re-defining $g$ using symmetry: $g(x) := g(-x)$ , $g(x) := -g(x)$ , $g(x) := -g(-x)$.
Before proceeding, a few examples will be presented. First example: $$ f'(x) = g(x) = 1/x \quad ; \quad [f'(x)]^{-1} = g^{-1}(x) = 1/x \\ f(x) = \int_1^x\frac{dt}{t} = \ln(x) = y \quad ; \quad x = \ln(y) \; \Rightarrow \; f^{-1}(x) = e^x \quad ; \quad [f^{-1}]'(x) = e^x $$ It is noticed that $[f'(x)]^{-1}$ is monotonically decreasing while $[f^{-1}]'(x)$ is monotonically increasing. Second example: $$ f'(x) = g(x) = \sqrt{x} \quad ; \quad [f'(x)]^{-1} = x^2 \\ f(x) = \int_0^x\sqrt{t}\,dt = \frac{2}{3}x^{3/2} \quad ; \quad x = \frac{2}{3}y^{3/2} \; \Rightarrow \; f^{-1}(x) = \left(\frac{3x}{2}\right)^{2/3} \quad ; \quad [f^{-1}]'(x) = \left(\frac{3x}{2}\right)^{-1/3} $$ It is noticed that $[f'(x)]^{-1}$ is monotonically increasing while $[f^{-1}]'(x)$ is monotonically decreasing.
A pattern is emerging. Let's consider now the general case for $g(x)=f'(x)$ monotonically decreasing. It will be assumed that the reader is able to construct the analogue for monotonically increasing $g(x)$. Then $[f'(x)]^{-1}$ is monotonically decreasing as well. Define the function $f(x)$ as a definite integral in statu nascendi (a Riemann sum). For example as: $$ \sum_i g\left(x_i\right)\left(x_{i+1}-x_i\right) \approx \int_a^x g(t)\,dt = f(x) $$ And select the subdivisions in such a way that $$ g\left(x_i\right)\left(x_{i+1}-x_i\right) = \mbox{constant} = dA $$ Then we can construct the inverse function $f(x)$ by numerical approximation. It is clear thar if $g(x_i)$ is decreasing, then the area $dA$ can only kept constant by increasing the intervals $\left(x_{i+1}-x_i\right)$. This means that the intervals of $f^{-1}(x_i)$ must be increasing, because of $\left(x_{i+1}-x_i\right)\to\left(y_{i+1}-y_i\right)$. But then the derivative of $f^{-1}(x_i)$ is equal to $\left(y_{i+1}-y_i\right)/dA$, which means that $[f^{-1}]'(x)$ is increasing numerically, therefore analytically when taking limits. So here comes our end-result, apart from technicalities to filled in by the questioner eventually.

Theorem.
$[f'(x)]^{-1}$ is monotonically decreasing if and only if $[f^{-1}]'(x)$ is monotonically increasing.
$[f'(x)]^{-1}$ is monotonically increasing if and only if $[f^{-1}]'(x)$ is monotonically decreasing.
Therefore it is impossible to find (real valued) functions $f$ with $[f'(x)]^{-1}=[f^{-1}]'(x)$.

EDIT.

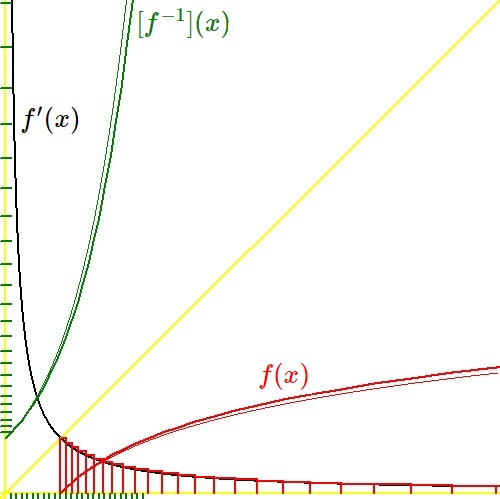
Below is a visualization of the technique employed, for the special example $f'(x)=[f'(x)]^{-1}=1/x$ , $\color{red}{f(x)=\ln(x)}$ , $\color{green}{f^{-1}(x)=[f^{-1}]'(x)=e^x}$ . Further specifications: $-0.1 \le x \le 9$ ; $-0.1 \le y \le 9$ ; $dA = 1/10$ ; thick colored lines numerically, thin colored lines analytically.

BUG FIX.

The domains of interest are much trickier than I thought.

Counter example. Consider $f(x)=1/x$, defined for $x\gt 0,y\gt 0$. Then $f'(x)=-1/x^2$ is defined for $x\gt 0,y\lt 0$; $[f'(x)]^{-1}=\sqrt{-1/x}$ is defined for $x\lt 0,y\gt 0$ and increasing; $f^{-1}(x)=1/x$ is defined for $x\gt 0,y\gt 0$; $[f^{-1}]'(x)=-1/x^2$ is defined for $x\gt 0,y\lt 0$ and increasing.
So we have a problem with the first two statements of our Theorem.

In general. Consider $f(x)$, defined for $x\gt 0,y\gt 0$ and monotonically decreasing. Then $f'(x)$ is defined for $x\gt 0,y\lt 0$ (i.e. negative) and monotonically increasing. $[f'(x)]^{-1}$, because of the mirroring in $y=x$, is defined for $x\lt 0,y\gt 0$ and monotonically increasing as well. $f^{-1}(x)$, because of the mirroring in $y=x$, is defined for $x\gt 0,y\gt 0$ and monotonically decreasing. So $[f^{-1}]'(x)$ is defined for $x\gt 0,y\lt 0$ and monotonically increasing.
However, because of the two different domains $[f^{-1}]'(x)$ cannot be identical to $[f'(x)]^{-1}$.
Conclusion: the last statement of our Theorem remains valid, but the first two statements, in general, are wrong.

Note. A better numerical approximation of the integral sometimes can be obtained with the trapezium rule: $$ \frac{g\left(x_i\right)+g\left(x_{i+1}\right)}{2}\left(x_{i+1}-x_i\right) = \mbox{constant} = dA = \frac{1}{n} $$ But it does work only if $g\left(x_{i+1}\right)$ can be predicted, given the value of $dA$. In case $g(x)$ is an orthogonal hyperbola, prediction is successful: $$ x_{i+1}-x_i=\frac{1}{n}\frac{2}{1/x_{i+1}+1/x_i}=\frac{1}{n}\frac{2x_{i+1}x_i}{x_{i+1}+x_i} \quad \Longleftrightarrow \\ n\left(x_{i+1}-x_i\right)\left(x_{i+1}+x_i\right)-2x_{i+1}x_i=nx_{i+1}^2-2x_ix_{i+1}-nx_i^2=0 \quad \Longleftrightarrow \\ x_{i+1} = \frac{x_i}{n}\pm\sqrt{\left(\frac{x_i}{n}\right)^2+x_i^2}\quad \Longrightarrow\quad x_{i+1}=x_i\left(\frac{1}{n}+\sqrt{1+\frac{1}{n^2}}\right) $$