Everything real-valued. Let $\vec{r} = (x,y)$ be the vector directed from the origin to a point at the perimeter of a circle.
Then the normal perpendicular to that perimeter at that point is $\vec{n} = \vec{r}/|\vec{r}|$.
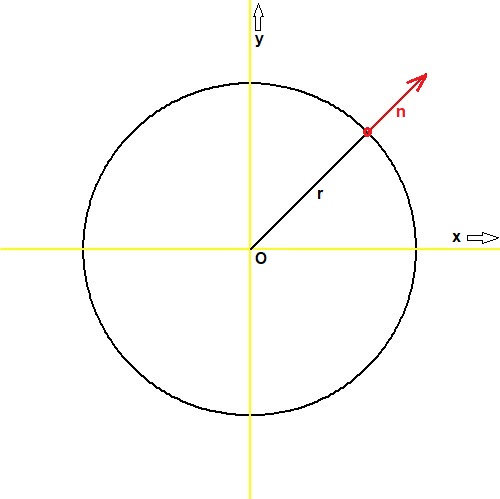
In very much the same way, the normal at the surface of a sphere is $\vec{n} = \vec{r}/|\vec{r}|$ with $\vec{r}=(x,y,z)$.
Question is: how is a normal at the surface of a hypersphere in n-dimensional space defined?
I would say, analogously to the
sphere and the circle, as follows:
$$
\vec{r} = (x_1,x_2,x_3, \cdots , x_n) \quad ; \quad \vec{n} = \frac{\vec{r}}{|\vec{r}|}
$$
But I haven't seen such a definition anywhere on the internet, for example with
N sphere , Unit sphere ,
Hypersphere .
Anyway, what is the surface of a hypersphere and how is a (normed) vector perpendicular to it defined?
Note. Motivated by a question elsewhere at MSE:
Problem with normal derivative.
According to Wikipedia,
and as formulated in the comment by Ben Grossmann, we can find the normal vector using the gradient of the function whose level set defines the surface.
For a hypersphere with radius $R$ that is:
$$
F(x_1,x_2,\cdots,x_n) = \left|\vec{r}\right|^2-R^2 = x_1^2 + x_2^2 + \cdots + x_n^2 - R^2 = 0
$$
And so, apart from a norming factor:
$$
\vec{n} =
\vec{\nabla} F = \left(\frac{\partial F}{\partial x_1},\frac{\partial F}{\partial x_2},\cdots,\frac{\partial F}{\partial x_n}\right) =
2\left(x_1,x_2,\cdots,x_n\right) = 2\,\vec{r}
$$

