Find the area enclosed by $\sqrt{(x-2)^2+(y-3)^2} + 2\sqrt{(x-3)^2+(y-1)^2} = 4$

Simple minded approach.
Take an area of $3500 \times 3500$ pixels (not really) and count the pixels inside the curve. 
DEPRECATED
VERY LATE UPDATE (2021).

Take an area of $3^{13} \times 3^{13}$ pixels (not really) and count the pixels inside the curve.
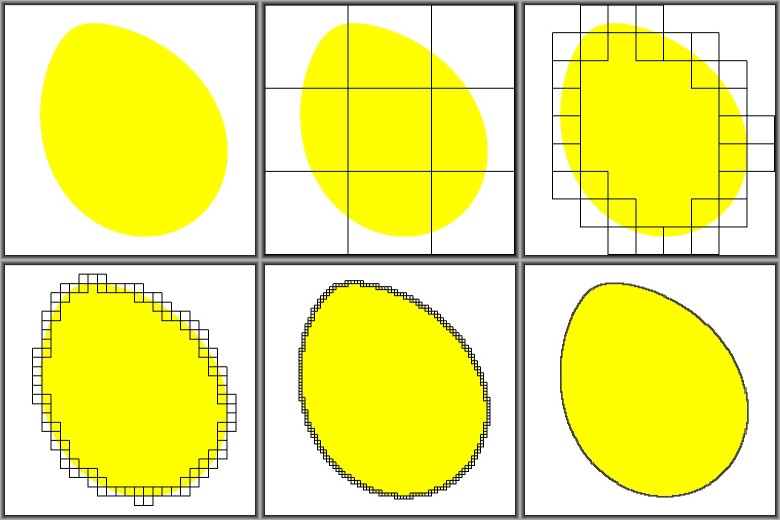
The following method is supposed to work for any convex closed (Jordan) curve that divides the plane.
Start with a grid of $3 \times 3$ squares and refine the grid three times each iteration.
Leave out a square as soon as all four vertices of it are guaranteed to be inside or outside the curve.
Continue (recursively) with the remaining squares, until the maximum grid refinement is reached.
Pictures say more that a thousand words:

Free accompanying (Delphi Pascal) source code available at this place:

Output after 13 iterations: $$ 3.204044 < \mbox{Area} < 3.204057 $$ Which is quite in agreement with (and inferior to) the above answer given by achille hui.
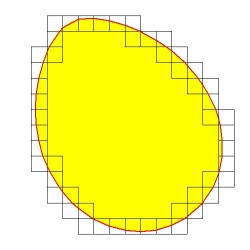
There is also a version available with binary instead of ternary refinement.
In addition, the software has been enhanced with Isoline Refinement. The meaning of the latter is best explained with a picture ($\color{red}{red}$ line):

With isoline refinement, a much better approximation of achille hui's result is found. Agreement is now within 12 digits. As a bonus, a value for the length of the perimeter is obtained as well: 

Area = 3.20405086915288E+0000
Perimeter = 6.457419618 86746E+0000