Let the equation of an ellipse in general be given by:
$$
Ax^2+Bxy+Cy^2+Dx+Ey+F=0
$$
Everything real valued, and well known it seems. But I have one question: how can we efficiently draw such an ellipse?
My attempt
I have a Delphi Pascal Unit at my disposal that does the Art
of Contouring. Simply calculate the isoline(s) of the function
$\,f(x,y)=Ax^2+Bxy+Cy^2+Dx+Ey+F\,$ at level zero: $\,f(x,y)=0\,$. One such result is shown in the picture below. I've been able
to reproduce in this way the outcome in an answer by Anders
Kaseorg to the question why a
Least square fit of ellipse worsens with increasing border thickness:
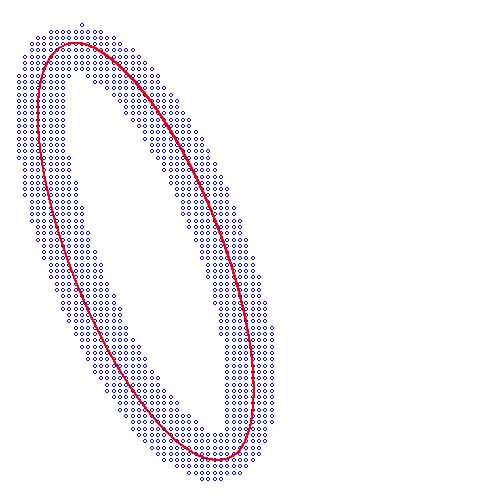
However, the Contouring method involves processing of all pixels in the canvas of a picture.
Computers are fast nowadays and there is plenty of memory available, so it may sound old fashioned,
but I find this method not very efficient. I wonder if there are better ways to do the drawing.
graphing-functions conic-sections
On one hand, we have the general equation for an ellipse:
$$
Ax^2+Bxy+Cy^2+Dx+Ey+F=0
$$
On the other hand, the following expression for an ellipse of inertia has been proposed
elsewhere:
$$
\frac{\sigma_{yy} (x-\mu_x)^2 - 2 \sigma_{xy} (x-\mu_x) (y-\mu_y)
+ \sigma_{xx} (y-\mu_y)^2}{ \sigma_{xx} \sigma_{yy} - \sigma_{xy}^2 } = 1
$$
The precise meaning of the coefficients is not important at this stage, as shown below.
Quoting from the accepted answer: First of all one must find the center of the ellipse.
For reasons of consistency (with the work called elsewhere) we put: $(x_O,y_O)=(\mu_x,\mu_x)$.
Consider:
$$
A(x-\mu_x)^2+B(x-\mu_x)(y-\mu_y)+C(y-\mu_y)^2 = \\
Ax^2-2A\mu_x x+A\mu_x^2 + Bxy-B\mu_x y-B\mu_y x+B\mu_x\mu_y + Cy^2-2C\mu_y y+C\mu_y^2 = \\
Ax^2+Bxy+Cy^2 + (-2A\mu_x-B\mu_y)x + (-2C\mu_y-B\mu_x)y + (A\mu_x^2+B\mu_x\mu_y+C\mu_y^2)
$$
This result must be compatible with: $Ax^2+Bxy+Cy^2+Dx+Ey+F$, so:
$$
\begin{cases}
2A\mu_x+B\mu_y = -D \\
B\mu_x+2C\mu_y = -E
\end{cases}
\quad \Longrightarrow \quad
\begin{bmatrix}
2C & -B \\ -B & 2A
\end{bmatrix} / (4AC-B^2)
\begin{bmatrix} \mu_x \\ \mu_y \end{bmatrix} =
\begin{bmatrix} -D \\ -E \end{bmatrix}
$$
The solution is in concordance with the the answer by Intelligenti pauca:
$$
\begin{bmatrix} \mu_x \\ \mu_y \end{bmatrix} =
\begin{bmatrix} 2CD-BE \\ 2AE-BD \end{bmatrix} / (B^2-4AC)
$$
Furthermore we have:
$$
Ax^2+Bxy+Cy^2+Dx+Ey+F = 0 \\
A(x-\mu_x)^2+B(x-\mu_x)(y-\mu_y)+C(y-\mu_y)^2 - (A\mu_x^2+B\mu_x\mu_y+C\mu_y^2) + F = 0 \\
\frac{A(x-\mu_x)^2 - 2(-B/2)(x-\mu_x)(y-\mu_y) + C(y-\mu_y)^2}{AC-(-B/2)^2} = \frac{A\mu_x^2+B\mu_x\mu_y+C\mu_y^2-F}{AC-(-B/2)^2}
$$
To be comparable with:
$$
\frac{\sigma_{yy} (x-\mu_x)^2 - 2 \sigma_{xy} (x-\mu_x) (y-\mu_y)
+ \sigma_{xx} (y-\mu_y)^2}{ \sigma_{xx} \sigma_{yy} - \sigma_{xy}^2 } = 1
$$
We are almost there. Define:
$$
\lambda = \frac{A\mu_x^2+B\mu_x\mu_y+C\mu_y^2-F}{AC-(-B/2)^2}
$$
Then we finally have:
$$
\frac{(\lambda A)(x-\mu_x)^2 - 2(-\lambda B/2)(x-\mu_x)(y-\mu_y) + (\lambda C)(y-\mu_y)^2}{(\lambda A)(\lambda C)-(-\lambda B/2)^2} = 1
$$
Cast into the ellipse of inertia format:
$$
\sigma_{yy} = \lambda A \quad ; \quad \sigma_{xy} = -\lambda B/2 \quad ; \quad \sigma_{xx} = \lambda C
$$
Now we can apply the method as described in Drawing an ellipse:
$$
\begin{cases}
x = \mu_x + a_x\cos(t) + a_y\sin(t) \\
y = \mu_y + b_x\cos(t) + b_y\sin(t)
\end{cases}
$$
With $(\mu_x,\mu_y)$ as defined above and:
$$
(a_x,a_y) = (\sqrt{\sigma_{xx}},0) \\
(b_x,b_y) = \left(\frac{\sigma_{xy}}{\sqrt{\sigma_{xx}}},\sqrt{\frac{\sigma_{xx}\sigma_{yy}-\sigma_{xy}^2}{\sigma_{xx}}}\right)
$$
Needless to say that the picture in the question can be exactly reproduced in this way.

