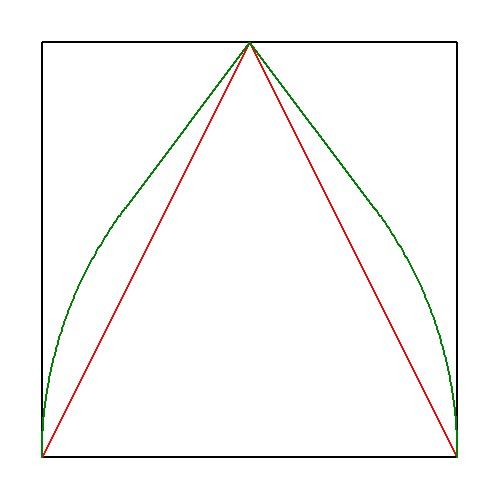
Not an answer but a pictorial comment.
Assuming a width of $1\,$, what's wrong then with a wire as sketched below?
EDIT.
Meanwhile, it has become clear that the minimum possible length of wire is meant in the question.
Okay. There is no shorter path between two points than a straight line, right? With symmetry, we have the following picture.
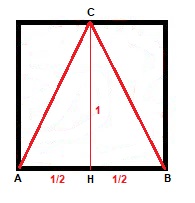
Assuming that the width (of the square) is again unity, we have for the length of the wire:
$$
\sqrt{\overline{AH}^2+\overline{HC}^2}+\sqrt{\overline{BH}^2+\overline{HC}^2}=
2\sqrt{\left(\frac{1}{2}\right)^2+1^2}=\sqrt{5}
$$
Which, according to the (+1) answer by fedja, is the optimum indeed.
The other way around we have wire length $=1$ and width $=1/\sqrt{5}\,$, a matter of scaling.
My updated solution does not have width $1$; if we measure along an axis perpendicular to one of the sides,
we find a width of $2/\sqrt{5}\approx 0.8944$.
Proof. Let the length of that perpendicular be $d$. It divides the side $\overline{BC}$ into pieces
$x$ and $(\sqrt{5}/2-x)$. Then with Pythagoras:
$$
\begin{cases}
1^2 = d^2 + (\sqrt{5}/2-x)^2 \\
(\sqrt{5}/2)^2 = d^2 + x^2 \end{cases} \\
1-(\sqrt{5}/2)^2=(\sqrt{5}/2-x)^2-x^2 \\
1-5/4=5/4-\sqrt{5}x+x^2-x^2 \\ x=\frac{10/4-1}{\sqrt{5}}=\frac{3/2}{\sqrt{5}} \\
d^2=(\sqrt{5}/2)^2-(3/2\sqrt{5})^2=5/4-9/20=16/20=4/5 \\
d = 2/\sqrt{5}
$$
The equation of the line along the side $\overline{BC}$ is:
$$
y-y_1=\frac{y_2-y_1}{x_2-x_1}(x-x_1) \\ y-0=\frac{1-0}{1/2-1}(x-1) \\ y=2(1-x)=-2x+2
$$
Intersection points with the circle $x^2+y^2=1$ are:
$$
x^2+(-2x+2)^2=1 \\
x^2+4x^2-8x+4=1 \\
5x^2-8x+3=0 \\
(x-1)(5x-3)=0 \\
\begin{cases} x=1 \\ y=0 \end{cases} \; \vee \; \begin{cases} x=3/5 \\ y = 4/5 \end{cases}
$$
But what is really interesting is the line through $(1/2,1)$ tangent at the circle:
$$
y-1=m(x-1/2) \; ; \; x^2+y^2=1 \quad \Longrightarrow \\
x^2+\left[1+m(x-1/2)\right]^2=1 \\
x^2+1+m^2(x-1/2)^2+2m(x-1/2)-1=0 \\
x^2+m^2x^2-m^2x+m^2/4+2mx-m=0 \\
(1+m^2)x^2+(-m^2+2m)x+(m^2/4-m)=ax^2+bx+c=0
$$
Normally, the line has two intersection points with the circle.
The line is tangent if these two points are the same,
which is the case if the two roots of the quadratic equation are equal,
that is if the discriminant is zero:
$$
b^2-4ac=(-m^2+2m)^2-4(1+m^2)(m^2/4-m)=0 \\
m^4+4m^2-4m^3-(m^2-4m+m^4-4m^3)=0 \\
3m^2+4m=m(3m+4)=0 \quad \Longrightarrow \\
m=0 \; \vee \; m=-4/3
$$
Giving with $\;a=1+m^2 \; ; \; b=-m^2+2m \; ; \; c=m^2/4-m\;$:
$$
\begin{cases} m=0 & \Longrightarrow \quad a=1 \; ; \; b=0 \; ; \; c=0 \\
m=-4/3 & \Longrightarrow \quad a=25/9 \; ; \; b=-40/9 \; ; \; c=16/9 \end{cases}
$$
Giving with $\; x=-b/2a \; ; \; y=1+m(x-1/2)\;$:
$$
\begin{cases} x=0 \\ y=1 \end{cases} \; \vee \; \begin{cases} x=4/5 \\ y = 3/5 \end{cases}
$$
Length of the tangent line $\;(1/2,1)-(4/5,3/5)\;$:
$$
\sqrt{(1/2-4/5)^2+(1-3/5)^2}=\sqrt{9/100+16/100}=5/10=1/2
$$
Length of the circle arc:
$$
\arctan(y/x)=\arctan(3/4)
$$
Numerical value:
> evalf(2*arctan(3/4)+1);
Giving a value of $\,2.2870\,$, to be compared with the somewhat more optimal $\,2.2783\,$ as calculated by the
questioner.