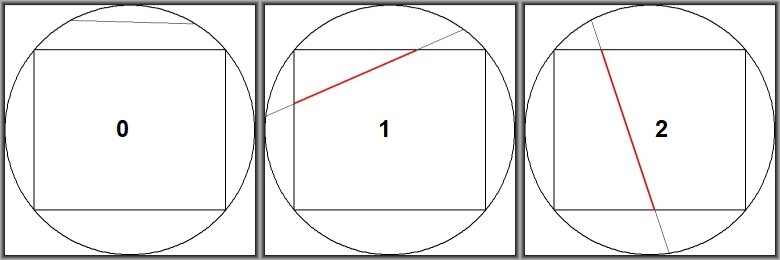
The rectangle has four corners, numbered as $(0,1,2,3)$.
The equation of a straight line divides the plane into a negative ( ≤ ) and a positive ( > ) region.
The line itself is the place where the equation equals zero ( ≤ ). Each of the corners of the rectangle
is in the negative ( ≤ ) or in the positive ( > ) region of the straight line.
A full solution of the problem requires that a number of different cases shall be distinguished.
A picture says more than a thousand words.
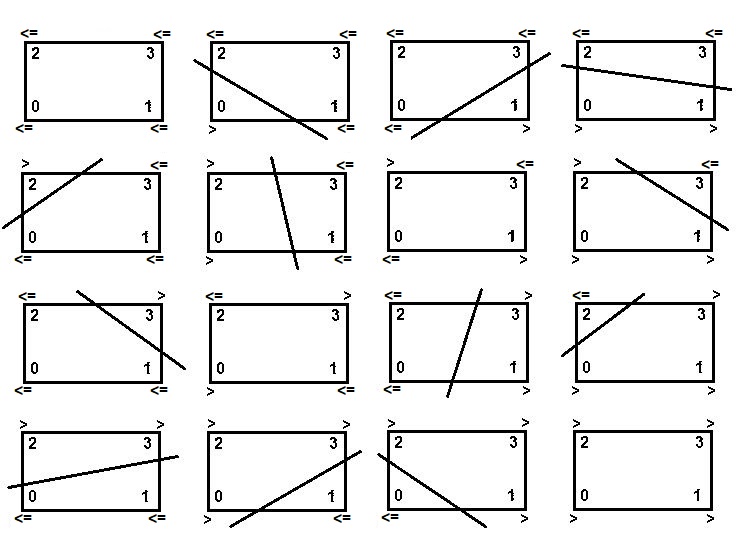
Mapping to the binary number system ensures that none of these sixteen cases will be omitted by accidence.
Employing symmetry, it turns out that the 16 cases can be collected into three classes.
binary 3 2 1 0 class
---------------------------
0 0000 ≤ ≤ ≤ ≤ 0
1 0001 ≤ ≤ ≤ > 1
2 0010 ≤ ≤ > ≤ 1
3 0011 ≤ ≤ > > 2
4 0100 ≤ > ≤ ≤ 1
5 0101 ≤ > ≤ > 2
6 0110 ≤ > > ≤ 0
7 0111 ≤ > > > 1
8 1000 > ≤ ≤ ≤ 1
9 1001 > ≤ ≤ > 0
10 1010 > ≤ > ≤ 2
11 1011 > ≤ > > 1
12 1100 > > ≤ ≤ 2
13 1101 > > ≤ > 1
14 1110 > > > ≤ 1
15 1111 > > > > 0
Now it's only a matter of finding the intersection of two lines for the classes (1) and (2), none for class (0).
Accompanying source code will be available at MSE publications / references 2021.
Here is some output, augmented with numbering of the 3 classes.