Define, with $x$ real valued:
$$
F_N(x) = \prod_{k=0}^N\left|x-\frac{k}{N}\right|^{1/N}
$$
We can calculate the limit for $N\to\infty$ as a Riemann sum converging to an integral:
$$
F_\infty(x) = \lim_{N\to\infty} \prod_{k=0}^N\left|x-\frac{k}{N}\right|^{1/N} = \\
\lim_{N\to\infty} \exp\left[\frac{1}{N}\sum_{k=0}^N\ln\left|x-\frac{k}{N}\right|\right] = \\
\exp\left[\int_0^1\ln|x-t|dt\right] \quad \Longrightarrow \\
F_\infty(x) = \exp\left[(x-1)\ln|x-1| + x\ln|x|-1\right]
$$
It can easily be shown that $\,F_\infty(0)=F_\infty(1)=1/e\,$ and there is a minimum for $\,F_\infty(1/2)=1/e/2\,$.
A graph says more than a thousand words:
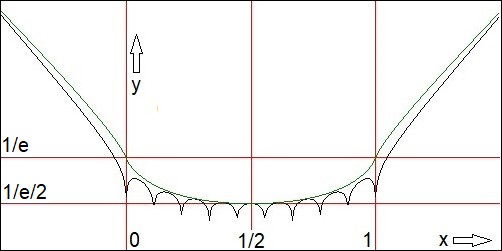
The interval $\,[0,1]\,$ and the minimum of $\,F_\infty\,$ are delimited with red lines.
A sample function $\,F_N(x)\,$ for $\,N=9\,$ is displayed in black. The limit function $\,F_\infty(x)\,$ is displayed in green.
Numerically it is suggested that the black curves $\,F_N\,$ converge to the green curve $\,F_\infty\,$.
With exception, though, of the function values $\,f_N(k/N)\,$; all of these must be zero from the start.
But in the limit this would mean that $\,F_\infty(x)\,$ is zero as well as non-zero at the whole $\,[0,1]\,$ interval.
Which is of course impossible.
What is a sensible way out of this dilemma?

