Derivation of bounds of convergence of infinite tower

The OP says: this of course can not be true.
But that's only for the power tower as such. What seems to have been considered instead, however, is the inverse function of the tower: $$ y = x^{x^{.^{.^{.^.}}}} = x^y \quad \Longrightarrow \quad x = y^{1/y} $$ Scaling in $y$-direction is three times scaling in $x$-direction in the picture below, for good reasons.

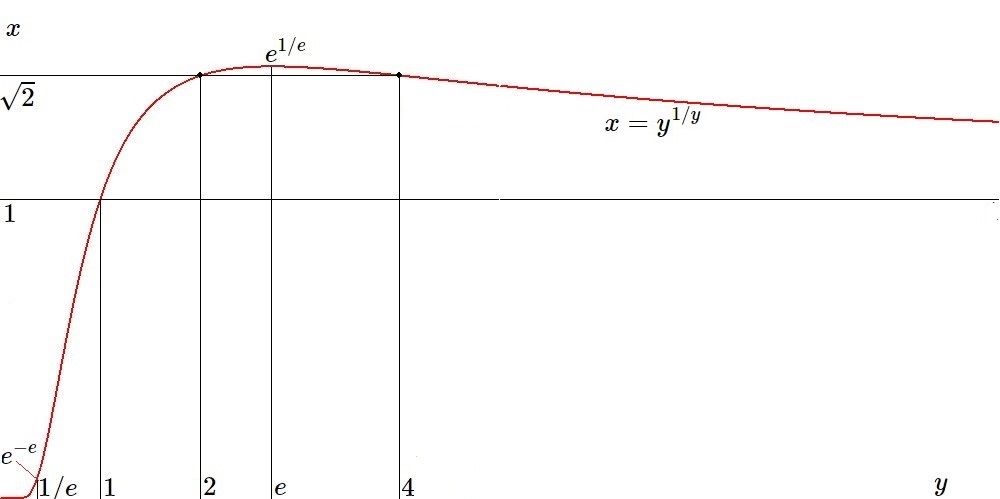
While the power tower itself is not defined outside the interval $e^{-e} \le x \le e^{1/e}$, the inverse function, when considered apart from the former, is defined, not only for $\,1/e \le y \le e\,$ but for a much larger domain, namely $\,0 \le y \lt \infty\,$. Details of function behaviour are described a great deal in the following MSE posting and its references:

It's easy to prove that $\,\lim_{y\to\infty} y^{1/y} = 1\,$. This means that $\,x = y^{1/y}\,$ has twofold solutions $\,y_{1,2}\,$ for $\,1 \lt x \lt e^{1/e}\,$, one $\,1 \lt y_1 \lt e\,$ and the other $\,e \lt y_2\,$, wich is anyway clear from the picture. Indeed the OP's solutions are among these: $\,1 \lt 2\lt e \lt 4\,$.
Numerically. Solutions of $\,y^{1/y}=x\,$ have been calculated by the (Delphi Pascal) program below. Values of $\,x\,$ are taken from a sample array, giving accompanying $\,y_{1,2}\,$ values with Newton's method. Initial $\,y_{1,2}\,$ are taken from previous steps, starting with the two known values from the question. 
program edit;

function Newton(y12,x : double) : double;
const
  eps : double = 1.e-9;
var
  y : double;
begin
  y := y12;
  while abs(exp(ln(y)/y)-x) > eps do
    y := y - (exp(ln(y)/y)-x) * sqr(y)/(exp(ln(y)/y)*(1-ln(y)));
  Newton := y;
end;

procedure test;
const
  x : array[0..8] of double =
 (1.4, 1.3, 1.2, 1.1, 1.05, 1.02, 1.01, 1.001, 1.0001);
var
  y1,y2 : double;
  k : integer; 
begin
  y1 := 2; y2 := 4;
  for k := 0 to 8 do
  begin
    y1 := Newton(y1,x[k]);
    y2 := Newton(y2,x[k]);
    Writeln(x[k],' ==> (',y1,',',y2,')');
  end;
end;

begin
  test;
end.
Output: 
 1.40000000000000E+0000 ==> ( 1.88666330624630E+0000, 4.41029279309327E+0000)
 1.30000000000000E+0000 ==> ( 1.47098895928257E+0000, 7.85706535100170E+0000)
 1.20000000000000E+0000 ==> ( 1.25773454121357E+0000, 1.47674583809828E+0001)
 1.10000000000000E+0000 ==> ( 1.11178201104165E+0000, 3.82287327653121E+0001)
 1.05000000000000E+0000 ==> ( 1.05270345488064E+0000, 9.28715283791938E+0001)
 1.02000000000000E+0000 ==> ( 1.02041238660200E+0000, 2.85536314597273E+0002)
 1.01000000000000E+0000 ==> ( 1.01010152374054E+0000, 6.51100334614211E+0002)
 1.00100000000000E+0000 ==> ( 1.00100100150234E+0000, 9.12312634995737E+0003)
 1.00010000000000E+0000 ==> ( 1.00010001000084E+0000, 1.16676997475209E+0005)
It is seen that the $\,y_1\,$ values near $\,y=1\,$ are close to $\,x\,$. Which should not be surprising, because $1^{1/1}=1$ and $\,\left. dx/dy\right|_{y=1}=1\,$. But I have no decent estimate for the "far away" solutions $\,y_2\,$.
By substituting $u=1/y$ the function $x=y^{1/y}$ is mapped onto $x=u^{−u}$. Which has a value $1$ for $u\to 0$ and a derivative $dx/du(u\to 0)\to\infty$. The latter is a measure for the error in the outcomes for $u\to 0$ i.e. $y\to \infty$. This makes me think that there does not exist any decent approximation for the "far away" $y_2$ values.