program apart;

procedure test(r : double; eps : double);
var
  a : double;
  m,n : integer;
begin
  a := 1;
  m := 0; n := 0;
  while true do
  begin
    if a < r then
    begin
      m := m + 1;
      a := a * 2;
    end else begin
      n := n + 1;
      a := a / 3;
    end;
    if abs(r-a) < eps then Break;
  end;
  Writeln(r,' = 2^',m,'/3^',n,' =',a);
end;

begin
  test(sqrt(2),1.E-3);
end.

 1.41421356237310E+0000 = 2^243/3^153 = 1.41493657935359E+0000

Note. The question can also be formulated as: Can any positive real be approximated as $3^m/2^n$ with $(m,n)$ large enough? Which is the same as allowing negative integers with the original formulation. In this form, it shows some resemblance to the (in)famous Collatz problem.

EDIT.
As suggested by the answers, an approach with logarithms could be more effective:

program anders;

procedure proef(r : double; eps : double);
var
  a,l2,l3,lr : double;
  m,n : integer;
begin
  l2 := ln(2); l3 := ln(3);
  lr := ln(r); a := 0;
  m := 0; n := 0;
  while true do
  begin
    a := m*l2 - n*l3 - lr;
    if abs(a) < eps then Break;
    if a < 0 then m := m + 1 else n := n + 1;
  end;
  Writeln(r,' = 2^',m,'/3^',n,' =',exp(a)*r);
end;

begin
  proef(sqrt(2),1.E-3);
  proef(sqrt(2),1.E-9);
end.

 1.41421356237310E+0000 = 2^243/3^153 = 1.41493657935356E+0000
 1.41421356237310E+0000 = 2^911485507/3^575083326 = 1.41421356125035E+0000

Continuing story at:
Can the Stern-Brocot tree be employed for better convergence of $2^m/3^n$?

Heuristics of a another proof

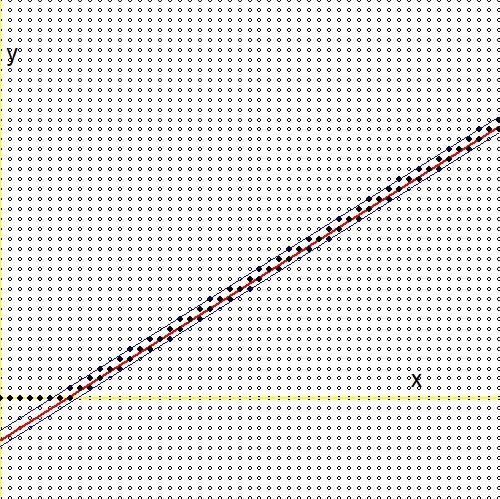
So what we have is a bunch of fractions, all different, but they must fit within the interval $\,]r/3,2r[\,$. This means that the fractions become crowded. Let's make a picture of the iteration process, logarithmic version. The red line is given by $\,\color{red}{\ln(3)y=\ln(2)x-\ln(r)}\,$, small circles are fractions, mapped on a grid $\,m/n \to (m,n)\,$, massively black filled dots are the fractions in the iteration process, while increasing $m$ and $n$ with increments one at a time. The iterations domain is limited by: $\,\color{blue}{-\ln(2)\lt\ln(3)y-\ln(2)x+\ln(r)\lt\ln(3)}\,$. In our case $r = 100$. Mind the sequence at the start.

So it seems that there must be quite some fractions nearby the red line, rerpesenting the real number $r$ in question.
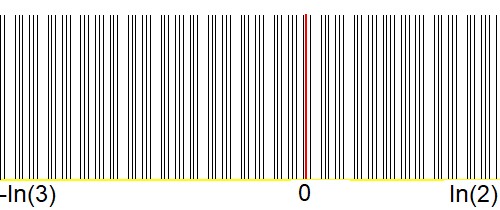
How can we be sure about this? Let's make picture of the crowding of the approximations $a$ in the interval $\,]r/3,2r[\,$, logarithmic scale: $$ a = m\ln(2)-n\ln(3)-\ln(r) \quad \mbox{with} \quad -\ln(3) < a < \ln(2) $$ The red line is where $a = 0$, the desired value.

Further numerical/graphical experiments reveal that the distribution of the fractions seems to be uniform. While seeking further confirmation of this we have done the following, speaking in terms of (Delphi) Pascal:

program opnieuw;

procedure interval(var A,B : double);
var
  h : double;
begin
  A := Random; B := Random;
  if A > B then
  begin
    h := B; B := A; A := h;
  end;
end;

procedure proef(r : double);
const
  veel : integer = 1000000000;
var
  x,l2,l3,lr,A,B : double;
  m,n,tel,t : integer;
begin
  l2 := ln(2); l3 := ln(3);
  lr := ln(r);
  interval(A,B);
  A := -l3 + A*(l2+l3);
  B := -l3 + B*(l2+l3);
  m := 0; n := 0;
  tel := 0; t := 0;
  while tel < veel do
  begin
    x := m*l2 - n*l3 - lr;
    if x < 0 then m := m + 1 else n := n + 1;
    if (-l3 < x) and (x < +l2) then tel := tel + 1;
    if (A < x) and (x < B) then t := t + 1;
  end;
  Writeln((B-A)/(l2+l3),' = ',t/tel);
end;

begin
  Random; Random;
  proef(1000);
  proef(0.001);
  proef(sqrt(2));
  proef(1/sqrt(2));
  while true do
    proef(Random);
end.

 6.58467502100393E-0001 =  6.58467500000000E-0001
 3.98733151378110E-0001 =  3.98733149000000E-0001
 1.56895805848762E-0001 =  1.56895804000000E-0001
 5.34354087430984E-0002 =  5.34354050000000E-0002
 4.04224734520540E-0001 =  4.04224734000000E-0001
 2.33572337077931E-0001 =  2.33572341000000E-0001
 4.06758418539539E-0001 =  4.06758418000000E-0001
 1.46495995344594E-0001 =  ....