Renormalization by Fuzzyfication
The End of Renormalization?

Firm disclaimer. Please don't expect a revolutionary new kind of mathematics to be employed by this author. The mathematics employed here is actually very conventional. And rather simple as well. The only thing that may be labeled as new is an entirely different interpretation of the same, well-known physical and mathematical facts.

Quantum Electrodynamics

Work in Progress

The Top Down Approach

Renormalization of Singularities

Fluid Tube Continuum

Prime Number Theory

This is the ground breaking paper by Richard P. Feynman: 'Space-Time Approach to Quantum Electrodynamics'

To be honest, I can read such a paper as if it is a novel, written in French. Now I cannot really speak French, but I can at least understand a bit of what they are saying, if they are prepared to pronounce slowly. And that turns out to be difficult: "Lentement, s'il vous plait, très lentement."
Well, everybody has his specialism. And Quantum ElectroDynamics (QED) certainly is not mine. Why then this attempt to nevertheless say some sensible things about it? To our great relief, the following sentence appears in Feynman's paper, quote from chapter 5:

We desire to make a modification of quantum electrodynamics analogous to the modification of classical [OK !] electrodynamics described in a previous article, A. There the δ(s₁₂²) appearing in the action of interaction was replaced by f(s₁₂²) where f(x) is a function of small width and great height.

Further support of this idea is found in the very well readable

Richard P. Feynman - Nobel Lecture :

There were several suggestions for interesting modifications of electrodynamics. We discussed lots of them, but I shall report on only one. It was to replace this delta function in the interaction by another function, say, f(I²_ij), which is not infinitely sharp. Instead of having the action occur only when the interval between the two charges is exactly zero, we would replace the delta function of I² by a narrow peaked thing. Let's say that f(Z) is large only near Z=0 width of order a². Interactions will now occur when T²-R² is of order a² roughly where T is the time difference and R is the separation of the charges. This might look like it disagrees with experience, but if a is some small distance, like 10^-13 cm, it says that the time delay T in action is roughly √ (R² ± a²) or approximately, - if R is much larger than a, T = R ± a²/2R. This means that the deviation of time T from the ideal theoretical time R of Maxwell, gets smaller and smaller, the further the pieces are apart. Therefore, all theories involving in analyzing generators, motors, etc., in fact, all of the tests of electrodynamics that were available in Maxwell's time, would be adequately satisfied if were 10^-13 cm. If R is of the order of a centimeter this deviation in T is only 10^-26 parts. So, it was possible, also, to change the theory in a simple manner and to still agree with all observations of classical electrodynamics. You have no clue of precisely what function to put in for f, but it was an interesting possibility to keep in mind when developing quantum electrodynamics.

It is noted that much of this classical electrodynamics theory is also found in 'The Feynman Lectures on Physics' Part II, chapter 28: 'Electromagnetic mass'. In paragraph 28-5, which is titled 'Attempts to modify the Maxwell theory' we read (at page 28-8) about 'another modification of the laws of electrodynamics as proposed by Bopp'. Bopp's theory is that:   A_μ(1,t₁) = ∫ j_μ(2,t₂) F(s₁₂²) dV₂ dt₂
It's important to observe that the above integral has all characteristics of a convolution integral with F as a kernel.You may forget all the rest, but remember this !
Subsequent quotes are aimed at showing that Feynman actually did copy the method "with δ replaced by a function of small width and great height", from classical electrodynamics to quantum electrodynamics:

Anyway, it forced me to go back over all this and to convince myself physically that nothing can go wrong. At any rate, the correction to mass was now finite, proportional to ln(m.a/h) (where a is the width of that function f which was substituted for δ). If you wanted an unmodified electrodynamics, you would have to take a equal to zero, getting an infinite mass correction. But, that wasn't the point. Keeping a finite, I simply followed the program outlined by Professor Bethe and showed how to calculate all the various things, the scatterings of electrons from atoms without radiation, the shifts of levels and so forth, calculating everything in terms of the experimental mass, and noting that the results as Bethe suggested, were not sensitive to a in this form and even had a definite limit as a → 0.
[ ... snip ... ]
It must be clearly understood that in all this work, I was representing the conventional electrodynamics with retarded interaction, and not my halfadvanced and half-retarded theory corresponding to (1). I merely use (1) to guess at forms. And, one of the forms I guessed at corresponded to changing δ to a function f of width a², so that I could calculate finite results for all of the problems. This brings me to the second thing that was missing when I published the paper, an unresolved difficulty. With δ replaced by f the calculations would give results which were not "unitary", that is, for which the sum of the probabilities of all alternatives was not unity. The deviation from unity was very small, in practice, if a was very small. In the limit that I took a very tiny, it might not make any difference. And, so the process of the renormalization could be made, you could calculate everything in terms of the experimental mass and then take the limit and the apparent difficulty that the unitary is violated temporarily seems to disappear. I was unable to demonstrate that, as a matter of fact, it does.

That was in 1965. Since then, a zillion proposals have been done to get rid of the "infinities" in Quantum Electrodynamics. Shall we summarize the situation?

But, some people seemingly succeed in keeping sort of order in the chaos. People such as John Baez. He has written many lucid articles on Mathematical Physics, this one for example:

Renormalization Made Easy (but where is it?)

We are talking here about the "oldest game", which is Feynman's game. A rather new development is the approach via "renormalization groups" by Kenneth Wilson (1982). Giving rise, again, to an interesting quote:

Wilson's analysis takes just the opposite point of view, that any quantum field theory is defined fundamentally with a distance cutoff D that has some physical significance. In statistical mechanical applications, this distance scale is the atomic spacing. In quantum electrodynamics and other quantum field theories appropriate to elementary particle physics, the cutoff would have to be associated with some fundamental graininess of spacetime, [ ... snip ... ] But whatever this scale is, it lies far beyond the reach of present-day experiments. Wilson's arguments show that this this circumstance explains the renormalizability of quantum electrodynamics and other quantum field theories of particle interactions. [ ... snip ... ]

There is also a popularized version of Quantum ElectroDynamics theory: Feynman's book 'QED: The Strange Theory of Light and Matter'.

• Even the slightest deviation of exact physics may give rise to a convolution integral with a broadened delta-function as a kernel. This is exemplified in Fuzzy Optics, where a sharp picture formed by standard Geometrical Optics becomes fuzzyfied, by shifting the plane of image formation slightly out-of-focus.
  (This work is not perfect yet. Improvements have been suggested by Robert Low, as seen in a subtread of 'Probability in an infinite sample space': 1 , 2 , 3 , 4 , 5 )

• There has been the (2004) article in 'sci.math' that a delta function can be conceived indeed as the limiting shape of a Gauss distribution function. And we can work, of course, the other way around: Airy R. Bean's Problem.

• The other way around may be conventionally called fuzzyfication or smoothing or broadening, as opposed to sharpening. Working back and forth between the sharp and the fuzzy picture has been done in i.e. Inside/Outside Problem and, apparently, may give rise to new insights.

• With fuzzyfication, it's quite possible to replace the Gaussian distribution by some other function "of small width and great height". But there are some good reasons why the Gaussian is my absolute favorite. One of the reasons being the following nice heuristics: The Normal Distribution: A derivation from basic principles.

• Fuzzyfied Differential Geometry and Fuzzyfied Lissajous Analysis has resulted in some interesting mathematics. Such as a wonderful formula for the fuzzyfication of a kink (a \/ like in f(x) = |x| ): the maximal distance between the original and the fuzzyfication is   2 cos(φ/2) σ/√(2π) , where φ = angle and σ = spread.

• Our Fuzzyfied Differential Geometry starts with a subsection 'Subsequent Fuzzyfications'. Here it is established (for a special case) that the spreads of subsequent fuzzyfications add op in a Pythagorean sense. Meaning that we are finished by considering the smoothing of a piece of mathematics only once in a lifetime.

• Our favorite derivation of the Laplace Transform is in 'Re: Why exp(-st) in the Laplace Transform?'. (More about operator calculus in a 'sci.math' article)
  In the same document, a result is established which is quite relevant here: Gaussian Smoothing is represented by an operator  exp( 1/2 σ² d/dx² )

• The Gaussian broadening operator explains why, as a first approximation, any fuzzyfied differentiable function is approximately equal to the original, plus a half times the square of the spread times the second order derivative. If the spread is to be interpreted as an infinitesimal in SIA (: see below), then the difference between the fuzzyfication and the original cannot even be observed. With fuzzyfied curves, the second order derivative must be replaced by the curvature.

  The effects of Gaussian broadening may be visualized as follows.

• But the Gaussian is not by far the only "broadening operator" in existence. A dozen others have been derived a long time ago, as is seen in the document 'Heaviside Operational Rules Applicable to Electromagnetic Problems'. Corresponding with the fact that there exist many such "functions of small width and great height".

• It is evident from Heaviside's work that broadening operators of the kind always commute with differential operators where the coefficients are constants. This means that - apart from any boundary conditions - "smoothed" functions are expected to be solutions of the governing differential equations as well.

• Gaussian broadening makes even a staircase to look like if it is ia smooth function. In two dimensions, the idea can be applied to black & white pixel pictures, resulting in a slightly blurred, but continuous representation, which then can be easily transformed (rotated, skewed) by the inverse transformation of coordinates.

• It's a small step from staircase functions to discrete functions. With Gaussian smoothing, it's quite easy to transform a discrete problem into a continuous counterpart. As has been demonstrated with an excercise on Numerical Differentiation. I do not claim that this is a very "efficient" way to do it, but it's evident that it works.

• In the 'Fuzzy Analysis' paper, there is also the theorem that the integral over a fuzzyfied function is equal to the integral over the original. This seems to imply that renormalization doesn't help against divergent integrals. But it rather means that renormalization can be accomplished only by fuzzyfication of the primitive function.

• A noteworthy by-product of numerical differentiation with help of Gaussian "interpolations" is that functions, fuzzyfied in this way, are analytical: differentiable, but infinitely often. This is quite in agreement with the fact that, in i.e. physics, "neat" functions are employed most of the time.

• In the documentation, it is also demonstrated hat sort of a 'Sampling Theorem' is valid for Gaussian smoothing. This effectively means that a discrete substrate cannot be recovered from the continuization if the discretization's spacing is less than half the spread of the broadening kernel. Quite analogous to Shannon's Theorem.

• But, in this case as well, when interpolating a discrete substrate, Gaussian distributions can be replaced by many other (and probably far more effective) "smoothing functions". There are plenty of them. As in: Polynomial Interpolators for High-Quality Resampling of Oversampled Audio

• So far, the effects Gaussian broadening has been considered in coordinate space. Another way of looking at it is in the frequency domain, or 'momentum space'. This has already been done in Fuzzyfied Lissajous Analysis. But by far the simplest way is to study a single Fuzzyfied Sine function. It turns out that higher frequencies are damped with a factor   exp( - 1/2 σ² ω² ) .

• As a result of this damping, here are the pictures of the original and a fuzzyfied   y = sin(1/x)   function, together with executable and source code.

• Gaussian damping does not always result in a "neater" function, as is the case with the fuzzyfied Riemann function, where the fuzzyfied version is exploding even faster than the original.

• If it becomes desirable, indeed, to replace the Gaussian distribution by a far more general "function of small width and great height" in the future, then the following groundwork may become of value. It's in a 'sci.math' subtread of a thread called 'Disappointed' : 1, 2, 3, 4, 5, 6, 7, 8.

• Preliminary examples of such alternative shape functions are the rectangle, the triangle and the piecewise parabolic shape.

• A somewhat more recent development is the theory of Renormalized Equality. A theory which is perhaps more convincing because it is accompanied by technology: an application namely to Find the Differences in two nearly equal pictures (a children's puzzle).
  But the theory of Fuzzyfied Logic, which is contained in the same documentation & software bundle, is even more appropriate for this application.
  Here is a visualization of the fuzzyfied equality, as a function of x and y, according to the latter theory.

The Top Down Approach

As opposed to Discretization, how about Continuization ? What if not only top-down methods can be employed with the discrete, but even the discrete itself can be made continuous ? In fact, this is what actually happens with our Numerical Methods, as soon as discrete points are associated with so-called Shape Functions, in order to enable differentiation and integration. The latter being actions which are typically in the need of a continuous (and even analytical) domain. Finite element shape functions (or rather interpolations) are among the most elementary examples of functions which can be employed for the purpose of making a discrete substrate continuous (again). But there are others, like the bell shaped Gaussian curves, employed with Fuzzy Analysis. We have already decided to use the same name for these and for the shape functions in Numerical Analysis as well. I think what Applied needs is no more discretization, but continuization instead ;-)

An interesting pattern is emerging now. It is known that a continuous function can be discretized (sampled) by convoluting it with a comb of delta-functions. (Examples are in 'Discrete Linear System Summary' & 'Aliasing, Image Sampling and Reconstruction') But we have also seen the reverse now: a discrete function can be made continuous by convoluting it with a comb of shape functions. This is commonly called 'interpolation'. However, if Gaussian distribution functions are being employed as interpolants, then the discrete function values are actually a bit different from the continuized function values at the same place. Summarizing:

• Continuous Functions are Discretized by a comb of Delta functions
• Discrete Functions are Continuized by a comb of Shape functions

The Continuous and the Discrete are just two different means of looking at the same thing. Real matter isn't continuous or discrete. It's neither. It's both.

Our top down approach may also be called AfterMath :-). It's After the Mathematics. Post-processing instead of pre-processing.
But other name calling comes into mind as well. Smoothening can be considered as the modelling of a measurement process. The mathematical phenomenon is "sensed", so to speak, with a physical device, a sensor. Sensors always come with a spread σ , kind of a limited aperture, sort of fuzzyness, which makes any measurement vulnerable to a certain uncertainty. The common philosophy still is that these errors are not part of nature itself, but only part of our methods of observing it. But, according to Quantum Mechanics, "our" observations are part of the observed phenomenon itself ! Worse, it's not "us" who are observing nature. Nature is observing itself, with "us" as a medium, eventually. But not necessarily. It's no miracle that the electron observes it's own self energy (the name says it) by sending virtual photons back and forth to itself. It has a built-in sensor. Thus the sensor, the smoothening kernel, is part of the physical modelling, even in theory. It may be universal, so let's call it the Cosmic Sensor eventually. (Not to be confused with "Cosmic Censor" in the Cosmic Censorship hypothesis.)

The sources of the first document and (Delphi Pascal) test programs are included as well. Here are some results, for the 2-D and for the 3-D case respectively.
The core activity of renormalization is the calculation of a convolution integral with a shape function as a kernel. But, with the evaluation of these integrals, it makes a huge difference whether you integrate in one (dx), two (dx.dy) or three (dx.dy.dz) dimensions. So the dimensionality (1,2,3,4,..) is crucial with the successful continuization - yes or no - of singularities.

A typical example is the ideal gas law: p = c.T/V , where p = pressure, V = volume, c = constant, at a constant temperature T. No matter how you try, it's impossible to renormalize the function p(V) for V → 0 . This is due to the one-dimensional character of it. But, as everybody knows, nature has found a solution for the zero Volume problem: the ideal gas law is changed into something else, another law of nature. The gas becomes a fluid. And, under even more pressure, the fluid becomes a solid.

But, uhm .. on retrospect, it seems that my approach has been more difficult than necessary. A function   1/r   in 2-D may be simply renormalized as   1/√(r² + σ²)   and a function   1/r²   in 3-D may be simply renormalized as   1/(r² + σ²)   : a Cauchy distribution for the latter. The smaller σ is, the "better". Green lines in the pictures.
This argument is, however, misleading. Simplified renormalizations can only be substituted iff it has been firmly established that the original functions indeed get lost of their singularities with (the model of) some measurement. That is: the convolution with a shape function always comes first, simplification may come afterwards.

Three additional publications:

• Uniform Combs of Gaussians ( errata + source )
• Special Theory of Continuity ( errata + source )
• Cauchy distribution instead of Coulomb law?

These PDE's have been solved numerically. To that end, the same discretization method as with another ideal flow problem (Labrujère's Problem) has been employed. With help of the fluid tube continuum model, as a next step, the partial differential equations for the primary and secondary temperatures (heat balances) are set up:

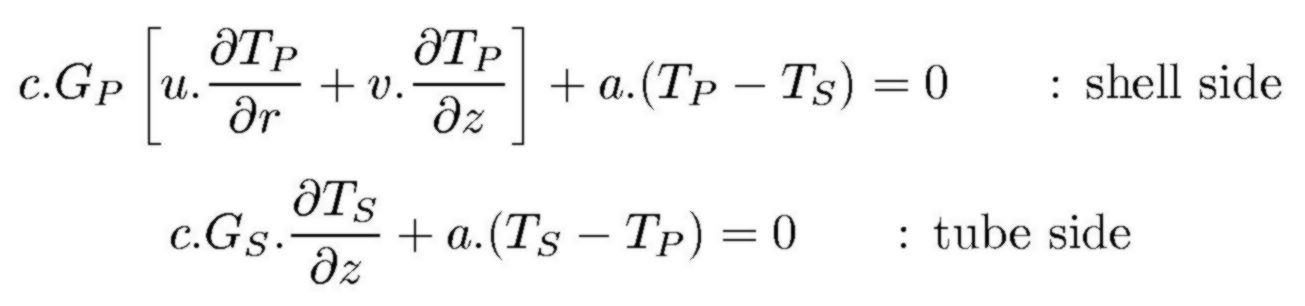
Having calculated the flow field, the PDE's for the temperature fields have to be solved too. To that end, several methods - none of them very revolutionary - have been employed. The resulting computer program, which calculates both the flow and the temperature fields and compares the latter with real experiments, is in the public domain. Further interesting details are found in a SUNA publication. Especially the statement that the assumption of Ideal Flow also gives rise to a higher safety margin with respect to the temperature stresses deserves attention. A neater representation of the proof hereof is disclosed too.

But the most interesting is that quite unexpected things may happen at the boundary between the Continuous and the Discrete! BTW, a Dutch version of the previous has been available for a couple of years ( > 1995); it's section 6.7 in my book. The Fluid Tube Continuum has as a tremendous advantage that the granularity of its discrete substrate is known: it is the pitch of the tube bundle. It is shown in the paper how this continuum breaks down for a certain critical primary mass flow, which so large, namely, that the heat can no longer be transferred within the distance of a pitch.

What relationship does there exist between a fluid tube continuum and the Prime Number Theorem ? Well, according to the prime number theorem, the (approximate) density of the prime numbers in the neighbourhood of a number x goes like 1/ln(x) . But, in order to be able to speak of a density, prime numbers must be subject to, yes: continuization. Like with the tube bundle of a heat exchanger, discrete items (tubes / primes) must be blurred, in such a way that things are not visible anymore as separate objects. In order to accomplish this, the same technology as with numerical differentiation might be employed:     P(x) = Σ_k f_k e^{-[(x - x_k) / σ_k]2 / 2}     with discrete values   f_k   at positions   x_k
Here the spread σ, too, has been made dependent on k . Now make all function values f_k equal to 1 . And next identify the positions x_k with the prime number positions. Then only the following question remains. What values must be designated to the spreads σ_k , in order to accomplish that the series P(x) represents a (n almost) continuous function ? Don't expect my contributions to Prime Number Theory to be of the same level as those to Numerical Analysis (?) But, nevertheless, I want to coin up my 5 cents worth, being the following conjecture:

        σ_k = √ x_k . ln( x_k )         (according to an estimate by von Koch)

Indeed, with these spreads, it turns out that the density distribution P(x) of the prime numbers is approximated very well by the theoretical result: 1/ ln(x) .
According to R.C. Vaughan (February 1990): It is evident that the primes are randomly distributed but, unfortunately, we don't know what 'random' means.
This is Experiment number 4 in the accompanying software, where the primes are replaced by random hits in a Monte Carlo experiment. And very well indeed, the abovementioned spread σ_k does not seem to be typical for prime numbers only !