Back to the Roots
Two main mechanisms are involved with a mathematical description of the world:
- Abstraction: giving rise to Science
- Idealization: giving rise to Mathematics
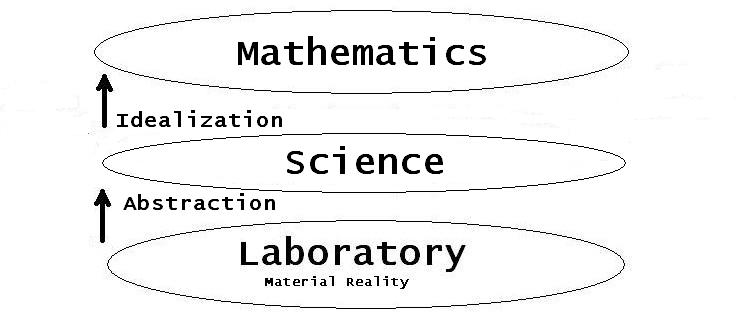
Abstraction
We shall argue that Abstraction
is not a mathematical but a physical activity. It's already
done by our senses. Our eyes can see the light, as it is casted back from a
piece of paper. The same piece of paper can be felt by our fingertips. And when
it is crumpled up, the sound of it will be heard by our ears. But eyes cannot
hear sound, fingertips cannot see light. All these single perceptions of our
senses have to work together. And even if we are not handicapped, the
end-result is still an abstraction of reality as a whole. None of our senses
is capable, for example, to see ultraviolet colors, as some insects can.
But why should attention be restricted to the creations of Nature? Why not
take a look at our own creations: human made Technology? Some cameras
are capable to "see" in the infrared domain. Our radio telescopes are even
capable to "see" the radiofrequencies of far away galaxies. Far more common
and well-known everyday abstractions of reality are performed, however, with
measuring devices like rods for the abstraction of lengths, clocks for the
abstraction of time intervals. But these measuring devices have become more
and more self supporting these days. When coupled with digital computers, human
interaction is hardly needed anymore. An example is the well known device for
the abstraction of weights: the balance. It's further development has resulted
in the fully automated
Mettler Balance, which is only one of the many examples though. All the
apparatus make an abstraction of reality, which is thus a physical and
not a mental process, let it only be that it would be mathematical.
From the Mettler balance example, we see that abstraction results in numbers.
Let us not be bothered by the question whether these numbers are numbers in a
mathematical sense. Likewise it is assumed that the outcome of an abstraction
can be another rudumentary mathematical object, like for example a naive "set".
Or even a complex number - as far as the latter is concerned, suppose that our
measuring device returns an ordered pair or real numbers. And let us not forget
geometry. Many laboratory devices come with a screen for displaying graphs.
Among the more advanced possibilities offered by modern instruments is three
dimensional modelling of the data received. The possibilities only seem to be
limited by lack of imagination. It doen't seem very wise to exclude anything a
priori and it's better to decide not to do so either. In short, we consider
any "primitive mathematical notion" as a possible product of abstraction, which
is thus a product of physics, not of mathematics.
Before proceeding any further, something has to be explained about a nasty
habit of some, (if) not all, theoretical mathematicians.
I want to talk about their systematical disdain for that continuing
activity of physicists, called measuring. Let it be stated firmly that
those theorists, in general, don't understand quite much about
performing experiments in the real world. Especially, they are not very much
aware of the fact that there exists a highly fundamental phenomenon out
there, which is inevitably and intimately related to any physical observation
of the continuum, inasmuch as to any realistic abstraction from it: the quite
limited accuracy of any measuring equipment. Always resulting, not in
one, but in several, distinct numerical values. For one and the same
physical quantity, we find a whole range of rational numbers, instead of
just one real. It is common practice to replace that range by a mean value and
kind of a deviation from the mean, called the measurement error. But the
word "error" alone seems to sound already most frightening to some.
Yet the whole secret of the continuum is in the error accompanying the
rational numbers, when abstracted from reality.
But, errors with rational numbers are by no means the exclusive intellectual
property of physicists. Not anymore. Because, with the advent of digital
computers, mathematicians have become experimentalists too ! Almost every
mathematician has a personal laboratory at his disposal these days. And - not
surprisingly - with these digital working places, the same kind of erroneous
behaviour is experienced as within the laboratories of physicists.
Computers have turned Mathematics into a die hard empirical Science.
Meanwhile,
many mathematicians have learned to live with the limitations of the apparatus.
They have learned how to cope with roundoff errors, error propagation and the
conditioning of matrices. They have learned how to clip straight lines against
the finite size of a window. To name only a few of the hurdles that had to be
taken in the early days of digital computing. However, physical experiments
do not constitute a physical theory. And mathematics cannot be reduced to just
the MatLab. It is precisely here that
idealization comes into mind.
Idealization
Yes, Idealization could be characterized as the true mathematical activity.
What is an idealization? Our answer: Idealization is where infinity comes in.
Among the most classical examples of idealization, without doubt, is good old
Euclidian Geometry - and perhaps it's even better to consider geometry in its
original setting: classical Greek philosophy. Remember utterings like: a point
has no size, a line is infinitely thin, parallel lines intersect at infinity.
The whole concept of an irrational number wouldn't have emerged if Euclidian
geometry hadn't been there in the first place. Yes, geometry is a playground
par excellence for infinities.
Yet, strangely enough, among the most challenging idealizations are not found
in pure mathematics, but in theories of Physics.
Most famous are the idealizations called Gedanken Experimente (Thought experiments
which were carried out by Albert Einstein in order to
establish the basic foundations for his (Special) Theory of Relativity.
In "The Theory of Heat Radiation"
by Max Planck,
Wien's Displacement Law (chapter III) can only be derived
under the following conditions: if the black radiation contained in
a perfectly evacuated cavity with perfectly reflecting walls is compressed
or expanded adiabatically and infinitely slowly. Idealized Carnot engines are used in Thermodynamics
for defining that stunning but indispensable quantity, called Entropy. And the list goes on and on.
How about ideal, frictionless movement in mechanics? How about ideal pendulums, which can
only exist through a sine with (almost) zero amplitude. As soon as physicists
have devised their mathematical model,
then it can be said that idealization
has been accomplished a great deal. One should become alerted as soon as the
following phrases are being uttered: "perfect", "ideal", "zero", but especially
"infinitely", like in "infinitely slow" or "infinitely thin". It can safely be
concluded, indeed, that the following is true.
Idealizations are invariably associated with Infinities.
Since we have established too that mathematics begins with idealizations,
it might be clear - finally - that this discipline, most probably: cannot do
without them.
Materialization
Far-fetched as some of them might seem, there is one thing which distinguishes
idealizations in Physics from idealizations in Mathematics. It is given by the
requirement that there should always be a correspondence between the physical
theory and physical experiments. With other words: the process of idealization,
in physics, must also exist the other way around. We shall give a name to this
inverse process of idealization and call it: MATERIALIZATION.
A little bit of Physics would be NO Idleness in Mathematics.
Thus we see that Idealization, as has been conceived by Plato and others, is
not so much wrong, but merely incomplete. It's not enough to idealize
things and stay there, in the heaven of Mathematics. It should be possible to
invert the whole process, as well. There must be a bijection.
Idealization must always be accompanied with materialization.
Besides that Stairway to Heaven, there should always exist a Way back to Earth.
Mathematicians, too, must go back to earth: iff they find it worthwile to know
that what they think may be labeled as scientific knowledge.
But let's go back to the lowest level for a moment. We have
seen that mathematicians have their own laboratories these days, installed at
modern personal computers. These Math Labs, essentially, exhibit the same
sort of peculiarities as the laboratories in physics. And, in very much the
same way, the need for idealization is felt here too. The reason is that there
exist two basic limitations with any digital mathematical experiment:
- in the Discrete domain: the limited size of (the set of) whole numbers
- in the Continuous domain: the limited size / accuracy of real numbers
Equivalent with the following Math Lab experiences:
- the limited number of words in computer memory
- the limited number of bits in a computer word
The continuing need for more processing power is closely associated with these
lack-of-space experiences. For if you have more space, and more bits, then you
need more processing power. And vice versa. Actually, what any mathematician
needs is an Ideal Computer:
- an unlimited number of words in computer memory
- an unlimited number of bits in a computer word
And all this, of course, associated with unlimited processing power. Look how
"easy" it is to formulate the goals of idealization with nowadays technology in
mind ! Nevertheless, these goals have been around for quite a while. Ever since
the Ancient Greeks formulated their idealized, Euclidian version of Geometry,
to be precise !
Meanwhile, good old geometry certainly has found its culmination in nowadays
computer animation, employed extensively in movies and games. But let us not
be distracted by the achievements of Modern Times so quickly.
After some thought,
it becomes evident that the three idealizations -
unlimited # words, bits and processing power - cannot live without each other.
It may be concluded that the idealizations which are needed with pure
mathematics are involved a great deal with the infinite, in (computer)
space and time. It may also be concluded that people cannot idealize one thing
(integer numbers) without the other (floating point numbers).
Therefore the Science of Mathematics is condemned to idealize everything.
Or nothing at all and stay primitive forever.
With the above in mind, it's
easy to see how the reverse process of idealization, materialization
(not to be confused with nonsense like
this),
may be realized with pure mathematics. Simply replace the infinite memory (and
infinite processing power) of their ideal computers by the finite memory (and
finite power) of real machines. Sounds good, but, to be honest, it's
not as simple as that ! Bringing pure mathematics back to earth has
given rise to brand new areas of investigation, such as Numerical Analysis
and Computer Graphics.
From my own experience, I can confirm that being involved with subjects like
NA and CG
is a highly non-trivial occupation. The mere requirement that
materialization should be possible doesn't mean that actually
doing
it would be a nice and easy task, to be accomplished in five minutes.
But, materialization being difficult is not the same as: finding that the way
back to earth comes to a dead end altogether. If the practitioners of Pure
Mathematics are allowed to pick up
their ideas out of the blue sky, then it cannot and it will not be guaranteed
that materialization is possible indeed. This makes pure mathematics vulnerable
to the criticism that some of its ideas may not be useful, meaning that there
is no way, at all, to
turn them into a useful application. These ideas just end where they are. They
are doomed to remain ideas. There is no way back to the abstractions and, via
the abstractions, back to the real world.
There is no recipe for idealization. Thus what it means can only be shown
by giving good and bad examples of it. Among the good examples are: Euclidian
geometry, which can be materialized to Computer Graphics; Classical Calculus,
which can be materialized to Numerical Analysis. Bad examples will be singled
out in the future, but only after their badness has been causing much harm to
the whole of mathematics.
Among these bad examples of (irreversible) idealizations are the Transfinite
Cardinals and Ordinals. Also some constructs related to the classical concept
of continuity have to be considered as inappropriate idealizations, because
they are void of any counterpart in real world matters. Point Set Topology
comes into mind. Anyhow, it is concluded from the above that the whole realm
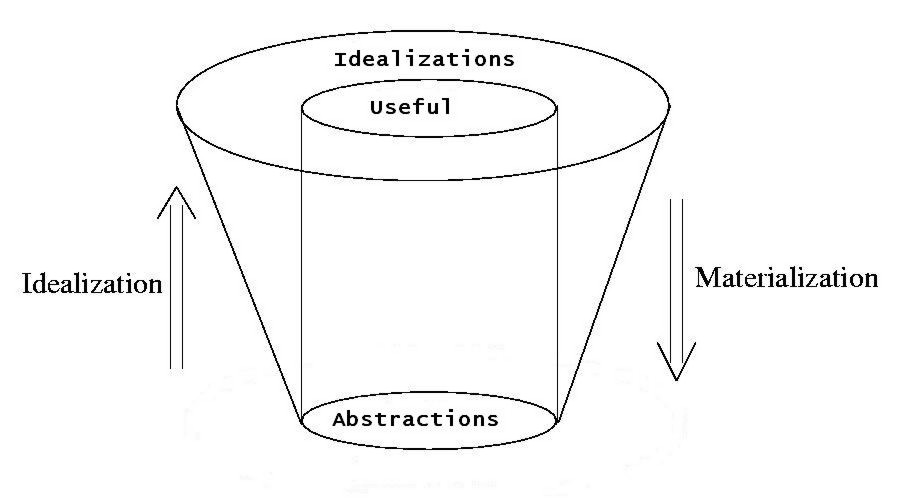
of Mathematical Idealizations can be splitted up in two distinct parts:
- Idealizations which can be materialized. They constitute the useful parts,
Snippets of Pure Applicable Mathematics.
- Idealizations which can not be materialized. Deemed to be useless,
it seems, for now and for all centuries to come.
How can it be decided, then, whether Idealizations can be transformed back into
Abstractions, which in turn have a counterpart in the Laboratory ? Well, let's
see then what makes Abstractions to Idealizations. It's the key activity of
Mathematics. It's the main motivation, the desire to be precise, the strive
for absolute perfection, absolute rigour, in short: to be exact.
Exactness means that all ambiguity has been removed, all errors have
disappeared. Exactness has a high price, however, as we have seen:
The one and only reason for Infinities to exist
is the act of Idealization.
There are NO Infinities in Abstract Science.
(See The Physics of Infinity)
Conclusion:
Infinities do only exist as Idealizations in the human mind.
There is only one way back to Earth. Away from the idealizations, back to the
abstractions. Away from the infinities, back to the finite. And that must be:
away from exact and re-introduce the errors. This is the subject of a
separate web page: Renormalization.
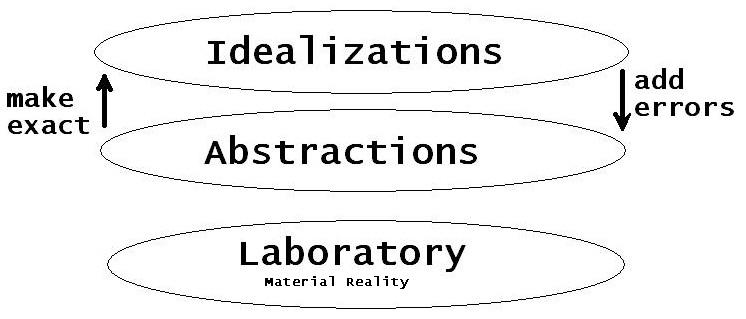
So we have a three-level system of the World that concerns us, Mathematics as
an activity in the real world (Math Lab), and as an activity of the Mind, and
everything in between:
- Laboratory. Or material reality. Here it is where our computers live in.
And program development. Number Crunching activity is all over the place. The
numbers here appear in two flavours: 32-bit integer and 64-bit floating point.
There are a few exceptions to this rule, but they are rare. Experimentation
also takes place here, like finding large prime numbers for the purpose of
encryption. But all kind of physical measurements as well.
- Abstractions. Here is the place where all Scientific Theories start.
Sometimes they stay here forever. There is also quite some mathematics here,
especially finitistic mathematics. Like Turing machines, computable functions,
a lot of Number Theory, Galois Fields. The whole machinery of Constructive
Mathematics (and maybe Intuitionism as well) is living here. Logic may be quite
different from the standard at this place: the law of excluded middle is
questionable. Numbers have a finite precision, but this precison can be much
larger than can be realized in any conceivable computer. And, oh yeah, all of
the infinitesimals, as employed for example by physicists. are to be
conceived as abstractions. They will only become idealizations - and only
eventually - in a later stage (e.g. when they become part of an integral).
- Idealizations. Cantorian mathematics is here in the first place. But also
Euclidian Geometry, Point Set Topology, the irrational numbers. Set Theory is
the governing principle here. In short:
it's the heaven of mainstream Mathematics. But the ideal pendulum is part of
the heaven's clock as well :-)
Do there exist mathematical theories that will never reach the stage of being
an idealization? There are! For example infinitesimals in e.g. Thermodynamic equations, like in e.g. T.dS = dU + P.dV , are "waiting"
for an integration procedure, before they become "mathematical".
Many mathematicians would argue that they are mathematical because
they are "meant" to integrated, but nobody knows what it means to say so.



