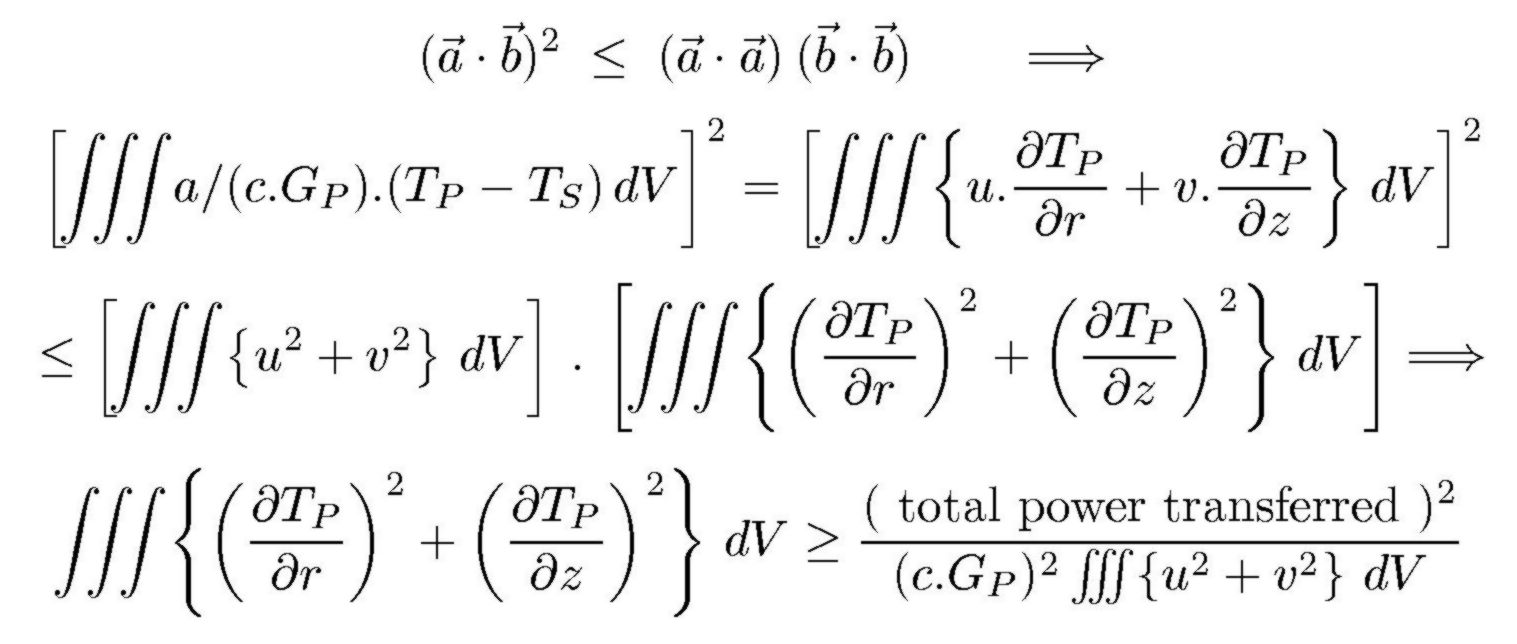With help of the Schwarz inequality, the square of term that represents the total heat transferred in the shell side equation can be written as follows:

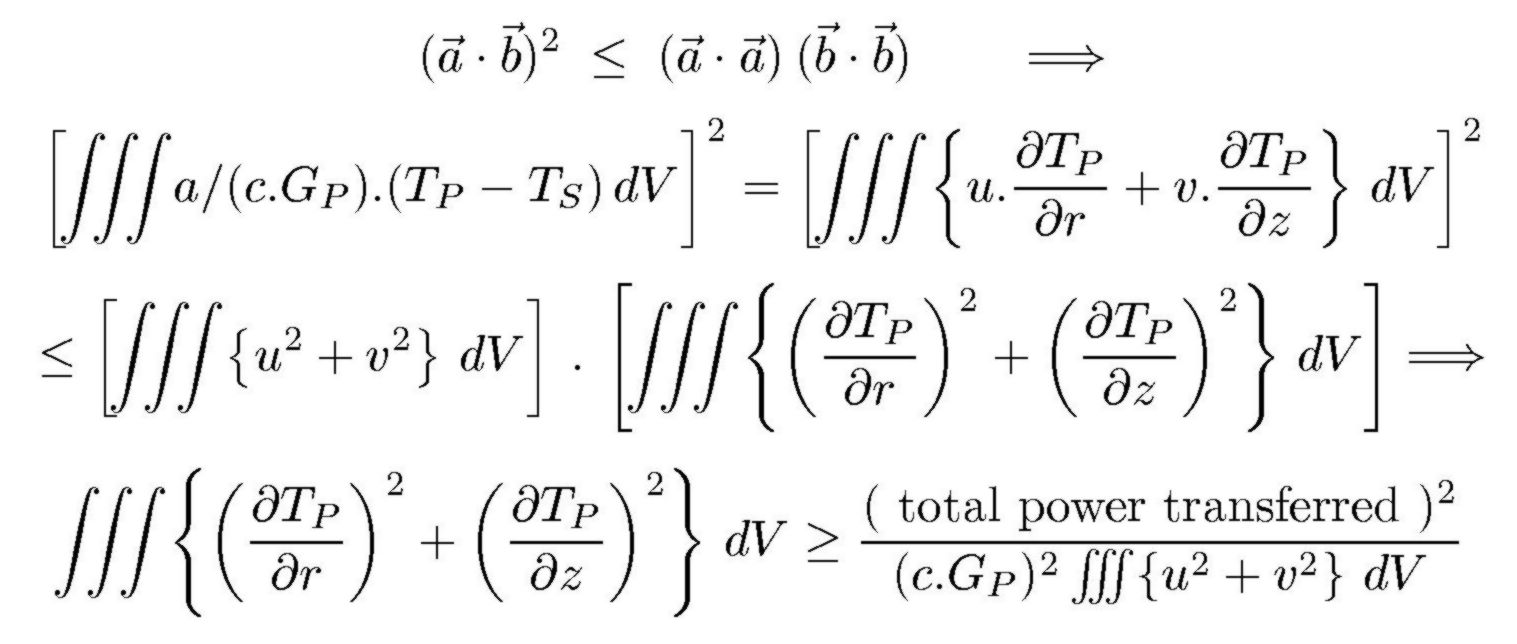
Here the denominator at the right hand side represents the kinetic energy of the flow field. It is known from theoretical fluid dynamics that this kinetic energy is minimal for ideal flow. The reason is this. Ideal flow is described by a potential function, which in turn is a solution of Laplace's equation. But Laplace's equation is equivalent with a minimization principle, where the absolute value of the gradient of the potential function is minimized. However, the gradient of the potential function is precisely the velocity vector. Thus the minimization principle denotes minimization of the kinetic energy of the fluid:
                ∫ ∫ ∫ [ u² + v² ] dV = minimal

It follows that the above left hand side is maximal for Ideal Flow fields. But this quantity is equal to the mean of the temperature gradients on the right and therefore equal to the mean temperature stress. Further details are published as a 'sci.math' article.