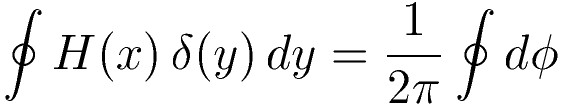
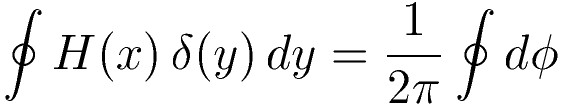
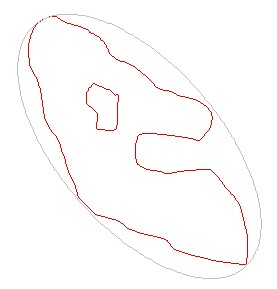
Here the boundary integral is taken around the area of interest. The coordinate
system is such that the inside / outside point is coincident with the origin,
which is simply a matter of convenience. Cartesian coordinates (x,y) are on the
left while polar coordinates (r,φ) are on the right.
The above is essentially an application of Green's Theorem. It is seen
that the left hand side is equal to:
∫∫ δ(x) δ(y) dx dy =
∫ δ(x) dx . ∫ δ(x) dy
The outcome of the latter integrals
depend on whether the point (0,0) is inside or outside the domain of interest.
In the former case they are unity (1), in the latter case they are zero (0).
Furthermore, I wouldn't know how to complete the proof of this theorem without
the key idea in
"Airy R.
Bean's Problem", where the delta function is seen as the limit, for
the variance / spread approaching zero, of a normal (Gaussian) distribution
function.
The right hand side is recognized as the winding number. Algorithmically speaking, using the
winding number is not as efficient, because angles are expensive to calculate.
Yet I have used a winding number algorithm for years, because it can be
implemented in a very robust way, such that "it never fails". Here comes
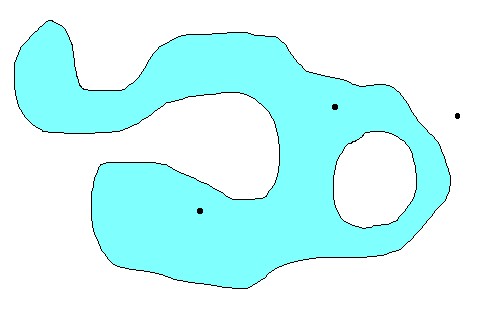
a (far too coarse grained) picture of the method:
 |
For the inside point (blue area) summing up the angles, while traversing the
boundary in counter-clockwise direction, results in 2π . Thus the outcome of
the winding number integral is 1 . For the outside point (white area) summing up the angles, while traversing the boundary in counter-clockwise direction, results in 0 . Thus the outcome of the winding number integral is 0 . |
H(x) = 0 for x < 0 and H(x) = 1 for x ≥ 0
δ is the Dirac delta function, which is may be defined as follows:
δ(x) = 0 for x ≠ 0 and δ(x) = ∞ for x = 0 in such a way that ∫ δ(x) dx = 1
Here is a visualization of the accompanying algorithm, which is also known as the crossing number method, as opposed to the winding number method:
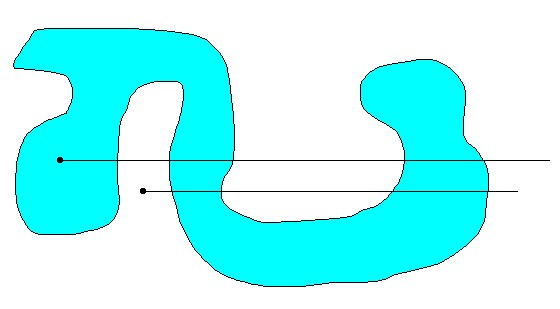 |
Draw a horizontal line from the point of interest to the right, towards
infinity (which is as far as necessary). A line to the left would have no sense,
because the Heaviside function H(x) is zero there, so there cannot be a
sensible contribution. This must be recognized as a clipping problem.
The delta function is integrated in vertical direction over all places where
our line to the right intersects the boundary. This results in a contribution
+1 where dy > 0 (upwards) or -1 where dy < 0 (downwards). Beware of the
special cases, though! See below. For the inside point (blue area) summing up all the +/- 1 contributions will result in 1 . For the outside point (white area) summing up all these contributions will result in 0 . |
You will find that a bit of Sorting and Searching is involved with an efficient implementation of the ray shooting method. It's quite advantageous, namely, to search for a delta strip of segments around the shooting ray. It's also very important to distinguish all special cases properly. Such as the positions of the contour segments (p,q) with respect to the ray:
q p p-q
> q | p |
= -----q--|--p--p-q--p---|--q-----
< | p | q
p-q p q
0 1 2 3 4 5 6 7 8
Last but not least, a lot of computational power shall be saved with the help
of proper preprocessing: see Bounding Ellipses below.
Han de Bruijn wrote: >> At least I hope that I've done _something_ new. Your hope is ill-founded. >> - can I find the "jewel of a formula" on this page somewhere else too ? The fact that the winding number equals the "crossing number" is well-known. Your awkward integral on the left may be new alas -- Robin Chapman, www.maths.ex.ac.uk/~rjc/rjc.html "Elegance is an algorithm" Iain M. Banks, _The Algebraist_Yet we can do surprising things with that "awkward integral". As is explained in the document, my "awkward" integral is a sharpening of a contour integral with an Error function (Erf) and a Gauss function in it. Which in turn is equivalent with a double integral over the domain of interest:
Nothing prevents us from keeping the spread σ finite. A consequence of
this is that the meaning of "inside/outside" becomes fuzzyfied; a point can be
"more or less" inside. Also take note of the fact that P(x,y) has become a
differentiable function now. And one could ask for the maximum value(s) of that
function. Which in turn is the same as asking for the so-called skeleton
of a figure. The latter problem has already been solved some time ago: see my
work on Contour Thinning. The gist
of our method is in the fact that there exists a relationship between the
gradient of P(x,y) and the running mean (μx,μy) :
P(x,y) [ μx - x ] = σ2 dP/dx
P(x,y) [ μy - x ] = σ2 dP/dy
Where 'd' denotes partial differentiation. "Running mean" because the vector
(μx,μy) is still a function of (x,y). Here is a
visualization of the iteration process:
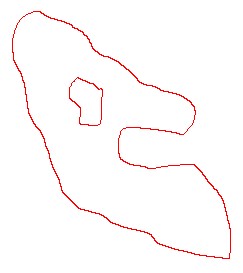 ==>
==>
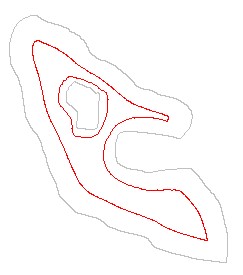 ==>
==>
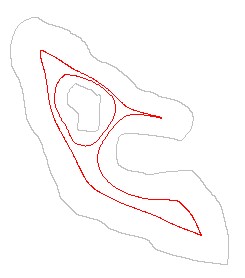 ==>
==>
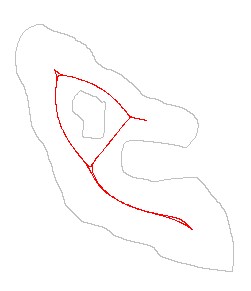
The iterations will eventually "come to rest" when x = μx and
y = μy .
∫ H[ cos(φ).(x-p) + sin(φ).(y-q) ] [- sin(φ).dx + cos(φ).dy ]
Here ∫ is a contour integral; H[] is the Heaviside step function;
φ is the angle of the normal of the straight line with the x-axis;
(p,q) is just a point on the line.
A picture says more ... :
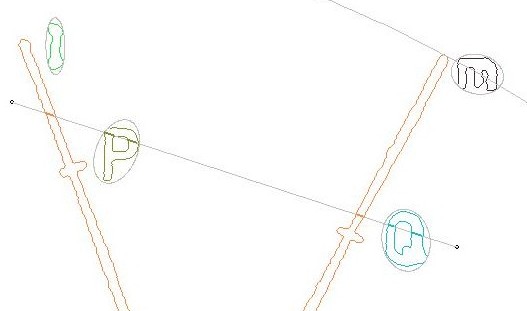
Bounding Ellipses
 |
When it comes to the preprocessing of domains and contours, Bounding Ellipses
are virtually indespensible. They are far more handsome that bounding boxes
of whatever kind. Quantities like midpoint and variances of a curve have to be
determined in the first place.
A bounding ellipse is then based upon the inverse tensor of inertia /
matrix of variances. The equation of an ellipse of inertia is given by:
σyy (x - μx)2 - 2 σxy (x - μx) (y - μy) + σxx (y - μy)2 = σxx σyy - σxy2 = D Where σ are the variances and μ are the midpoint coordinates. A bounding ellipse is defined as an ellipse of inertia which is slightly modified: the determinant D is replaced by a another constant E. σyy (x - μx)2 - 2 σxy (x - μx) (y - μy) + σxx (y - μy)2 = E Here E should be adapted in such a way that the whole boundary of the area of interest is contained inside the ellipse. Thus E is the maximum of: σyy (xk - μx)2 - 2 σxy (xk - μx) (yk - μy) + σxx (yk - μy)2 where (k) runs through all vertices of the boundary contours. |