index $ \def \SP {\quad ; \quad} \def \MET {\quad \mbox{with} \quad} \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} $
 Click on Pic (@ 1:00:00)
Click on Pic (@ 1:00:00)Critical reviews about the Hubble constant, theory versus measurements:

A more recent article was sent to me by Albert Welleweerd. It is titled A new measurement of the Hubble constant using Type Ia supernovae calibrated with surface brightness fluctuations. The value of the Hubble constant in there is $70,5$ (km/s)/Mparsec which is well in between $66.9$ (with help of the CMBR) and $74.0$ (with help of, say, the stars).
In case there exists more than one moment of creation - one for the universe as a whole ($A = -28.8$ billion years) and one for the earth in particular ($A = -4.9$ billion years) - then there is an issue that resembles the above discrepancies, if they still exist. The reason is the relationship between (intrinsic) Hubble time $\,1/H_i\,$ and Creation time $\,(T_0-A)\,$: $$ H_i(T_0-A) = 2 \slechts \frac{1}{H_i} = \frac{1}{2}(T_0-A) \slechts H_i = \frac{2}{T_0-A} $$ The Hubble time is determined from redshift data, resulting in an estimate for the (gravitational) age of the universe. This sort of knowledge is of course absent if we want to determine the age of the earth. But it's still possible to define a sort of Hubble constant for the Earth, by employing the above relationship: Hubble time is half Creation time, let it be so by definition. After all, Hubble constants are not really constants, so let's talk about Hubble parameters instead. $$ H_U = \frac{2}{T_0-A_U}\quad \mbox{with} \quad _U = \mbox{Universe} \SP H_E = \frac{2}{T_0-A_E}\quad \mbox{with} \quad _E = \mbox{Earth} $$ But if such is the case with the Earth, why not then with other objects / features in the universe, such as CMB, BAO, Cepheids, Red Giants, Quasars, Megamasers, Galaxies. They all may have different creation timestamps and hence different Hubble parameters.
From Earth Is Drifting Away From The Sun, And So Are All The Planets we quote: This year, 2019, our perihelion was 1.5 centimeters farther away than it was last year [ .. ] With every year that goes by, we find ourselves just slightly - 1.5 centimeters [ .. ] farther away from the Sun than the year before. [ .. ] the Earth, like all planets, is compelled to slowly drift away and spiral outwards from the Sun. Although the effect is small, this change of 1.5 centimeters per year is easily calculable [ .. ] And when we do those calculations, we find that the Earth migrates away from the Sun at ~1.5 centimeters per year. Easily calculable? Maybe yes. Question is: can 1.5 centimeters ever be easily observable? In comparison with 149597870700 meters? Whatever, even the most long ago epoch of creation cannot explain the Anomalous increase of the astronomical unit, as has been mentioned in Time Dilation, at least not quantitatively. According to Length Contraction and Hubble Parameter, assuming instruments with shrinking length $\,L\,$ to measure (therefore seemingly increasing) distances $\,r\,$ in empty space: $$ \frac{L_0}{L} = \frac{r}{r_0} = \frac{m}{m_0} = e^{H_i(t-t_0)} \hieruit \frac{r}{r_0}-1 \approx H_i(t-t_0) \approx \frac{\Delta r}{r_0} \hieruit \Delta r \approx H_i(t-t_0)r_0 $$ Then we calculate, with Hubble parameter $\,H_i\,$, astronomical unit $=AU=L_0\,$ and $\,t-t_0 =$ year:
> # 1 megaParsec
Mpc := 3.08567758*10^22;
# Hubble parameter (2022-02-08)
hubble := 73.4*1000/Mpc;
# Astronomical Unit (meter)
AU := 1.495978707*10^11;
# Year in seconds
year := 31556926;
# Drift away within 1 year
dAU := hubble*AU*year;
dAU := 11.22963443 # meter
It is clear that our outcome is three orders of magnitude (10 meters instead of 1.5 centimeters) out of range, if the above quotes in
red would be trustworthy. Clearly they are not, because
other
sources
come up with 15 centimeters for the Anomalous increase of the astronomical unit. Or, as quoted from Wikipedia's
Astronomical unit: The measurements of the secular
variations of the astronomical unit are not confirmed by other authors and are quite controversial.
> EM := 384.4*10^6;
dEM := hubble*EM*year;
dEM := 0.02885516655 # 2.89 centimeters
With an easier observation our easy calculation has led to a quite reasonable outcome: 2.89 cm and 3.78 cm are of the same order of magnitude.
Therefore it's not so much impossible that the expansion of empty space between the earth and the moon is at least part of an explanation.
From Wikipedia we quote: [ .. ]
the lunar orbit is gradually expanding. The rate of recession is $3.830 \pm 0.008$ cm per year. However, it is believed that this rate
has recently increased, as a rate of 3.8 cm/year would imply that the Moon is only 1.5 billion years old, whereas scientific consensus
supports an age of about 4 billion years. Another
Wikipedia page says:
The Moon is spiraling away from Earth at a rate of 3.8 cm/year. This rate has been described as anomalously high. And finally from
Why is Moon slowly drifting away from Earth: If the Moon continued to drift away from Earth at the same rate,
then it would have possibly collided with Earth around 1.5 billion years ago, which never happened in past.
Yes, there is a problem with that theory.
> earth := 4.54*10^9*year;
hubble := 2/earth;
dEM := hubble*EM*year;
dEM := 0.1693392070 # 16.93 centimeters
So let attention be restricted to cosmological ages instead.
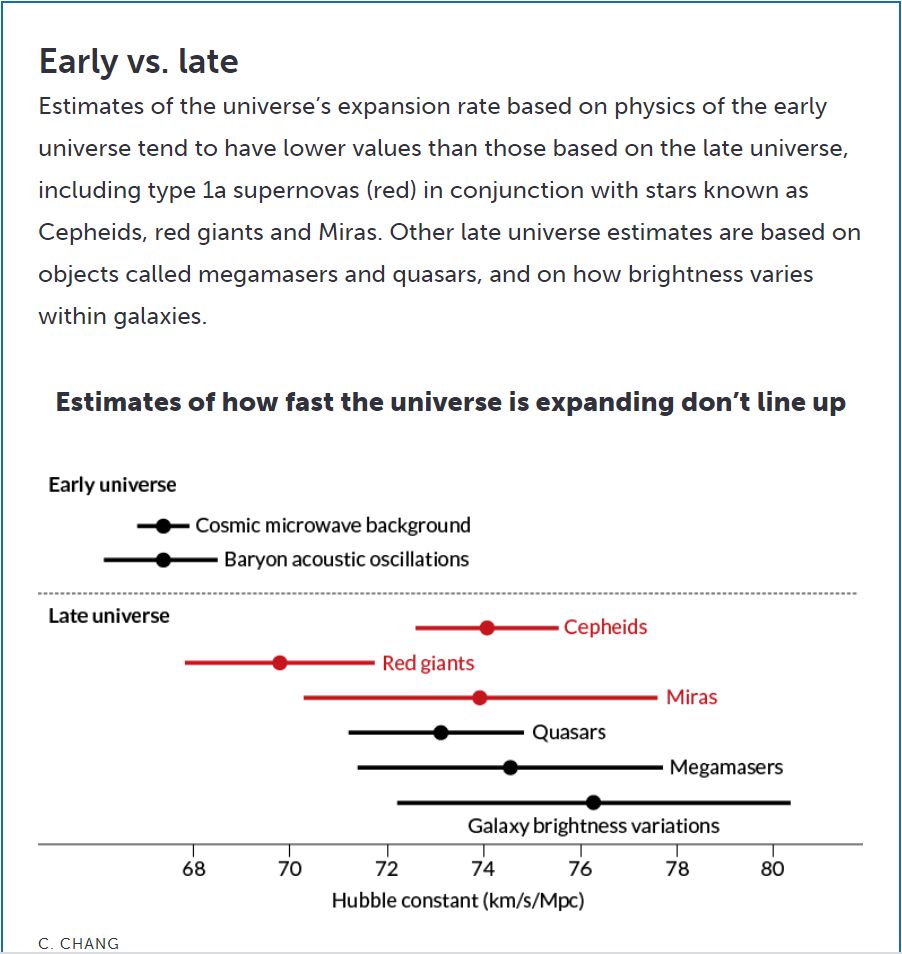
The Hubble tension: Is cosmology in crisis?
From that article the following values for the Hubble parameter are extracted. We find that the Hubble constant
has a value of about $73 \pm 1$ km/s per megaparsec. [ .. ] This value of the Hubble constant is called the "late time" version.
[ .. ] The sound waves of the Big Bang were locked into the early fireball, resulting in tiny variations in the CMB. [ .. ] Using this
"early time" information, astrophysicists predict that the Hubble constant should be about $67.5 \pm 0.5$ km/s per megaparsec.
Summarizing:
$$
H_{late} \approx 73\;(km/s)/Mpc \SP H_{early} \approx 67.5\;(km/s)/Mpc
$$
In the sections named Origin of Inertia and G. de Vauculeurs we have derived
the following formulas, with $G=$ gravitational constant and $\rho_0=$ mass density of the universe here and now.
$$
H^2 = \chi\,G\,\rho_0 \MET \chi = 8\pi \times
\begin{cases}
1/8 & (: \mbox{OI}) \\ 1/6 & (: \mbox{Mach}) \\ 1/3 & (: \Lambda\mbox{CDM}) \\ 0.3883945571 & (: \mbox{UAC})
\end{cases}
$$
Assuming that mass density is a constant, the (Mach) Hubble parameter divided by the (OI) Hubble parameter turns out to be approximately
equal to the "late" Hubble constant divided by the "early" Hubble constant. Thus serving as a possible explanation of the tension.
$$
\frac{H_{Mach}}{H_{OI}} = \sqrt{\frac{4}{3}} \approx 1.1547 \SP \frac{H_{late}}{H_{early}} \approx 1.0815
$$
An aproach that has been improved with help of this message by Richard Ravenhall (via A Cosmology Group):
'Hubble constant -- at 67.4 (+/- 0.5) km/sec/Mpc', NASA Science, July 22, 2018
'Hubble constant – at 73.2 (+/- 1.3) km/sec/Mpc', The Astrophysical Journal Letters, February 2021
Finally leading to the result (dated 2023 May 31): $$ H := \sqrt{\frac{0.3883945571}{(1/3)}} \times {\bf 67.4} = {\bf 72.7}5403614\,(\pm 0.5) = {\bf 73.2}\,(\pm 1.3) $$
The existence of two frames - Atomic versus Orbital, as has been accurately described in Support by Hoyle - turns out to be confusing (again). The clue may be that the gravitational constant $\,G\,$ is indeed constant in the Orbital frame but not in the Atomic frame. In the latter frame it varies like $\,G\sim m^{-2}\,$. Thus if we would have $\,G_1/G_2=m_2^2/m_1^2\;$ then it turns out to be alright. $$ \frac{H_1^2}{H_2^2} = \frac{\chi\,G_1\,\rho_1}{\chi\,G_2\,\rho_2} = \left(\frac{m_2}{m_1}\right)^2 \times \frac{m_1}{m_2} \\ \frac{H_1^2}{H_2^2} = \frac{\left[2/(T_1-A)\right]^2}{\left[2/(T_2-A)\right]^2} = \left(\frac{T_2-A}{T_1-A}\right)^2 = \frac{m_2}{m_1} $$ But I don't think we have it. So this might have become another Hubble tension. And a very serious one, it seems. I have been thinking that there is only one way out of the trouble and that is to boldly assume that $$ \left(\frac{T_2-A}{T_1-A}\right)^2 = \left(\frac{T_1-A}{T_2-A}\right)^2 \hieruit T_2-A = T_1-A $$ With other words: age in our theory would be independent of any (orbital) reference timestamp $\,T_0$ . Is age in UAC a constant then? Learning from A large numbers coincidence by Sahil Gupta we find that this stand is untenable:
It has become more and more convenient to adopt alternative notation, as presented in Time Dilated Past.
We repeat.
Let $H=$ Hubble parameter, $G=$ gravitational constant, $\rho_0=$ mass density here and now, OI = from Origin of Inertia, the book by Amitabha Ghosh, Mach = another value from the same book, VMT = version of the Variable Mass Theory (and ΛCMD = oh well). Then we have
$$
H = \sqrt{\chi G \rho_0} \quad \mbox{with} \quad \chi = 8\pi \times
\begin{cases}
1/8 & (: \mbox{OI}) \\
1/6 & (: \mbox{Mach}) \\
1/3 & (: \Lambda\mbox{CDM}) \\
0.3883945571 & (: \mbox{VMT})
\end{cases}
$$
But there are other theories saying that the Hubble parameter is in general inversely proportional to Age:
$$
H = \frac{n}{A} \quad \mbox{with} \quad
\begin{cases}
n=2 & (: \mbox{VMT}) \\
n=1 & (: \mbox{other})
\end{cases}
$$
According to the last set of formulas we have, like in the previous, but simpler:
$$
\frac{H_1}{H_2} = \frac{A_2}{A_1}
$$
The other way around is a bit more tricky.
$$
\frac{H_1}{H_2} = \frac{\sqrt{\chi G \rho_1}}{\sqrt{\chi G \rho_2}} = \frac{\sqrt{\rho_1}}{\sqrt{\rho_2}}
$$
The mass density $\rho$ is mass divided by expanding empty space. According to the section named
With other words
we have, for mass $M$, when integrated over a whole (part of the) universe
$$
M_1 = \rho_1 \int_0^R e^{-H/c.r}.4\pi r^2.dr \quad ; \quad M_2 = \rho_2 \int_0^R e^{-H/c.r}.4\pi r^2.dr
$$
The outcome is dependent on the point of observation $(1,2)$ in space and time.
Anyway, when talking about densities $(\rho_1,\rho_2)$ here and now, the above volume $[0,R]$ is far to large.
Sober thinking reveals that the calculations should be replaced by the following, over a very limited range $dr$
(ipse est infinitesimal when taken on a cosmological scale).
$$
m_1 = \rho_1 . 4\pi r_1^2.dr \quad ; \quad m_2 = \rho_2 . 4\pi r_2^2.dr \\
\rho_1 = \frac{m_1}{4\pi r_1^2.dr} \quad ; \quad \rho_2 = \frac{m_2}{4\pi r_2^2.dr}
$$
So now we have, with the expansion of empty space, that is with $r_1 \sim m_1$ and $r_2 \sim m_2$ :
$$
\frac{H_1}{H_2} = \frac{\sqrt{\rho_1}}{\sqrt{\rho_2}} = \sqrt{\frac{m_1/(m_1^2)}{m_2/(m_2^2)}} =
\sqrt{\frac{m_2 \sim A_2^2}{m_1 \sim A_1^2}} = \frac{A_2}{A_1}
$$
Great relief !! this is consistent with the above interpretation of the Hubble parameter as the inverse of an age.