Latest revision 27-01-2024

index $ \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} \def \SP {\quad ; \quad} \def \MET {\quad \mbox{with} \quad} \def \EN {\quad \mbox{and} \quad} \def \half {\frac{1}{2}} $

Origin of Inertia

Our key reference here is the book Origin of Inertia | Extended Mach's Principle and Cosmological Consequences by Amitabha Ghosh.
Jumping to Chapter 3: Mach's Principle and Inertial Induction. It starts with the (in)famous Bucket Argument by Newton himself. I have prematurely concluded in that section that Newton is right, Mach and Einstein (GR) are wrong. I'm sorry. One is never too old to learn. So let's scrutinize the Ansatz as proposed by Sciama, formula (3.2). The meaning of the symbols is as usual: $F=$ force, $G=$ Gravitational constant, $m=$ mass, $r=$ distance, $v=$ velocity, $c=$ speed of light (in empty space), $a=$ acceleration, $\rho=$ density, $H=$ Hubble parameter. $$ F = \frac{G\,m_1 m_2}{r^2} + \frac{G\,m_1 m_2}{c^2 r} a $$ This force has to be integrated accordingly, over a sphere with the radius of the universe. We have seen in Seeliger's Paradox that this "radius" is given by $\,1/\Gamma=c_0/H\,$. The Paradox is also the reason why only the second term is considered here. Numerical values from Amitabha's book (copied) give the final estimate. $$ F_a = \int_0^{c/H}\frac{G\,m(\rho\cdot 4\pi r^2\,dr)}{c^2 r} a = \frac{4\pi\,G\,\rho}{c^2}\half\left[\,r^2\,\right]_0^{c/H} ma = 2\,\frac{\pi\,G\,\rho}{H^2} ma \approx 1.8\; ma $$ This derivation would be not-done in UAC, because in our theory the universe has no "radius": it is infinite. There is a remedy, however. The density $\,\rho\,$ is subject to our Variable Mass Theory. Which means that, just like with resolving Seeliger's Paradox, we have instead: $$ F_a = \frac{4\pi\,G\,\rho_0}{c^2} \int_0^\infty e^{-\Gamma\,r} r\,dr\; ma $$ where: $$ \int_0^\infty e^{-\Gamma\,r} r\,dr = -\frac{1}{\Gamma}\left\{\left[e^{-\Gamma\,r} r\right]_0^\infty-\int_0^\infty e^{-\Gamma\,r}\,dr\right\} = - \left(\frac{1}{\Gamma}\right)^2 \left[ e^{-\Gamma\,r} \right]_0^\infty = \frac{c^2}{H^2} \\ \hieruit F_a = 4\,\frac{\pi\,G\,\rho_0}{H^2} ma \approx 2 \times 1.8\; ma $$ It's only a preliminary exercise, though, not the final word. Otherwise a finite universe would be in favour of an infinite one :-( Actually, as we shall see later on, the final word is more like this. $$ F_a = \frac{\pi\,G\,\rho_0}{H^2} ma = 1 \times ma $$ Where $\,m\,$ up to now has always been the gravitational mass. The goal of the book is to prove its most important result, namely the Origin of Inertia: inertial mass = gravitational mass, via Mach's Principle. We have decided to work the other way around and adopt the gravitational-inertial mass equivalence as an axiom, just like Albert Einstein did it. With that end-result in mind, we arrive at section 5.3: Law of Motion and Cosmic Drag. Only the force due to the acceleration is of interest to us, because UAC has quite another theory about the VDII (Velocity Dependent Inertial Induction). As quoted from page x in Origin of Inertia. In the Extended Mach's Principle such an interactive force acts on a body due to its velocity (in the mean rest frame of the universe) also. This force has been termed the Cosmic Drag. Such a velocity dependent term is clearly recognized in our own equation, as derived at the end of A Basic Equation section. Meanwhile we know that $\,\Gamma = c_0/H\,$. And $\,m_0\,$ is a test mass here and now. $$ e^{-\Gamma\,r}\;m_0\,\vec{a}_T = e^{-\Gamma\,r}\;\vec{F_T} = m_0\,\vec{a}_t\underbrace{-\half H\,m_0\vec{v}_t}_\text{Cosmic Drag Force} $$ Instead, however, we shall concentrate ourselves on the acceleration term of the force, as proposed in the book.


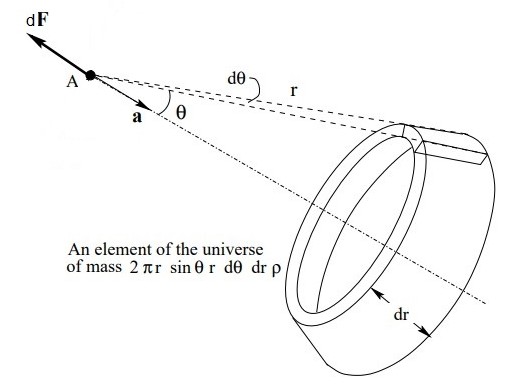
$$ dF_a = \frac{G\,2\pi r^2\,\sin(\theta)\,d\theta\,dr\,\rho\,m}{c^2\,r}a\,f(\theta)\cos(\theta) $$ An equivalent of formula (5.1), without the VDII, is $$ \vec{F}_a = - \vec{u}_a\frac{ma}{c^2}\int_0^\infty \chi\,G\,\rho\,r\,dr \MET \chi = 4\pi\int_0^{\pi/2}\sin(\theta)\cos(\theta)f(\theta)\,d\theta $$ If we skip all the way to (5.12) then it is motivated by the author that $\,\chi=\pi\,$, which furthermore is assumed throughout the book. We arrive at a slightly different result, though, by adopting the more simple assumption that $\,f(\theta)=\cos(\theta)\,$: $$ \chi = 4\pi\int_0^{\pi/2}\sin(\theta)\cos^2(\theta)\,d\theta = - 4\pi\int_0^{\pi/2}\cos^2(\theta)\,d(\cos(\theta)) = -4\pi\left[\frac{1}{3}\cos^3(\theta)\right]_0^{\pi/2} \hieruit \chi = \frac{4\pi}{3} $$ It is assumed, in UAC, that $\,G\,$ is indeed a constant. Thus the only thing that may be varying with distance is $\,\rho\,$. And the law governing that variation meanwhile is known. Only the acceleration term in (5.4) shall be calculated. The integral has been done before. $$ F_a = \frac{ma}{c^2}\int_0^\infty \chi\,G\,\rho\,r\,dr = \frac{\chi\,G\,\rho_0}{c^2}\,ma\,\int_0^\infty e^{-\Gamma\,r} r \,dr = \frac{\chi\,G\,\rho_0}{c^2}\,ma\,\frac{c^2}{H^2} = \frac{\chi\,G\,\rho_0}{H^2}\,ma $$ Now let us assume by axiom that, indeed, inertial mass = gravitational mass, then we have accordingly: $$ \frac{\chi\,G\,\rho_0}{H^2} = 1 \slechts H = \sqrt{\chi\,G\,\rho_0} $$ The result in Origin of Inertia is somewhat different from the (standard cosmology) formula (1.3) in the book by Fahr (2016). The meaning of the subscripts below is: $B=$ baryons (heavy elementary particles e.g. protons), $D=$ darkions (dark matter particles of unknown nature), $\nu=$ photons (the common particles of light), $\Lambda=$ vacuum "matter". $$ H^2 = \frac{8\pi\,G}{3}\left[\,\rho_B+\rho_D+\rho_\nu+\rho_\Lambda\,\right] \hieruit H = \sqrt{\chi\,G\,\rho_0} \MET \chi = \frac{8\pi}{3} $$ and $\,\rho_0 = \rho_B+\rho_D+\rho_\nu+\rho_\Lambda\,$. A more standard reference on the internet is of course Wikipedia: the Lambda-CDM model. We are talking about the first of the two Friedmann equations with the fuzz factors $\,k\,$ and $\,\Lambda\,$ set to zero and $\,a\,$ being the cosmic Scale factor: $$ \frac{\dot{a}^2 + kc^2}{a^2} = \frac{8 \pi G \rho + \Lambda c^2}{3} \MET \frac{\dot{a}}{a} = H \SP k=0 \SP \Lambda=0 $$ So we have at least three different values for the constant $\,\chi\,$. Let's give them a label as follows. $$ \begin{cases} \chi = \pi & (: \mbox{OI}) \\ \chi = 4\pi/3 & (:\mbox{Mach}) \\ \chi = 8\pi/3 & (: \Lambda\mbox{CDM}) \end{cases} $$ Or, as Louis Marmet says: Raw data have to be corrected for 'instrument and selection' biases before becoming "observations", and those corrections depend on the assumed cosmological model.
For people (like Louis) who think that a density $\,\rho_0\,$ of matter in the universe is not a meaningful concept, the formula may be used the other way around. Define an effective mass density by: $$ \rho_0 = \frac{H^2}{\chi\,G} $$ A Hubble parameter corresponding with the "Early universe" is used; see Hubble tension. Then we calculate (with MAPLE). 

G := 6.67408*10^(-11);
Mpc := 3.08567758*10^22;
H := 68*1000/Mpc;
OI := evalf(H^2/(Pi*G));
Mach := 3/4*OI;
LCDM := 3/8*OI;
                                            -25
                       OI := 0.2316196785 10
                                            -25
                     Mach := 0.1737147589 10
                                            -26
                     LCDM := 0.8685737944 10
Now compare the outcomes with a Google search on "density of the universe": The expansion rate we see today indicates that the critical density of the Universe is about $\bf \,9\times 10^{-27}\; kg \,m^{-3}\,$. This density, however, is the total density of both matter and energy. LCDM $=8.6\approx 9 \times 10^{-27}\; kg\,m^{-3}\,$. The bias by Google is clearly seen. As is confirmed by a weird statement in Wikipedia's Lambda-CDM model: A critical density $\,\rho_{crit}\,$ is the present-day density, which gives zero curvature $\,k\,$, assuming the cosmological constant $\,\Lambda\,$ is zero, regardless of its actual value. Substituting these conditions to the Friedmann equation gives the outcome.

$E=mc^2\;$ via Mach's Principle

Reading the book is resumed at 9.3 A Concept of Potential Energy in an Infinite Universe. Quote: If we consider the universe to be quasistatic, with the velocity and acceleration of all objects small, it may be possible to derive a concept of potential energy. When a particle is brought from infinity to a point at a distance $\,r\,$ from another particle, with the velocity and acceleration being infinitesimally small, it is possible to [ .. ] estimate the work done, as shown below. All of the mathematics is repeated here because there are too many typos (read: errors) in the orginal. And our approach, with UAC, is anyway different. With the usual meaning of the symbols, $E=$ as the potential energy, $m_0=$ test mass here and now, $M=$ mass somewhere in the universe, and Ei the so-called Exponential integral. In order to avoid confusion, minus signs are inserted on the left, not on the hand side. $$ - dE = \int_r^\infty \frac{G\,m_0\,dM}{x^2}\,dx = G\,m_0\,dM_0 \int_r^\infty \frac{\exp(-\Gamma x)}{x^2}\,dx \\ = G\,m_0\,dM_0\left[-\left.\frac{\exp(-\Gamma x)}{x}\right|_{x=r}^\infty - \Gamma \int_r^\infty \frac{\exp(-\Gamma x)}{x}\,dx\right] \\ = G\,m_0\,dM_0 \left[\frac{\exp(-\Gamma r)}{r} - \Gamma\operatorname{Ei}(\Gamma r)\right] \MET \operatorname{Ei}(x) = \int_x^\infty \frac{\exp(-t)}{t}\,dt $$ Using the above formulation, the potential energy of a particle with mass $\,m_0\,$ due to the matter of the universe contained in a spherical shell of radius $\,r\,$ and thickness $\,dr\,$, with the particle at its centre, is with $\,dM_0 = \rho_0\,4\pi r^2\,dr\,$ and $\,\xi=\Gamma r\,$: $$ - dE = G\,m_0 \left[\frac{\exp(-\Gamma r)}{r} - \Gamma\operatorname{Ei}(\Gamma r)\right]\rho_0\,4\pi r^2\,dr \\ - E = 4\pi\,G\,m_0\,\rho_0 \int_0^\infty \left[\,r\exp(-\Gamma r) - \Gamma r^2\operatorname{Ei}(\Gamma r)\,\right]\,dr \\ = \frac{4\pi\,G\,m_0\,\rho_0}{\Gamma^2}\left[ \int_0^\infty \xi\exp(-\xi)\,d\xi - \int_0^\infty \xi^2\operatorname{Ei}(\xi)\,d\xi\right] $$ Two integrals. At Mathematics Stack Exchange, Integral of exponential integral does not help much :-( $$ \int_0^\infty \xi\exp(-\xi)\,d\xi = - \left.\xi\exp(-\xi)\right|_0^\infty + \int_0^\infty \exp(-\xi)\,d\xi = 1 \\ \int_0^\infty \xi^2\operatorname{Ei}(\xi)\,d\xi = \int_0^\infty \operatorname{Ei}(\xi)\,d\left(\frac{1}{3}\xi^3\right) = \frac{1}{3}\left[ \underbrace{ \left.\operatorname{Ei}(\xi)\,\xi^3\right|_{\xi=0}^\infty }_0 + \int_0^\infty \xi^3\cdot\frac{\exp(-\xi)}{\xi}\,d\xi\right] $$ The first term is zero because of the Cauchy-Schwarz inequality: $$ \left[\int_\xi^\infty \frac{\exp(-t)}{t}\,dt\right]^2 \le \int_\xi^\infty \exp(-t)^2\,dt \;\cdot \int_\xi^\infty \frac{dt}{t^2} = \frac{1}{2} \exp(-2\xi) \cdot \frac{1}{3\,\xi^3} \hieruit \\ 0 \le \operatorname{Ei}(\xi) \le \frac{\exp(-\xi)}{\sqrt{6\,\xi^3}} \hieruit \\ 0 \le \operatorname{Ei}(\xi)\,\xi^3 \le \frac{\sqrt{\xi^3/6}}{\exp(\xi)} = \frac{1/\sqrt{6}}{1/\sqrt{\xi^3}+1/\sqrt{\xi}+\sqrt{\xi}/2+\sqrt{\xi^3}/6+\cdots} $$ And the last term is $$ \int_0^\infty \xi^2\exp(-\xi)\,d\xi = 2 \int_0^\infty \xi\exp(-\xi)\,d\xi = 2 \int_0^\infty \exp(-\xi)\,d\xi = 2 $$ Again we have in total (together with a result from C-decay Theories): $$ - E = \frac{4\pi\,G\,m_0\,\rho_0}{\Gamma^2}\left[ 1 - \frac{2}{3} \right] = \frac{4\pi}{3} \frac{G\,m_0\,\rho_0\,c_0^2}{H^2} = \frac{4\pi}{3} \frac{G\,m_0\,\rho_0\,c_0^2}{\chi\,G\,\rho_0} \hieruit $$ $$ - E = \frac{4\pi/3}{\chi}\;m_0\,c_0^2 = \frac{4\pi/3}{\chi}\;m\,c^2\MET \begin{cases} \chi = \pi & (: \mbox{OI}) \\ \chi = 4\pi/3 & (:\mbox{Mach}) \\ \chi = 8\pi/3 & (: \Lambda\mbox{CDM}) \end{cases} $$ There is a statement in footnote $\tiny 11$ at page 134 of the book: It is still more interesting to note that if we take the inclination effect $\,f(\theta)=\cos(\theta)\,$,   $\chi = 4/3\,\pi\,$ and the potential energy of a particle with mass $\,m\,$ is exactly equal to $\,- m c^2\,$, which implies that the total energy content of the universe is nil.

Pioneer anomaly

The last result in Seeliger's Paradox is repeated for convenience. $$ F = 2\pi\,G\,m\,\rho_0 \left\{ - \frac{1}{2\Gamma} + \frac{1}{2\Gamma} \right\} = 0 \MET \Gamma = \frac{H}{c_0} $$ $G=$ Gravitational constant, $m=$ mass of test particle, $\rho_0=$ density (mass/volume) of the universe here and now, $H=$ (intrinsic) Hubble parameter, $c_0=$ speed of light in empty space.
Some people think that a density $\,\rho_0\,$ of matter in the universe is not a meaningful concept. One reason is that exist huge irregular (fractal) structures out there. How to define an "infinitesimal" volume then in a sensible way? Let's have another quote from The Case for a Hierarchical Cosmology by Gérard de Vaucouleurs. I have discussed on several occasions since 1953 the growing evidence for a Local Supercluster (23-25), encompassing the majority of the nearby galaxies and groups with a center approximately in or near the Virgo cluster. The influence of this supercluster on galaxy counts can be detected at least down to m = 16 in the northern galactic hemisphere (26). Our Galaxy is in an outlying location, in our Local Group, near the southern edge of the system. Such an extreme case would possibly be covered by the following thought experiment.

Suppose that all matter is at one side of the test particle and calculate the force. $$ F = m\,a = m\,\frac{\pi\,G\,\rho_0\,c_0}{H} = m\,\frac{\pi}{\chi}\frac{H^2\,c_0}{H} $$ $$ \hieruit a = \frac{\pi}{\chi} c_0\,H \MET \frac{\pi}{\chi} = \begin{cases} 1 & (: \mbox{OI}) \\ 3/4 & (:\mbox{Mach}) \\ 3/8 & (: \Lambda\mbox{CDM}) \end{cases} $$ That sounds familiar. The Pioneer anomaly is an extremely small acceleration towards the Sun, of $\,(8.74 \pm 1.33)\times 10^{-10}\;m/s^2\,$. The Pioneer anomaly is also close to the free parameter $\,a_0\,$ in Mordehai Milgrom's MOND theory, where $\,a_0 \approx GM/R^2\,$ with $M=$ mass of a galaxy and $R=$ its radius. Previously proposed explanations include:The magnitude of the Pioneer effect $\,a_P = (8.74\pm 1.33)\times 10^{-10}\;m\,s^{-2}\,$ is numerically quite close to the product $=(6.59\pm 0.075)\times 10^{-10}\;m\,s^{-2}\,$ of the speed of light [ .. ] and the Hubble constant [ .. ] ipse est $\bf \,a_P = c_0\,H\,$.
It is clear that the value $\,\chi=\pi\,$ as employed in the book by Ghosh is to be preferred. Wikipedia proceeds with: hinting at a cosmological connection, but this is now believed to be of no particular significance. Of no particular significance? There is another clue: the acceleration is related to galaxies, via $\,a_P \approx GM/R^2\,$.

But maybe we are off with a factor two with our crude model: shouldn't the mass density be twice that amount if everything is at one side of the test particle? $$ F = m\,a_P = m\,\frac{\pi\,G(2\rho_0)c_0}{H} = m\,\frac{\pi}{\chi}\frac{H^2\,c_0}{H} $$ $$ \hieruit a_P = \frac{\pi}{\chi} c_0\,H \MET \frac{\pi}{\chi} = \begin{cases} 2 & (: \mbox{OI}) \\ 3/2 & (:\mbox{Mach}) \\ 3/4 & (: \Lambda\mbox{CDM}) \end{cases} $$

$\bf a_P=\;$.874e-9$\bf \;(m\,s^{-2})$ $\pi/\chi=2$$\pi/\chi=3/2$$\pi/\chi=1$ $\pi/\chi=3/4$$\pi/\chi=3/8$
$H = 67.7\;(km/s)/Mpc$.1315493851e-8.9866203879e-9.6577469253e-9 .4933101940e-9.2466550970e-9
$H = 73.0\;(km/s)/Mpc$.1418479336e-8.1063859502e-8.7092396682e-9 .5319297513e-9.2659648756e-9

Calculation details: 

c_0 := 299792458;
Mpc := 3.08567758*10^22;
google := 67.7; # Early universe
H := google*1000/Mpc;
chi := 2; chi*H*c_0;
chi := 3/2; chi*H*c_0;
chi := 1; chi*H*c_0;
chi := 3/4; chi*H*c_0;
chi := 3/8; chi*H*c_0;
google := 73.0; # Late universe
H := google*1000/Mpc;
chi := 2; chi*H*c_0;
chi := 3/2; chi*H*c_0;
chi := 1; chi*H*c_0;
chi := 3/4; chi*H*c_0;
chi := 3/8; chi*H*c_0;