index $ \def \MET {\quad \mbox{with} \quad} \def \SP {\quad \mbox{;} \quad} \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} \def \EN {\quad \mbox{and} \quad} \def \OF {\quad \mbox{or} \quad} \def \half {\frac{1}{2}} $

With other words

That may be so, but the "observed" universe, so much celebrated by certain empiricists, has an obvious drawback: it changes every year with the advent of a new telescope. It is not possible to build a sensible, and predictive, theory upon such a wildly varying concept.

So let's make a fresh start with theory. And, to quote Lewis Black again, "Nobody gives a shit" about "observed" or not.

1. The universe, as something that contains everything, does not exist. Way of speaking: it's infinite.
2. There does not exist another geometry in nature than common Euclidean geometry: there is space, there is time, but NO space-time.
3. Consequently, the Static Euclidean Universe (SEU), as repeatedly advocated by Eric Lerner, shall be adopted.
4. General Relativity is abandoned altogether. Newtonian gravity is retained. And of course The Big Bang never happened.
5. As a first approximation, the mass density distribution in the Static Euclidean Universe is everywhere the same / uniform.

Black Hole Universe

Formulas for the Hubble parameter $H$ are found in the thread "Big Bang: Tweak it or throw it out? " Only the one for the ΛCDM model is of interest to us in the current context: $$ H = \sqrt{\frac{8}{3}.\pi.G.\rho} $$ Now let us repeat, for the ΛCDM model and thus with GR conventions. $$ R \gt \frac{2GM}{c^2} \quad \mbox{with} \quad M = \rho\frac{4}{3}\pi R^3 $$ Herewith we derive: $$ 1 \gt \frac{(8/3.\pi.G.\rho)R^3}{c^2R} \\ \left(\frac{H}{c}R\right)^2 \lt 1 \\ R \lt \frac{c}{H} $$ A Static Euclidean Universe (SEU) with uniform mass density can only exist if it is finite (e.g. a sphere with radius $c/H$).

• An infinite Static Euclidean Universe is incompatible with a uniform non-zero mass density.
• A Static Euclidean Universe (SEU) with uniform mass density can only exist if it is finite.

1. The universe, as something that contains everything, does not exist. Way of speaking: it's infinite.
2. There does not exist another geometry in nature than common Euclidean geometry: there is space, there is time, but NO space-time.
3. Consequently, the Static Euclidean Universe (SEU), as repeatedly advocated by Eric Lerner, shall be adopted.
4. General Relativity is abandoned altogether. Newtonian gravity is retained. And of course The Big Bang never happened.
5. As a first approximation, the mass density distribution in the Static Euclidean Universe is everywhere the same / uniform.
   Jayant Narlikar actually has proved that GR is redundant, and replaced it by the Variable Mass Theory. The Universe's Expansion May Just Be An Illusion.

@ExpEarth writes to @khuramonline : You're right that the black hole universe I am describing can only describe a portion of the whole universe. It's the part that we can see. I should point out that the black holes I am talking about do not have a singularity and so, in a way, are not classic black holes. I think they are more similar to gravastars.

Precisely!

Black Hole Universe

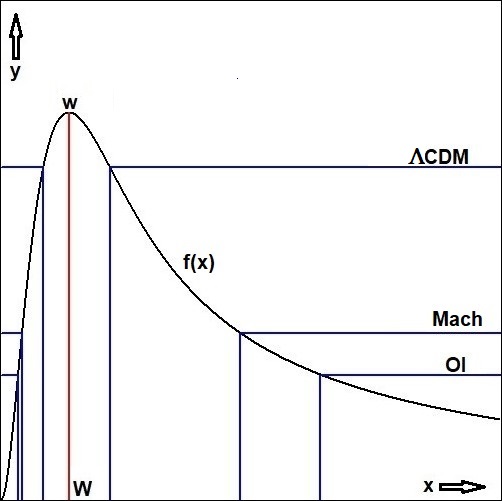
OI, Mach, ΛCDM denote different cosmological models, a limited set as studied by me. $$ H = \sqrt{\chi G \rho_0} \quad \mbox{with} \quad \chi = 8\pi \times \begin{cases} 1/8 & (: \mbox{OI}) \\ 1/6 & (: \mbox{Mach}) \\ 1/3 & (: \Lambda\mbox{CDM}) \end{cases} $$ The region for ΛCDM from which no light can escape or reach us (hence the Black Hole Universe) is calculated from $$ f(x) \gt \frac{1}{3} \quad \Longrightarrow \quad 2.096433787 \lt x \lt 5.451457921 $$ It's easy to calculate the maximum posible redshift for ΛCDM. $$ D = (c/H)\ln(1 + z) \quad \Longrightarrow \quad 1+z = e^{H/c.D} = e^x \quad \mbox{with} \quad f(x) = \frac{1}{3} $$ Solving for $x=2.096433787$ we find $z=\exp(x)-1=7.137099478$ as the maximally observable redshift with the ΛCDM model in our setting. However, according to @RedshiftDrift in Towards a Radical Change in Fundamental Physics, a value of $z = 13.2$ has been observed.

Contradiction with observation. This proves, with a ton of math, that the ΛCDM model cannot be alright.

G := 6.67408*10^(-11);
Mpc := 3.08567758*10^22;
c := 299792458;
H := 73.4*1000/Mpc;
w := 0.3883945571;
M_U := c^3/(w*G*H);
w := 1/8;
M_U := c^3/(w*G*H);

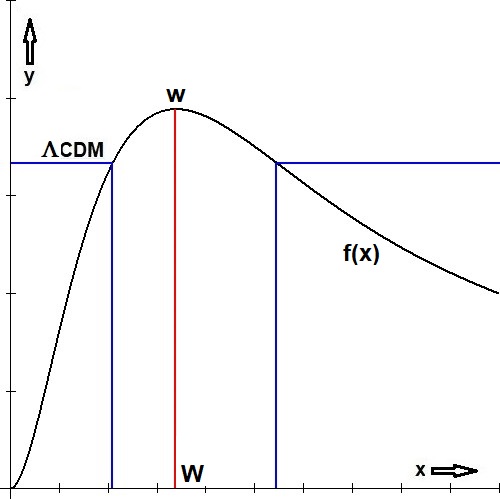
All values of the function must be below a certain value. For e.g. the ΛCDM model we have found that $f(x) \lt 1/3$ . For other values of $x$ that part of the universe is a Black Hole, meaning that no light from there can enter our cosmic bubble. We cannot observe anything where $f(x) \gt 1/3$, according to ΛCDM. However, alternative cosmic models can be devised. The most extreme one is defined by calculating the maximum of the function $f(x)$. Done numerically:

f(x) := (2-exp(-x)*(x^2+2*x+2))/x;
diff(f(x),x); s := fsolve(%=0,{x});
assign(s);
w := (2-exp(-x)*(x^2+2*x+2))/x;

                        s := {x = 3.383634283}

                          w := 0.3883945571

There are no epochs and eras in an Eternal Static Euclidean Universe. Therefore only the "last" one might be relevant.
For a dark-energy-dominated universe, the evolution of the scale factor [ .. ] is given in our own notation by $$ a(t) = a_0e^{H(t-t_0)} $$ with $H=H_0$ as a constant. By differentiation to $t$ it follows that $$ \frac{\dot{a}}{a} = H_0 \quad \mbox{and} \quad \frac{\ddot{a}}{a}= H_0^2 $$ The latter is indeed a speeding up of the expansion. This is all in concordance with the Variable Mass Theory. Because in Length Contraction it is argued that Length Contraction is observationally equivalent with the Expansion of Empty Space. So the latter is the reverse of the former. Formally: $$ \frac{L_0}{L(t)} = e^{H(t-t_0)} \quad \Longrightarrow \quad \frac{a(t)}{a_0} = e^{H(t-t_0)} $$ Which is exactly the same formula as with the dark-energy-dominated era in mainstream theory. The connection between mass density and the Hubble parameter is a bit different in our theory, but that's of minor importance now. $$ H_0 = \sqrt{w.8\pi G.\rho} \quad \mbox{with} \quad w = 0.3883945571 .... $$ Wikipedia's Accelerating expansion of the universe tells us another story with standard cosmology, though. First we assume, of course, that there is NO curvature of the universe, hence $\kappa=0$. Then we have the simplified formula $$ H^2 = \left(\frac{\dot{a}}{a}\right)^2 = \frac{8\pi G}{3}\rho $$ The so-called acceleration equation is aimed to describe the evolution of the scale factor with time: $$ \frac{\ddot{a}}{a} = - \frac{4\pi G}{3}\left(\rho + \frac{3P}{c^2}\right) \ne H_0^2 $$ Okay, I can be forgiving for the factor $4\pi/3$ and the term $3P/c^2$. But I don't comprehend the minus sign. How can there be an acceleration with a minus sign? I thought that must result in a slowing down instead of a speeding up.