Latest revision 11-11-2022
index
Time Dilation
$
\def \MET {\quad \mbox{with} \quad}
\def \EN {\quad \mbox{and} \quad}
\def \SP {\quad \mbox{;} \quad}
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \half {\frac{1}{2}}
$
There are many ways to measure time. A time measuring device is commonly called a
clock (Wikipedia).
Atomic clocks are involved with modern definitions of time. However, there seems to
be a problem with this. The following is a quote from the book
"Relativity Reexamined" by
Léon Brillouin.
We witnessed the invention of atomic clocks of incredible accuracy, whose physical
properties differ very much from the clocks Einstein imagined. This will be discussed
in some detail in Chapter 3. Let us mention here a real difficulty resulting from
internationally adopted definitions. The unit of length is based on the wavelength
of a spectral line of krypton-86 under carefully specified conditions with accuracy
$10^8$ and the unit of time is based on the frequency of a spectral line of cesium
with accuracy $10^{12}$. Hence, the same physical phenomenon, a spectral line, is used
for two different definitions: length and time, and the velocity $\,c\,$ of light remains
undefined and looks arbitrary. It should be stated, once and for all, whether a spectral
line should be used to define a frequency or a wavelength, but not both!
Indeed, according to
Wikipedia: "in 1967 the Thirteenth General Conference on Weights
and Measures defined the SI second of atomic time". Therefore, whatever is right
or wrong, time period $\,t\,$ (= 1/frequency) and wavelength $\,\lambda\,$ are nowadays
related to each other via the speed of light: $\,\lambda = c_0\,t\,$ . So the behavior of time
intervals $\,\Delta t\,$ can be derived easily. They are simply inversely proportional to
(sub)atomic mass $m$, just as it is the case with length, size and distances $\,\Delta L\,$.
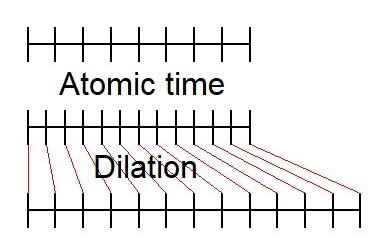
Length Contraction means atomic time Tick Contraction and hence
Atomic Time elongation. Because that's the way we trust our clocks! The time span may be
"the same" but we don't notice and find that it's longer:
Let $\,m_0\,$ be a reference elementary particle mass as it is here and now at a timestamp $(0)$
and let $\,m\,$ denote the same elementary particle mass mass after some change. Then we thus have:
$$
\frac{\Delta L}{\Delta L_0} = \frac{\Delta L/c_0}{\Delta L_0/c_0} = \frac{m_0}{m}
\hieruit \frac{\Delta t}{\Delta t_0} = \frac{m_0}{m}
$$
As a consequence of all this, according to Brillouin: the velocity $\,c_0\,$ of light [..]
looks arbitrary. Worse, the speed of light has been more or less defined nowadays
as being an absolute constant, thus leaving little or no room for such a thing as a varying
light speed eventually, as has been proposed by Setterfield
and others.
In my humble opinion, these matters are not as serious as they seem to be. It's just
how decisions are made between what's supposed to be constant and what's supposed to be varying.
It seems that we have some freedom in doing this. The worst that can happen is that certain
phenomena - hitherto regular - will show up in the future with some sort of anomalous behavior.
Whatever. So far so good about atomic clocks. The picture below is taken at 19:10 - 20:10 from
New Developments In Science, Part 3. Lightspeed and Atomic Behavior, which is
one of the You Tubes from Barry.
 Click on Pic
Click on Pic
Orbital time or gravitational time should be the time as derived from the earth's rotation around the sun, for example.
Assuming a Circular orbit
as a good approximation, we have according to good old classical mechanics for the orbital period $T$, say a year on earth:
$$
m \omega^2 r = G\frac{m M}{r^2} \hieruit \omega = \sqrt{G\frac{M}{r^3}} \hieruit
T = 2\pi\sqrt{\frac{r^3}{GM}}
$$
where $r=$ distance from earth to sun, $G=$ gravitational constant, $M=$ mass of the sun. Assuming
the varying elementary particle rest mass hypothesis for granted, we derive (more in general) for
the Orbital period
$\,T\,$ of any elliptical orbit ($\,a\,$ is the orbit's semi-major axis) that - indeed - it does not behave
like an atomic clock:
$$
T = 2\pi\sqrt{\frac{a^3}{GM}} \hieruit \frac{T}{T_0} = \sqrt{\frac{m_0}{m}} \ne \frac{m_0}{m}
$$
And so does not any subdivision of the year into months, weeks, days, hours, minutes, seconds:
$$
\large \boxed{\frac{\Delta T}{\Delta T_0} = \sqrt{\frac{m_0}{m}}}
\quad \not \sim \quad \large \boxed{\frac{\Delta t}{\Delta t_0} = \frac{m_0}{m}}
$$
The law even holds for an absurd one-dimensional case like this. Suppose we dig a tunnel through the whole earth, from the north pole
to the south pole. Then we go to the south pole
and drop a pinguin in it. How will it bounce? The Shell theorem
in Wikipedia helps us to set up the correct differential equation. A corollary is that inside a solid sphere
of constant density, the gravitational force within the object varies linearly with distance from the center [ .. ].
Let $R=$ radius of the earth and $r=$ that distance. Same end result is obtained all over the place.
$$
m\frac{d^2r}{dt^2} + G\frac{m M}{R^2}\frac{r}{R} = 0 \hieruit r(t) = R\cos\left(\frac{2\pi}{T}\,t\right)
\MET T = 2\pi\sqrt{\frac{R^3}{GM}}
$$
Just for fun, let's calculate the period of this
Journey through the center of the Earth.
It's 1 hour and 24.5 minutes:
# Gravitational constant
G := 6.6743*10^(-11);
# Mass of the earth
M := 5.9722*10^(24);
# Radius of the earth
R := 6378*10^3;
# Period of clock
T := evalf(2*Pi*sqrt(R^3/(G*M)))/60;
T := 84.48611832
From Wikipedia: The second (symbol: s)
is [ .. ] historically defined as 1/86400 of a day - this factor derived from the division
of the day first into 24 hours, then to 60 minutes and finally to 60 seconds each (24 × 60 × 60 = 86400).
However,
Earth's orbit around the Sun (a year) was much more stable than Earth's rotation. This led to proposals as early as 1950
to define the second as a fraction of a year. And then, at last, there was the advent of the
"Atomic" second.
Anyway an orbital second is different from an atomic second.
Let's revisit the equation $\,\omega = \sqrt{GM/r^3}\,$. Suppose that quantities are affected by Variable
Particle Mass. If we substitute back in Newton's equations, then we have, with primed (') the changed quantities and
otherwise the original ones here and now:
$$
\omega' = \sqrt{G\frac{M'}{r^3}} \slechts \omega\times\sqrt{m/m_0} = \sqrt{G\frac{M\times m/m_0}{r^3}}
\slechts \omega = \sqrt{G\frac{M}{r^3}}
$$
From this the following should become clear:
-
With Newton's laws alone - that is: with inertia and gravity and nothing else, in orbital time and empty space -
then it makes no difference whether (elementary) particle (rest) mass is varying or not.
Proof. Let $\vec{a}=$ acceleration, $\vec{r}=$ position, $T=$ orbital time, $G=$ gravity constant, $(M,m)=$ mass.
Employing a well known Finite difference
scheme for the second derivative (Second order central) we find:
$$
m\vec{a} \;\approx\; m\frac{\vec{r}(T+\Delta T)-2\vec{r}(T)+\vec{r}(T-\Delta T)}{(\Delta T)^2} = \frac{GMm}{r^3}\vec{r}
$$
It is known from Length Contraction that the position $\,\vec{r}\,$ is not affected by varying
particle mass because it is in empty space. This leaves us with the following variabilities (upon deleting $\,m\,$):
$$
\frac{1}{(\Delta T)^2} \sim M \slechts \frac{1}{\left(\sqrt{m_0/m}\right)^2} \equiv \frac{m}{m_0} \qquad \mbox{: unobservable}
$$
Thus it has no sense to mess up pure Newtonian calculations with varying elementary particle mass issues.
This holds true for planetary orbits, as an example. But take care! Even a mechanical device as simple as
a pendulum is not a pure Newtonian clock.
Length Contraction is applicable here and we have just found that acceleration varies with $\,m/m_0\,$:
$$
\mbox{Period of oscillation} = 2\pi\sqrt{\frac{L}{g}} \sim \sqrt{\frac{m_0/m}{m/m_0}} = \frac{m_0}{m}
$$
where $\,L\,$ is the length of the pendulum and $\,g\,$ is the local acceleration of gravity.
Conclusion: the ideal pendulum behaves like a (very primitive) atomic clock!
More important, however, is the following.
Orbital time and Atomic time can only be distinguished from each other
in combination - provided, of course, that Halton Arp's hypothesis is indeed true.
You can measure one with the other, but a variable time tick - orbital or atomic - cannot be measured with itself.
For the two pure clocks - orbital and atomic - this leaves us with only two possibilities:
- Atomic time is measured with Orbital time
- Orbital time is measured with Atomic time
It shall be assumed that the two clocks are always synchronized at timestamp $(0)$, i.e. $\Delta T_0 = \Delta t_0$
(and $T_0 = t_0$ eventually).
Orbital clock ticks are expressed in atomic clock ticks. Or atomic clock ticks are expressed in orbital clock ticks.
In either case we have infinitesimals in the limit:
$$
\lim_{\Delta\to 0}\frac{\Delta T/\Delta T_0}{\Delta t/\Delta t_0} = \frac{\sqrt{m_0/m}}{m_0/m} \hieruit \\
\frac{dT}{dt} = \sqrt{\frac{m}{m_0}} \slechts \frac{dt}{dT} = \sqrt{\frac{m_0}{m}}
$$
- The formula $\,dT/dt=\sqrt{m/m_0}\,$ shows how Orbital time $T$ is measured with Atomic time $t$
- The formula $\,dt/dT=\sqrt{m_0/m}\,$ shows how Atomic time $t$ is measured with Orbital time $T$
Furthermore it is clear that, with increasing elementary particle rest mass, $dt/dT = m_0/m < 1$. So atomic clock
ticks $dt$ shall become smaller than orbital clock ticks $dT$; atomic clocks are going to run faster than orbital
clocks. Consequently, in the future, time intervals measured with atomic clocks seem to be longer than time intervals
measured with orbital clocks. The reverse holds for the past, where orbital clocks have been running faster than
atomic clocks. But if orbital seconds have been shorter in the past and if time has been measured in these seconds too,
then perhaps things in the universe are not as old as they are assumed to be, with nowadays standard cosmology.
There is evidence. According to Wikipedia,
there exists an Anomalous increase of the astronomical unit: Recent measurements indicate that planetary
orbits are widening faster than if this were solely through the Sun losing mass by radiating energy.
Let's see. Because $m > m_0$ in the future we simply have:
$$
\frac{dT}{dt} = \sqrt{\frac{m}{m_0}} > 1
$$
Therefore planetary orbits - being gravitational clocks - should indeed be more increasing than expected,
that is: widening faster. The reverse might be true as well. Far aways (younger) objects in outer space
have lower elementary particle rest mass $m/m_0 < 1$ and therefore are expected to orbit faster.
A New Approach to Special Relativity is suggested in Léon Brillouin's book Relativity Reexamined, as we have seen already in
Length Contraction. The "new approach" starts with the mass-energy relation, and variable mass
is in there from the very beginning:
$$
E = mc^2 \EN m = \frac{m_0}{\sqrt{1-v^2/c^2}}
$$
So we have, according to the findings above, for atomic time:
$$
\frac{\Delta t}{\Delta t_0} = \frac{m_0}{m} = \sqrt{1-v^2/c^2}
$$
This means that clock ticks become smaller as velocity increases. Hence more clock ticks are needed in order to measure
the same time span as with "a particle at rest". Thus corresponding with Time Dilation according to Special Relativity.
Last but not least, let's talk about time according to Einstein, or Einstime for short.
The picture below is from Spacetime- Right or Wrong?
by Doug Marett (2013). The well known Time Dilation from Special Relativity is shown on the right.
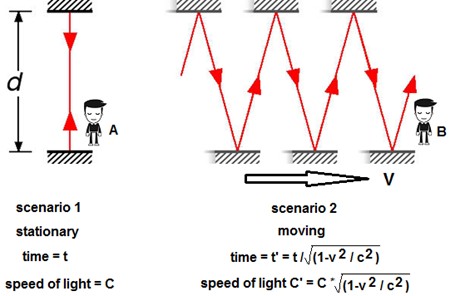
There exists a critical essay, written by Léon Brillouin
at the end of his life. The title of the booklet is Relativity Reexamined.
Quoting without permission from page 33:
Einstein's clocks were supposed to emit extremely short signals and to
accurately measure time intervals between signals emitted and received.
In a word, an Einstein clock was a radar system, and its requirements
were thus very different from those of a frequency standard.
With varying elementary particle mass according to UAC there is another time dilation in addition to the relativistic one.
It is already known that the arm length $\,d\,$ of the device (in the above picture) is shrinking,
so we have:
$$
\Delta t = \frac{2d}{c_0}=\frac{2d_0}{c_0}\frac{m_0}{m} \hieruit \frac{\Delta t}{\Delta t_0} = \frac{m_0}{m}
$$
Thus even the Light Clock as conceived by Albert Einstein (defining "Einstime") is no exception to the rule.
The arrow of time
Let's have a closer look / better listening at this video:
Sean Carroll on the Biggest Ideas in the Universe | Closer To Truth Chats
Right from the start, Sean Carroll says:
For example, the early universe has low entropy. That's where the arrow of time comes from.
At 40:30 minutes, Sean Carroll and companion start talking about time reversibility.
At 41:30 minutes:
[ Space and time ] are different, obviously, because, unlike space, time has a direction.
And I wrote a whole book on this [ .. ]:
From Eternity to Here.
The fact that entropy is increasing from the past to the future.
That statement is false, because in a universe with sustainable life forms order is increasing.
The above is typically a proposition that comes from a science whose only concern is dead matter.
It actually is a matter of life and death. Without enough life in existence, entropy is indeed increasing.
But increasing order due to the activity of living beings means: decreasing entropy of the universe.
And it's not where the arrow of time comes from.
The laws of physics seem to be in support of time reversibility.
But that is only the case if these laws can be considered apart from initial and boundary conditions.
Now let us only agree upon the fact that, in the end, all classical calculus boils down to Numerical Analysis,
for the simple reason that you must get numbers out. But Numerical Analysis is not continuous: it is discrete.
Within a discrete substrate, it's not at all obvious that the laws are independent of the boundary conditions:
The only natural thing about time is change. As for the rest,
Time Keeping is a complicated technical business - you need to keep up machines running to do it.
Time is man-made, so to speak, contrary to (one-dimensional) space: there is no such thing in physics as Length Keeping.
And there is more evidence, of a mathematical nature, that time is essentially different from length:
It's impossible to have a shortcut to the truth without the details. I'm sorry.


 Click on Pic
Click on Pic
