index $ \def \MET {\quad \mbox{with} \quad} \def \EN {\quad \mbox{and} \quad} \def \SP {\quad \mbox{;} \quad} \def \OF {\quad \mbox{or} \quad} \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} $
Now let UAC theory come in with its variable mass hypothesis and calculate again.
$$
R \gt \frac{2GM}{c_0^2} = \frac{2G}{c_0^2}\int_0^R\rho_0\,e^{-\Gamma r}4\pi r^2\,dr =
\frac{8\pi\,G\,\rho_0}{c_0^2}\int_0^R e^{-\Gamma r} r^2\,dr \hieruit \\ \frac{8\pi\,G\,\rho_0}{c_0^2\,\Gamma^3}
\left[-e^{-x}(x^2 + 2x + 2)\right]_{x=0}^{x=\Gamma R} \lt R
$$
This leads to a dimensionless expression and a pure mathematical problem. Namely what is $\,x=(\Gamma R)\,$ such that
$$
\frac{8\pi\,G\,\rho_0}{c_0^2\,\Gamma^2}
\left[ 2\,\frac{1 - e^{-x}}{x} - e^{-x}x - 2\,e^{-x} \right] \lt 1
$$
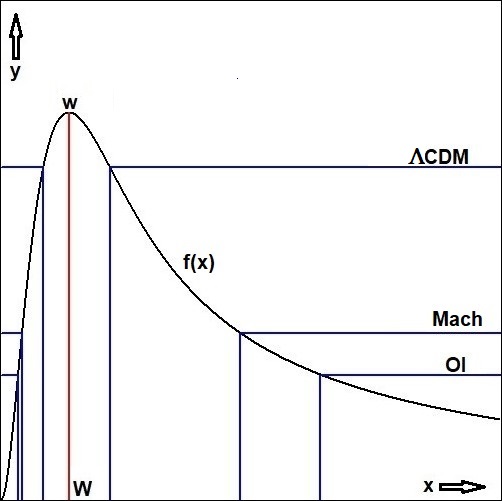
A few values of the function between square brackets (for $\,x\ge 0$) are given by
$$
f(x) = 2\,\frac{1 - e^{-x}}{x} - e^{-x}x - 2\,e^{-x} $$ $$
f(x) \ge 0 \SP f(0) = 0 \SP \lim_{x\to\infty} f(x) = 0
$$

Determine the maximum of the function and give names: $\,(W,w)\,$ with $\,f(W)=w\,$.
f(x) := 2*(1-exp(-x))/x-x*exp(-x)-2*exp(-x);
diff(f(x),x); s := fsolve(%=0,{x});
assign(s); # x = W
s := {x = 3.383634283}
w := 2*(1-exp(-x))/x-x*exp(-x)-2*exp(-x);
w := 0.3883945571
Hence the maximum value is given by $\,f(W=3.383634283)=w=0.3883945571\,$ and
$$
\frac{H}{c_0}R_O = W \hieruit R_O = 3.383634283 \times (\mbox{Hubble length})
$$
From Hubble volume in Wikipedia:
The Hubble length $\,c/H_0\,$ is 14.4 billion light years in the standard cosmological model, somewhat larger
than $\,c\,$ times times the age of the universe, 13.8 billion years. With our non-standard model we thus have
$$
R_O = 3.383634283 \times 14.4 \approx 48.7 \; \mbox{billion light years}
$$
Anyway the requirement for our universe not suffering from a big crunch is
$$
f(x) \lt \frac{H^2}{8\pi\,G\,\rho_0} \quad \mbox{where} \quad f(x) \le f(W)
$$
This would give the following extreme for the Hubble parameter
$$
\frac{H^2}{8\pi\,G\,\rho_0} = f(W) = w \hieruit H^2 = w.8\pi\,G\,\rho_0 \hieruit \large H = \sqrt{w.8\pi\,G\,\rho_0}
$$
We have found other possibilities in the Origin of Inertia section.
$$
H^2 = \chi\,G\,\rho_0 \MET
\begin{cases}
\chi = \pi & (: \mbox{OI}) \\ \chi = 4\pi/3 & (:\mbox{Mach}) \\ \chi = 8\pi/3 & (: \Lambda\mbox{CDM})
\end{cases}
$$
Respectively resulting in:
$$
\begin{cases}
f(x) \lt 1/8 \; : & x \lt 0.830482866 \OF x \gt 15.99973886 & (: \mbox{OI}) \\
f(x) \lt 1/6 \; : & x \lt 1.029356556 \OF x \gt 11.99369937 & (: \mbox{Mach}) \\
f(x) \lt 1/3 \; : & x \lt 2.096433787 \OF x \gt 5.451457921 & (: \Lambda\mbox{CDM})
\end{cases}
$$
with radius $\,R=x\cdot c_0/H\,$. Calculation details:
f(x) := 2*(1-exp(-x))/x-x*exp(-x)-2*exp(-x); fsolve(f(x)=1/4,x,0..4); # LATER fsolve(f(x)=1/4,x); # : see below fsolve(f(x)=1/3,x,0..4); fsolve(f(x)=1/3,x); fsolve(f(x)=1/6,x,0..4); fsolve(f(x)=1/6,x,4..100); fsolve(f(x)=1/3,x,0..4); fsolve(f(x)=1/3,x,4..100);It follows that all of the above possibilities are compatible with a homogeneous, isotropic, infinite, eternal, Euclidean universe.
Google up radius of Observable universe, then we find: The radius of the observable universe is therefore estimated to be about 46.5 billion light-years and its diameter about 28.5 gigaparsecs. So standard is not far off when compared to a non-standard $\,R_O \approx 48.7$ billion light years. Together with the speed of light and a Hubble parameter (both with Google) we calculate
R := 28.5/2*10^3; # Mpc
c := 299792.458; # km/s
H := 69.8; # (km/s)/Mpc
x := R*H/c;
x := 3.317795273
Thus resulting in a value which is well within any of the "forbidden" areas for that dimensionless radius and close to
$\,W = 3.383634283\,$. We think that an interpretation of the above must be that, in UAC theory, there also exists a radius $\,R_O\,$
of the observable universe, the inside of a "Black Hole" so to speak, beyond which no light can escape. However, our "Black Hole" is
assumed to be a Dark_star (Newtonian mechanics), meaning
that there is no gravitational collapse; otherwise our observable universe would not even exist. Now suppose that a bright star is
at a distance $\,R_O\,$ from us, then, with respect to that star, the earth is at a distance $\,R_O\,$. Consequently, the light from
that star cannot escape beyond that distance and thus it shall be invisible to us. So everything outside that "Black Hole" /
our "Cosmic Bubble" cannot be observed by us human beings. The magnitude of $\,R_O\,$ depends on the model employed, namely:
$$
R_O = \frac{c_0}{H} \times \begin{cases}
x = 0.830482866 & (: \mbox{OI}) \\ x = 1.029356556 & (: \mbox{Mach}) \\ x = 2.096433787 & (: \Lambda\mbox{CDM})
\end{cases}
$$
However, it is suggested that, independent of any model, a value of $\,x\,$ that cannot be surpassed is $\,x=W=3.383634283\,$.
It can also be argued that there are no "forbidden" Black-Hole-like regions in our universe.
A by-product of the above is the mass $\,M\,$ of the whole universe, whether observable or not.
$$
\frac{2GM}{c_0^2} = \frac{8\pi\,G\,\rho_0}{c_0^2\,\Gamma^3}\lim_{x\to\infty}f(x).x = 2\frac{8\pi\,G\,\rho_0}{c_0^2\,\Gamma^3}
\hieruit M = \frac{8\pi\,\rho_0}{\Gamma^3} = 6\,\rho_0\,\frac{4}{3}\pi \left(\frac{c_0}{H}\right)^3
$$
For the Observable part of the universe we calculate that approximately two third of the total mass is in there.
x := 3.383634283; fx := evalf(2*(1-exp(-x))-exp(-x)*x^2-2*exp(-x)*x);$$ M_O = 1.314185140 \times \frac{4\pi\,\rho_0}{\Gamma^3} \approx 4\,\rho_0\,\frac{4}{3}\pi \left(\frac{c_0}{H}\right)^3 $$ If we give credence to the Lambda-CDM model, then there also exists a critical density $\,\rho_{crit}\,$ which according to (the GR version of) our own theory must be slightly smaller than the ΛCDM value: $$ \rho_{crit} = \frac{H^2}{w\times 8\pi G} = 7.454393805\times 10^{-27}\;kg/m^3 $$ Calculation details:
G := 6.67408*10^(-11); Mpc := 3.08567758*10^22; H := 68*1000/Mpc; w := 0.3883945571; rho := evalf(H^2/(w*8*Pi*G));It has been suggested that, independent of any model, a value of $\,x=\Gamma r\,$ that cannot be surpassed is $\,x=W=3.383634283\,$. This idea allows us to make an estimate of the maximally possible (cosmological / non-Doppler) redshift $\,z_{max}\,$ in the universe which is observable by us. $$ \frac{\lambda}{\lambda_0} = \exp(W) \hieruit 1+z_{max} = \exp(3.383634283) \SP \boxed{\Large\;z_{max} \approx 28.5\;} $$ It means that Olbers' Paradox for our infinite universe is effectively solved: almost none of it is observable here and now. In comparison, the maximally observable redshift with ΛCDM values in a Static Euclidean Universe (SEU) is $\,\exp(2.096433787) = 8.137\,$, which actually has been surpassed already by the Hubble Space Telescope (HST) with its discovery of the high-redshift galaxy GN-z11. Up until the discovery of JADES-GS-z13-0 in 2022 by the James Webb Space Telescope, GN-z11 was the oldest and most distant known galaxy yet identified in the observable universe, having a spectroscopic redshift of z = 10.957, which corresponds to a proper distance of approximately 32 billion light-years (9.8 billion parsecs). Keep up the Guinness World Record of the most distant confirmed galaxy in Wikipedia's List of the most distant astronomical objects.
Reference is "Detection of the cosmological time dilation of high-redshift quasars". The same method as in that thread 96 can be employed to calculate the age $(T_0-T_O)$ of stars at the edge of our Observable universe. That age must be expressed, of course, in orbital time, because the age of the universe in atomic time is simply eternal. According to Narlikar's Law we have: $$ \left[1+\frac{1}{2}H(T-T_0)\right]^2 = \frac{m}{m_0} = e^{H(t-t_0)} \SP 1-\frac{1}{2}H(T_0-T_O) = \sqrt{e^{-H/c.R_O}} = \sqrt{e^{-W}} \\ (T_0-T_O) = 2\left(1-e^{-W/2}\right)\times\frac{1}{H} \hieruit \mbox{age} \approx 1.63 \times \mbox{(Hubble time)} $$