UAC index
$
\def \half {\frac{1}{2}}
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \OF {\quad \mbox{or} \quad}
$
What is the proper way to do DTFE
The density which is generated by the Cauchy distribution is repeated
here for convenience. It shall be modified slightly for our purpose. An educated guess is the Ansatz:
$$
P(x) = (N+1) \, \frac{d/\pi}{d^2+x^2} \sim \frac{1}{1+(x/d)^2}
$$
The interval of interest is $\left[-\infty,\infty\right]$. Resulting in:
$$
(N+1) \int_{-\infty}^{x_k} \frac{d/\pi}{d^2+t^2} \, dt =
\frac{N+1}{\pi} \int_{-\infty}^{x_k} \frac{d(t/d)}{1+(t/d)^2} =
\frac{N+1}{\pi} \left[\arctan(x_k/d)+\half\pi\right] = k+1
$$ $$
\hieruit \arctan(x_k/d) = \frac{k+1}{N+1}\pi - \frac{\pi}{2}
\hieruit x_k = d \tan\left( \left[ \frac{k+1}{N+1}-\half\right] \pi \right)
$$
Where the possible values of $\,k\,$ in the sequence $\,x_k\,$ should preferrably be
restricted to $\,0 \le k < N-1\,$. If $\,x_k\,$ is at the interval $\,[-1,1]\,$ then:
$$
1 = x_{N-1} = d \tan\left( \left[\half - \frac{1}{N+1}\right] \pi \right) \hieruit
d = 1/\tan\left( \left[\half - \frac{1}{N+1}\right] \pi \right) \\
-1 = x_{0} = d \tan\left( \left[\frac{1}{N+1} - \half\right] \pi \right) \hieruit
d = 1/\tan\left( \left[\half - \frac{1}{N+1}\right] \pi \right)
$$
Thanks to our educated guess, both results for $\,d\,$ are the same, as should be.
Below is a picture of the result, everything scaled properly at $\,[-1,+1]\times[0,1]\,$.
The exact function is colored black, the Voronoi histogram is colored green,
function behaviour at the 1-D Delaunay "triangles" is colored red.
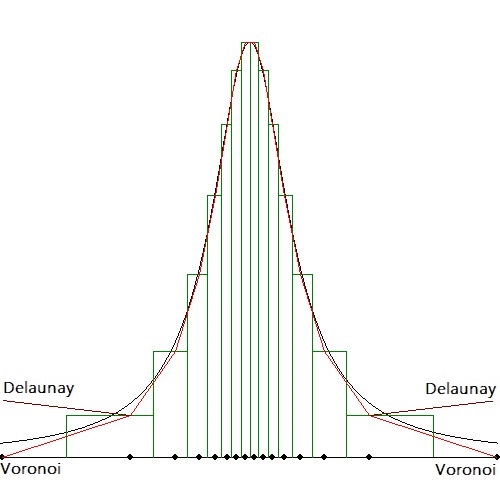
Especially mind the zero function values at the boundary points $\,(-1,0)\,$ and $\,(+1,0)\,$.
The latter happens because the size of the Voronoi regions belonging to the end points extend to infinity,
therefore the corresponding reciprocal values must be zero. But, on the contrary, if we take the 1-D equivalent of Delaunay triangles
everywhere, then the field estimator gives too high values (colored Maroon) at the boundary points.
Let's extend now the one-dimensional method as presented above to the two-dimensional case.
Actually, this has been done before; so, in some sense, I'm just re-inventing the wheel. The 2-D generalization is known as the
Delaunay tessellation field estimator.
It has been developed by two astronomers: Willem Schaap & Rien van de Weijgaert. There is an accompanying
thesis
Our own development, not surprisingly, has started with a study of Voronoi & Delaunay
tessellations, initially as a part of our Implementable Set Theory.
For the purpose of obtaining a Field Estimator of a two-dimensional discrete point set (called sites), for each point of the set
an area has to be defined. There are essentially two ways of doing this:
- The Field value at a site is the reciprocal of the area of the Voronoi region surrounding the site
- The Field value at a site is the reciprocal of the area of all Delaunay triangles surrounding the site
Where it is noticed that the Field values should be normed. A suitable way to do this is to determine the maximum value in the field
and divide all field values by it.
The Delaunay method (2) is much easier to implement than the Voronoi method (1). Both methods have been tried. For the one-dimensional case
it makes no difference, except at the boundary, where the field values are zero with the Voronoi method and non-zero with the Delaunay method.
Approximately the same seems to hold for the two-dimensional case, as discussed cleverly in this Question at the Mathematics Stack Exchange forum:
When is 2d sparse numerical integration by Voronoi regions better than using triangular mesh elements. Quoted from one of the answers:
Schaap gives cogent reasons as to why the Delaunay weighting (DTFE) is to be preferred over Voronoi weighting (VTFE). I disagree;
it's more correct to assign (the area of) a Voronoi region to a site, simply because of the mathematical neighborhood Definition:
Given points $P = \{p_1,\cdots,p_n\}$ the Voronoi region of point $p_i$, $V(p_i)$ is the set of points at least as close to $p_i$
as to any other point in $P$:
$$
V(p_i) = \left\{x \left|\;|p_i-x| \le |p_j-x| \right. \;\forall \, 1 \le j \le n \right\}
$$
Another advantage is that the field values at the boundary sites must become zero, because the Voronoi regions extend to infinity there
and the reciprocal value of an infinite area is zero. Take a good look at some
pictures in the Wikipedia article. I've always thought that a Delaunay tesselation is always delimited by a convex hull as
the proper boundary. Nothing of the kind is observed here.
But allright, let us take a look at our end-results for a test mesh of triangles in a cicular arrangement:
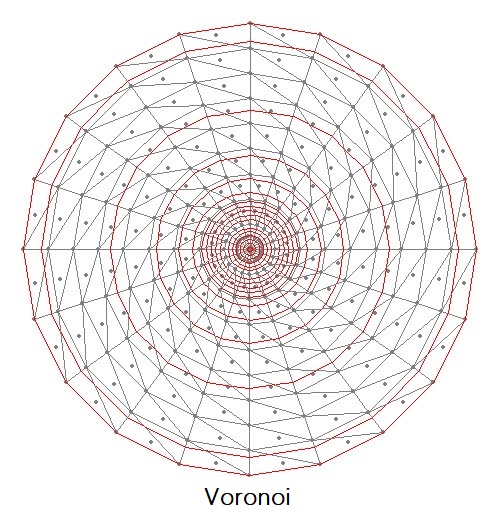
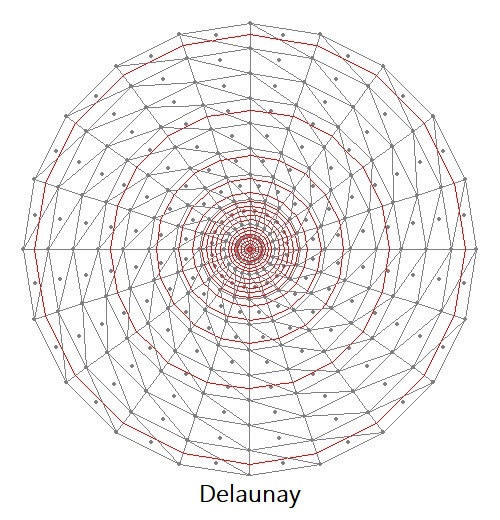
Then hardly any difference can be observed, except - as has been argued at nauseum - at the boundary.
Yet the approach with Delaunay weighting has to be deemed wrong. I have sent an <NL>email message</NL> to (one of) the authors about the issue. Not surprisingly, they don't answer.
I guess that too much effort has been spent already, making a turnaround virtually impossible.


