Inhoud

Rente door Afschrijving

Een Eigen Huis
HypotheekVormen
TermijnStructuur
Exponentieel Verval
Experimenteel Vergelijk
RisicoSpreiding
Amerikaanse versie
Samenvatting
Bronnen

Gedateerd februari 2003.

Rente door Afschrijving

Bij het voorbeeld van de auto is gebleken dat, nadat het ding veranderd was in schroot, het ruil-equivalent in goud een waarde van nul zou moeten hebben gekregen. Maar omdat goud waardevast is, moet het eenzelfde waarde, in de vorm van interest, weer aan zichzelf hebben toegevoegd. Dat zou in ons geval weer de volle waarde van de auto zijn. Aan deze theorie ontbreekt echter het een en ander. De voornaamste vergroving is dat geld een geheugen zou hebben voor datgene waartegen het is geruild. Dit is natuurlijk niet het geval. Het geld wat gebruikt is bij het kopen van een auto kan niet een andere interest vragen dan het geld wat gebruikt is bij het kopen van een wasmachine, want er bestaat geen verschil tussen auto-geld en wasmachine-geld. Het geld zal geen wetenschap hebben van de afzonderlijke afschrijvingen van de waren. Maar dit neemt niet weg dat er wel degelijk een idee zal bestaan van de afschrijvingen, zoals deze, bijvoorbeeld gemiddeld, in de maatschappij voorkomen. Zonder een dergelijk Weten zou het Geld namelijk geen enkel middel hebben om te bepalen wat zijn rentevoet moet zijn. Om te beginnen moet deze zodanig hoog liggen dat, bij een bovengemiddelde levensduur van het goed, de volledige hoofdsom van desbetreffende lening nogmaals kan worden vergoed. Verder bestaat er een zogenaamde rente termijnstructuur, dat is het verloop van de rentevoet als funktie van de looptijd. Een goede theorie over Rente door Afschrijving zal in staat moeten zijn om voor deze termijnstructuur een verklaring te vinden.

Een Eigen Huis

De eerste onderzoeksvraag kan als volgt worden geformuleerd. Bestaat er een goed met een meer-dan-gemiddelde levensduur - dit zal geen auto zijn - zodanig dat het geld namelijk de volle waarde van het goed kan terugverdienen, in de vorm van interest over een langlopende lening ? Iedereen die zelf wel eens een huis heeft gekocht, is maar al te zeer bekend met een dergelijk goed. Wie ooit een hypotheek op zijn huis heeft afgesloten, weet dat hierbij een rol wordt gespeeld door de volgende grootheden: de betalingen, de rentevoet en de looptijd. Er zit nog een addertje onder het gras met betrekking tot de looptijd. Zonder een telefoontje met een zwager van mij - iemand die goed thuis is in het financiële gebeuren - was ik niet te weten gekomen dat de looptijd van de lening eigenlijk ook de tijd is waarin het huis, vreemd genoeg, voor de bank, wordt afgeschreven. Dit is met name duidelijk voor bedrijfsgebouwen, die inderdaad in 30 à 40 jaar schijnen te worden afgeschreven. Hoe het ook zij, de konklusie is in ieder geval dat we de looptijd mogen identificeren met een tijd van afschrijving. Dit geldt ook voor woonhuizen.
Door de meest omstreden fiscale maatregel aller tijden in Nederland, onze hypotheekrente aftrek, wordt in belangrijke mate versluierd hoeveel rente eigenlijk aan de geldschieter moet worden betaald. In feite zijn het natuurlijk de belastingbetalers, u en ik, die meehelpen om water naar de zee (= de bank) te dragen. Vanwege de aftrek is iets beter te begrijpen dat veel huiseigenaren niet beseffen hoeveel de totale, aan de bank afgedragen rente eigenlijk bedraagt. Ik kan het u precies vertellen: minstens evenveel als de hoofdsom. De bank incasseert dus het volle bedrag van de schuld nog een keer opnieuw. Wie dit niet gelooft, nodig ik uit om het voor de eigen situatie een keertje na te rekenen. Maar vergeet niet waar het ons in deze en de volgende paragraaf om gaat: we willen aantonen, aan de hand van woonhuizen als voorbeeld, dat de rente op de vrije markt op een dusdanig hoog niveau ligt, dat ze (groter of) gelijk is aan de totale waarde van een duurzaam goed, gerekend over de periode van afschrijving.
De wijze waarop het volle bedrag van de schuld nogmaals wordt geïncasseerd hangt af van de hypotheekvorm. In de tijd toen ik zelf een huis kocht lagen de zaken nog tamelijk eenvoudig. Er bestonden maar twee hoofdvormen: de lineaire hypotheek en de annuïteiten hypotheek. In mijn rekenmodellen hiervan ga ik iets doen wat in de financiële wereld niet de gewoonte is, maar wat mij (als theoretisch fysicus van huis uit) goed bevalt. Ik ga namelijk continue modellen maken van de discrete formuleringen welke bij de banken in zwang zijn. De bedoeling hiervan is om geen hinder te hebben van de verschillende betalingstermijnen, of die nu gerekend worden in weken, in maanden of in jaren ... of in seconden.

HypotheekVormen

Het nu volgende betoog is nogal technisch en de links zijn alleen bedoeld voor degenen onder ons die niet bang zijn voor een beetje wiskunde.
De volgende symbolen worden in dit verband gebruikt: v = rentevoet, rente per geleend bedrag per tijdseenheid ; T = looptijd van de lening .
Om te beginnen de lineaire hypotheek. We zijn geïnteresseerd in het geval dat de rente groter of gelijk is aan de volledige hoofdsom.
Dit blijkt te zijn voor rentevoet maal looptijd groter dan twee of: v.T > 2 . Men zou de faktor 2 kunnen betitelen als een grenswaarde, waarboven het voor de bank "nut" heeft om de hypotheek te verstrekken, een soort van grensnut (Dit is niet wat in de traditionele economie onder grensnut wordt verstaan, maar wij vinden de term te toepasselijk om hem hier niet te gebruiken) Nemen we een looptijd van 30 jaar, dan wordt voor dit break-even point gevonden een rentevoet van 2 / 30 = 6,7 % . Dit betekent dat een lineaire hypotheek, bij deze rentevoet, in staat is de volledige hoofdsom nog een keer helemaal terug te verdienen.
Bekijken we nu de tweede hypotheekvorm: die van de annuïteitenhypotheek. De formules zijn veel ingewikkelder. Daarom worden ze eveneens op een aparte bladzijde behandeld. De uitkomst van al deze berekeningen is echter eenvoudig te begrijpen. We vinden voor de annuïteiten-hypotheek namelijk een soortgelijke grensnut-formule als voor de lineaire hypotheek, alleen met daarin een andere konstante, om precies te zijn: v.T > 1.59362426 . Met andere woorden. Door het verstrekken van een annuïteiten-hypotheek is de bank in staat de volledige hoofdsom aan rente terug te verdienen, zodra het produkt van looptijd en rentevoet groter is dan de waarde = 1.6 ( die is < 2 ) .
We zien dat een annuïteiten-hypotheek in dit opzicht "efficiënter" is, want men kan volstaan met een kortere looptijd en/of een lagere rentevoet dan bij de lineaire hypotheek. Om de gedachten te bepalen. Bij een looptijd van 30 jaar is de hypotheek "rendabel" voor een rentevoet groter dan 1.59362426 / 30 = 5,3 %. Een en ander wordt wonderwel bevestigd door een bijna toevallige passage in het boek 'Interest and Inflation Free Money' van Margrit Kennedy [ 4 ] . Hier staat namelijk, tussen haakjes: costing on the average 5 % annual maintenance costs, which is exactly what has been paid in the form of interest for money throughout history. Nooit geweten dat een huis zoveel vergt aan "onderhoud" !
Maar in de tegenwoordige tijd zijn beide hypotheekvormen, zowel de lineaire als de annuïteiten-hypotheek, een beetje "uit". In plaats hiervan zijn andere vormen van hypotheekverstrekking ontstaan, waarbij varianten op de zogenaamde BeleggingsHypotheek de belangrijkste zijn. De verklaring voor dit verschijnsel wordt gevormd door de lage rentestand. Deze is namelijk gedaald tot beneden wat wij hebben aangeduid als minimale waarden, waarboven pas de hoofdsom kan worden terugverdiend. De lange rentestand bereikt tegenwoordig gemakkelijk waarden onder de 5,25 % en zelfs minder dan 4,7 % (5-jaar vaste termijn). Dit is een stuk minder dan de minimale 5,3 % welke nodig zou zijn om een annuïteitenhypotheek "normaal" te laten functioneren. Reden waarom er wordt uitgeweken naar Beleggen op de Beurs, want het geld moet en zal toch ergens "voldoende" interest opbrengen.

TermijnStructuur

Een belangrijk onderwerp binnen de traditionele economie is de zogenaamde Rente TermijnStructuur. Hiermee wordt bedoeld het verband tussen de looptijden en de rentevoet van leningen op een bepaald tijdstip (en in een bepaald land). Als voorbeeld kan genomen worden de termijnstructuur van de rente in de Verenigde Staten in augustus 1953, zoals weergegeven in de inaugurele rede van P.A.Bekker: 'Eenvoud en Verwarring rond Optieprijzen' (inmiddels verdwenen van het Web). Verticaal zijn rentevoeten uitgezet die corresponderen met [ ... ] looptijden, die horizontaal zijn uitgezet. Ik heb de betreffende figuur voor het gemak maar even overgenomen (en dat is maar goed ook):

Vlak voor de afsluiting van zijn oratie laat Bekker zien dat het verband tussen rente en termijnen goed beschreven kan worden door een bepaald rekenmodel. Als we vervolgens een zoekmachine in werking zetten, dan blijkt al ras dat Bekker's benadering bij lange na niet de enige is. In het Nederlandse taaldomein krijgt men met rente termijnstructuur slechts een zevental referenties, maar in het Engelstalige domein met "interest rates" "term structure" meer dan het duizendvoudige hiervan !
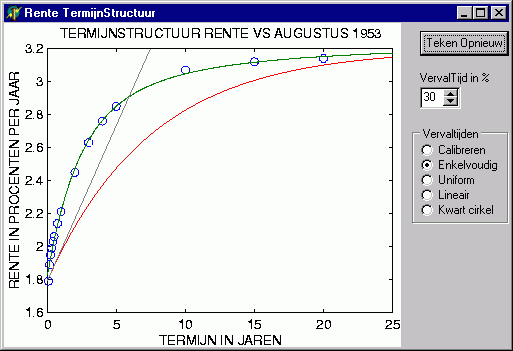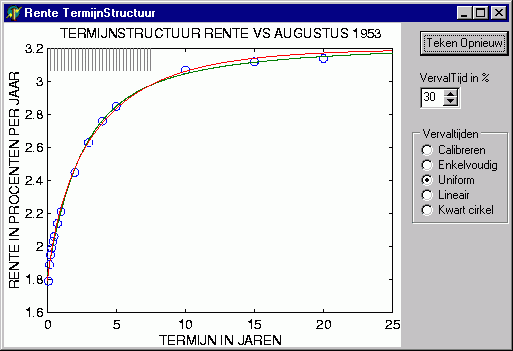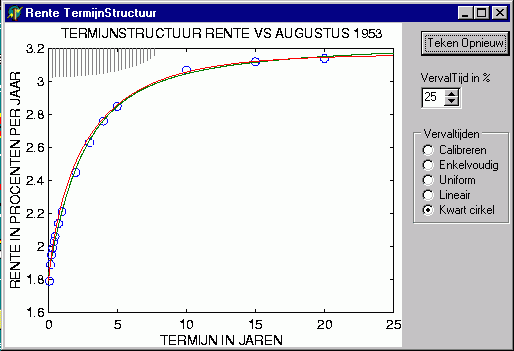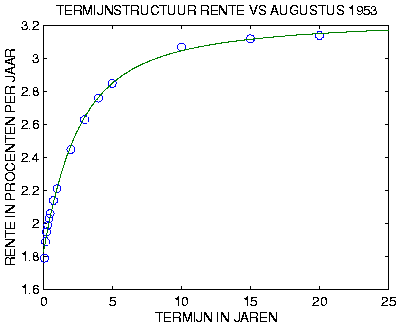
Het hoeft geen verwondering wekken dat waar gesproken wordt van "interessant", onze economen het hebben over financieel interessant, over rendabel in de zin van goed voor het eigen gewin. Dit is dan ook de belangrijkste motivatie achter het onderzoek naar goede modellen om de rente termijnstructuur te beschrijven. Teken aan de wand is dat onze economen er tot nu toe niet in geslaagd zijn tot een geslaagde afsluiting van dit onderwerp te komen. Ondanks alle inspanning. Deze indrukken worden bevestigd bij het lezen van de (inmiddels achter Blackboard verdwenen) 'CollegeNotities' van een ter zake deskundige: Veel studies laten zien dat de theorie in de praktijk vaak slechte uitkomsten geeft. Voorspellingen met de termijnstructuur van toekomstige rentes zijn slecht en soms systematisch fout.

Wij hebben de motivatie dat een verband tussen rente en termijnen "rendabel" zou moeten zijn in het geheel niet. Dit maakt dat het eigen onderzoek kan worden gedaan vanuit een positie die, wat dit aangaat, een stuk comfortabeler is. Van de andere kant rust er een zware bewijslast op degene die durft te beweren dat rente = afschrijving. Want het is duidelijk, voor wie even nadenkt, dat de rente termijnstructuur hier zeker mee te maken moet hebben. We stellen ons dus tot doel de rente termijnstructuur, althans voor een groot gedeelte, te verklaren vanuit het idee dat rente te maken heeft met de globale afschrijving van goederen.

Exponentieel Verval

Ook het nu volgende betoog is nogal technisch. Er bestaat een gedegen wiskundige theorie over de levensduur van materiële zaken zoals machines. Nauwkeuriger geformuleerd. Bekend is dat het kapot gaan van dingen heel vaak goed beschreven kan worden door een exponentiële distributie of kansdichtheidverdeling: f(t) = e^-t/τ / τ .
Hierin is τ = de gemiddelde tijd tussen het falen van het een en het ander, of de tijd dat het gemiddeld duurt voordat voor de eerste keer iets kapot gaat. τ wordt kortweg genoemd de halveringstijd of vervaltijd. Er zijn veel referenties op het Web te vinden, zelfs als er wordt gezocht met een wat overdreven gedetailleerde trefwoordenlijst, zoals: exponential probability distribution failure. In sommige artikelen vindt men elementaire uitleg. Er wordt met name gezegd dat, wegens de eenvoud ervan, de exponentiële distributie veelvuldig wordt gebruikt, ook in gevallen waarin toepasselijkheid niet gegarandeerd is. Dit is precies wat we nu gaan doen. We verklaren de exponentiële distributie namelijk van toepassing op de kans dat een willekeurig produkt in een land kapot gaat. Anders gezegd, we nemen aan dat de kansdichtheid van de afschrijving van alle goederen in een land, als eerste goede benadering, een exponentiële distributie is. De gemiddelde levensduur van deze goederen wordt, als dit het geval is, gegeven door de enige parameter van deze distributie: τ . En de ontwaarding van de goederen als funktie van de tijd, in het bereik van nul tot honderd procent, wordt gegeven door de cumulatieve verdeling: W(t) = ₀∫^t e^u/τ / τ du = 1 - e^t/τ
De termijnstructuur van de rente kan nu worden gerelateerd aan de cumulatieve verdeling van de afschrijvingen als volgt. We hebben gezien dat het Geld kennis moet hebben van de afschrijvingen, want anders zou niet bekend zijn hoe de rentevoeten moeten worden ingesteld. We preciseren dit nu door te stellen dat de termijnstructuur van de rente gelijkvormig zal zijn met de cumulatieve verdeling voor de afschrijvingen. Het argument hiervoor is dat de rente als risico-premie gelijk op zal lopen met het risico dat een artikel uit het assortiment de geest geeft. Uitgedrukt als percentage van de hoofdsom wordt dit dus dezelfde formule, gecorrigeerd met een verschuiving en een schaalfactor, zodanig dat het hele verloop is ingeklemd tussen de rentevoet voor de korte termijnen en de rentevoet voor de lange termijnen. Noem de eerste v_k en de laatste v_L. Tenslotte is het zo dat de rentevoet niet varieert met de tijd (t) van het leven, maar met de looptijd (T) van een lening. Dan wordt de gehele voorstelling van zaken uitgedrukt door de volgende, wonderlijk eenvoudige formule: v(T) = v_k + ( v_L - v_k ) ( 1 - e^T/τ )
In woorden: de rente termijnstructuur is een basis-rentevoet (LiquiditeitsPremie / GrondRente) plus het verschil tussen de lange en korte termijn rentevoet maal het risico dat de afschrijvingen vormen (RisicoPremie). Zoals gebruikelijk bij mathematische modellen, kan deze formule alleen maar zo eenvoudig zijn omdat er slechts een eerste benadering is gemaakt. Zo'n wiskundig model is slechts een ruwe schets van de werkelijkheid en anders niet.

Experimenteel Vergelijk

Een vergelijk van de theorie met de praktijk zou met name enige informatie moeten kunnen verschaffen over de grootte van de gemiddelde tijd τ van afschrijvingen in onze maatschappij, want deze grootheid is voor ons uitermate interes(t)sant om te weten te komen.
Uitgaande van de grafiek van Bekker kan men de rentevoet van de lange en korte termijnen gemakkelijk aflezen: v_L = 0.032 , v_k = 0.018 . Een schatting van de halveringstijd ofwel de vervaltijd τ kan in eerste instantie worden verkregen door te kijken naar de rentevoet van de lange termijnen. De halveringstijd moet in ieder geval kleiner zijn dan de tijd die met v_L overeenkomt. Dit geeft ons een bovengrens voor de vervaltijd; deze is: τ = 1/V = 1/0.032 = 31 jaar en 3 maanden. (Dit is maar een paar jaar langer dan de 25 jaar welke de grafiek breed is.) De werkelijke vervaltijd zal weliswaar in deze orde van grootte liggen, maar zal, in plaats van de volle mep, een percentage hiervan bedragen, laten we eens 30 procent van 25 jaar nemen. Dit komt neer op een globale levensduur van gemiddeld genomen 7.5 jaar. Brengen we nu ons theoretische resultaat in beeld als een rode lijn, bovenop de grafiek van Bekker, dan is de gelijkenis overeenkomstig datgene wat van een ruw wiskundig model mag worden verwacht. De lezer kan zelf nog wat verder experimenteren met het (te downloaden) programma wat voor het maken van deze grafiek is gebruikt. De bijbehorende Delphi broncode is eveneens op te halen. Vergeet niet dat de grafiek van Bekker hierboven dienst doet als (BMP file) invoer voor het programma: dus eerst Opslaan als zodanig. Ophalen kan ook, via deze weg.

Globale schattingen van de levensduur van spullen kan men ook bekomen door (op Internet) te zoeken naar artikelen waarin de kreet "rente en afschrijving" voorkomt, of in het Engels / Amerikaans: "interest and depreciation". Dit levert paar duizend referenties op. (Tussen haakjes: daarentegen levert een zoekterm als "interest by depreciation" nog niet één referentie op. [ Echter, sinds de publicatie van deze webpagina's, zijn ze wel degelijk te vinden ] ) Interessant in dit verband was een artikel waarin staatjes waren opgenomen met daarin rente en afschrijving (1998) van de luchtvaart-industrie in Europa. Men zag dat rente en afschrijving elkaar niet zo heel erg ver ontlopen, grosso modo bezien. In een van de grafieken stond een Europees gemiddelde vermeld van 22 % per jaar. Hiervan bestond ongeveer de helft uit interest en de helft uit afschrijving. Neem voor het gemak 11 % afschrijving, dan zou dit duiden op een levensduur van 9 jaar voor een vliegtuig. Omdat rente en afschrijving ongeveer gelijk zijn, zou dit duiden op eenzelfde gemiddelde tijd van afschrijving: ongeveer 9 jaar (in 1998). Dit zijn Europese toestanden. De afschrijvingen in de US, met de gevonden vervaltijd van 7.5 jaar, lijken door de bank genomen wat korter. Een veilige slotsom lijkt dat de vervaltijden in de Westerse wereld onder de 10 jaar liggen.