Latest revision 02-03-2023 $ \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} \def \SP {\quad ; \quad} \def \MET {\quad \mbox{with} \quad} \def \half {\frac{1}{2}} $

MOND = UAC

Galaxy project
continued

By: Han de Bruijn

From the content of the previous section we must conclude that there is no reason to believe in a Deficient Reasoning for Dark Matter in Galaxies. Does that mean that evidence for dark matter in galaxies is substantial instead? Yes and no! As we shall shortly see, there is an alternative: Arp's Hypothesis. It sounds like: The rest mass of atomic particles is increasing with (proper) time. If this is true, then dark matter apart from common matter may not be much of an issue. Varying elementary particle rest mass can be conceived as dark mass in diguise. Dark matter is not outside but it rests inside common matter.
The basic ideas of this theory have been formulated by Halton Arp, mainly in common speech. Responsibility for the mathematics of Halton Arp's Theory, formulated on this website as Unified Alternative Cosmology (UAC), is mine.

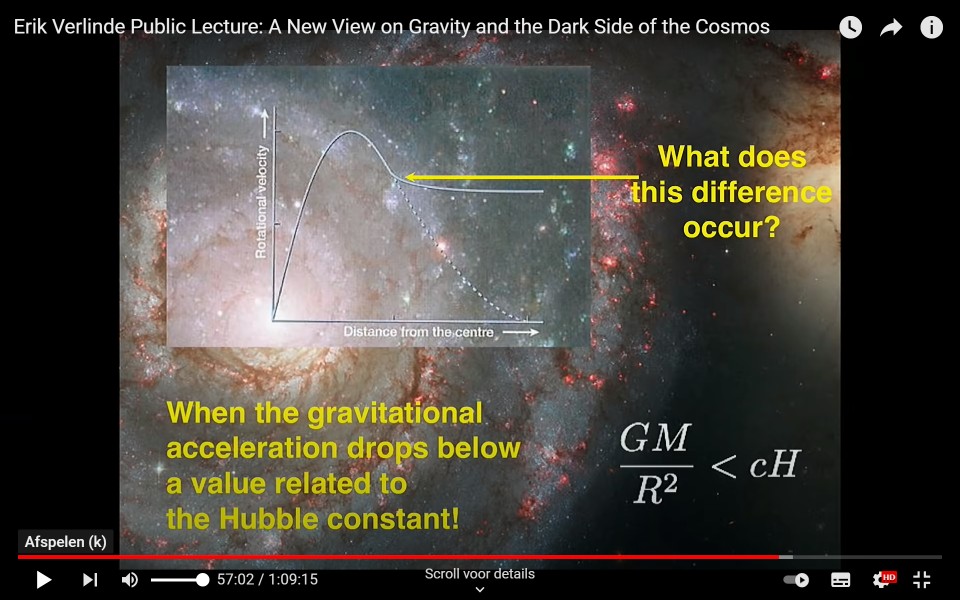
Let's present a little appetizer before we start. Quite unexpectedly, the story below is somehow motivated by an Erik Verlinde Public Lecture: A New View on Gravity and the Dark Side of the Cosmos. At timestamp 56:56 / 1:09:15 an interesting formula is displayed at the slides screen:

Translated into our own terms we infer: $$ \frac{GM}{R^2} \lt cH \hieruit \mbox{number} = \sqrt{\frac{G.W}{c_0H_0}}/L \lt 1 $$ Let's calculate that dimensionless number (with Maple 8). It turns out that it is very near to unity: 

# 1 megaParsec
Mpc := 3.08567758*10^22;
# Hubble constant (2022-02-08)
hubble := 73.4*1000/Mpc;
# Gravity constant (G)
G := 6.67408*10^(-11);
# Speed of light
light := 299792458;
# Number of seconds in a year
year := 31556926;
# Radius of milky way (L)
radius := 52850*light*year;
# Mass of our sun
sun := 1.989*10^(30);
# Mass of milky way (W)
mass := 1.5*10^(12)*sun;
# According to Erik Verlinde
number := sqrt(G*mass/(light*hubble))/radius;
                        
                         number := 1.056854571
Out of sheer curiosity: 
light*hubble;
                                         -9
                          0.7131259132 10
Which is quite close to the Pioneer anomaly: an extremely small acceleration towards the Sun, of $\,(8.74 \pm 1.33)\times 10^{-10}\;m/s^2\,$.
Whatever. As is well known, the Hubble constant is inversely proportional to the age of the universe according to the Big Bang Theory. However, the above means that the radius of the milky way can be calculated with reasonable accuracy by knowing the Hubble constant, the speed of light and the total mass of the galaxy. Translated into own terms it thus may be that the Hubble constant instead is a measure for the age of the matter at the outer boundary of the milky way. Remember that in UAC the "universe" is infinite in space and time, there is no Big Bang.

In view of more recent developments, made explicit in the Origin of Inertia section of UAC, a newly found formula for the Hubble parameter will be distorted as follows. $$ H = \sqrt{\chi\,G\,\rho_0} \MET \chi = \frac{4\pi}{3} $$ and $\rho_0=$ mass density. Let us assume that the galaxy is an ellipsoid, a prolate spheroid to be precise. It's main axes are $\,R\,$,$\,R\,$ and the "radius of the universe" $= c/H\,$. Then we have, in Erik Verlinde's original notation: $$ H^2 = \frac{4\pi}{3} G\,\rho_0 \MET \rho_0 = \frac{M}{4/3.\pi.R^2.c/H} \hieruit \frac{GM}{R^2} = cH $$ Near the bottom of page 1203 in The Case for a Hierarchical Cosmology we read about the old concept that nebulae are "island universes".

More about Erik Verlinde's work is found in Wikipedia: Entropic_gravity.

Unified Alternative Cosmology (UAC)

Once we have gathered some knowledge of UAC, the basics of calculations done before may be reconsidered properly: $$ v^2(r) = \frac{G.W}{V^2.L} \int_0^1 \left[ 2 \int_0^\pi \frac{\left[(r/R)-\cos(\phi)\right]\,d\phi}{\left[(r/R)^2-2(r/R)\cos(\phi)+1\right]^{3/2}} \right] (r/R)\,\rho(R)\;dR $$ Here $G$ is the gravitational constant, $V$ is the reference velocity of a star in the galaxy, $L$ is the radius of the galaxy and $W$ is its total mass, turning $G.W/(V^2.L)$ into a dimensionless constant. As has been calculated elsewhere, the value of it for our own milky way is approximately $\approx 6.4$.
Lower case letters $v,r,\rho$ denote dimensionless variable quantities, preferrably with values between zero and unity.
Corresponding values of speed and distance in standard units may be re-calculated as: $v:=V.v$ , $r:=L.r$ .
Empty space and mass are the only things that are involved with the right hand side. This is what we know from Time Dilation: But the left hand side is different: space and time are involved with $v$. Empty space (e.g. radius) is insensitive to varying elementary particle rest mass, but we have seen that such is not the case with time. It is clear that speed is the derivative of a distance in empty space to time in Newtonian mechanics, which then must be orbital time $T$. This is not how time is observed in astronomy, though. Spectral data are abundant there, that's one reason why. Moreover, according to modern definitions for space and time measurement, time is measured nowadays as atomic time.
Question is: How can astronomers measure the rotation of a spiral galaxy? Google says: The most accurate method to measure the rotation curves of galaxies is to observe the Doppler shift of the 21-cm line emitted by the interstellar hydrogen gas with radio telescopes. With other words: the real measurement result is nothing else than a redshift, and according to standard astronomy it is commonly interpreted as a Doppler shift. So yes, we are actually able to measure the redshift across a galaxy. It should be possible to come up with a precise profile of changing elementary particle rest mass, as a function of the distance $r$ to the center. Below is a beautiful picture of a galaxy. Is it suggesting something of the kind?

An active galactic nucleus (AGN) is a compact region at the center of a galaxy that has a much-higher-than-normal luminosity over at least some portion of the electromagnetic spectrum with characteristics indicating that the luminosity is not produced by stars. The Wikipedia webpage about Non-standard_cosmology says the following at the end of the linked section. Halton Arp has proposed an explanation for his observations by a Machian "variable mass hypothesis". The variable-mass theory invokes constant matter creation from active galactic nuclei, which puts it into the class of steady-state theories. With the passing of Halton Arp, this cosmology has been relegated to a dismissed theory. Dismissed? At Halton C. Arp - The Official Website. Articles we find A Symposium on Active Galactic Nuclei - One Astronomer's View. The article speaks for itself.

Let the velocity in atomic time $t$ be the desired end-result, then without Halton Arp's Theory nothing will happen. But if varying elementary particle rest mass is involved, then according to UAC, things are different. So a reasonable question is: have we been overlooking something? Yes we have! We have been mislead by an uttering from de Sitter as has been quoted in Milne's Formula: There is nothing in our experience of the physical world that would enable us to distinguish between the times $\,t\,$ and $\,T\,$. This statement shall be proven wrong all over the place.
Let $\vec{s}$ be the position vector, $\vec{u}$ be the velocity with atomic time (t) and $\vec{v}$ be the velocity with orbital time (T), then we have, according to the laws of Time Dilation: $$ \vec{u} = \frac{d\vec{s}}{dt} = \frac{d\vec{s}}{dT}\frac{dT}{dt} = \vec{v} \frac{\sqrt{m_0/m}}{m_0/m} = \vec{v} \sqrt{m/m_0} $$ If elementary particle rest mass is varying across the galaxy, then the above correction should be applied to the calculated velocities, in order to represent the observed velocities. Let us assume for a while that elementary particle rest mass is indeed varying across the galaxy, in such a way that new mass is created in the center and becomes more aged when spiralling in outward direction. As a first attempt to mimick the true Galaxy rotation curve, the following hypothesis has been tried: elementary particle rest mass is proportional to the distance from the center of the galaxy. Formally: $m \sim r$; simply a linear relationship to begin with. Furthermore remember that all of our calculations are dimensionless. Then we finally have: $$ \vec{u} = \sqrt{r}\;\vec{v} \hieruit u = \sqrt{r\;v^2} = \sqrt{r}\;v $$ Where $\vec{u}$ is the velocity with atomic time (t), $\vec{v}$ be the velocity with orbital time (T), $(u,v)$ are the absolute values - named speed - of $(\vec{u},\vec{v})$ and $r$ is the dimensionless distance to the nucleus.
In common speech it reads: $$ \mbox{correct rotation curve} \sim \sqrt{\mbox{distance to nucleus}} \times \mbox{wrong rotation curve} $$ Further motivation for our additional hypothesis comes from Modified Newtonian dynamics, especially the formulas for the deep-MOND regime ($a \ll a_0$): $$ {\displaystyle F_{\text{N}}=m{\frac {\,a^{2}\,}{\,a_{0}\,}}~.} $$ Applying this to an object of mass $\,m\,$ in circular orbit around a point mass $\,M\,$ (a crude approximation for a star in the outer regions of a galaxy), we find: $$ {\displaystyle {\frac {\,GMm\,}{r^{2}}}=m{\frac {\;\left({\frac {\,v^{2}\,}{r}}\right)^{2}\;}{a_{0}}} \quad \Longrightarrow \quad v^{4}=GMa_{0}~,} $$ that is, the star's rotation velocity is independent of $\,r\,$, its distance from the centre of the galaxy - the rotation curve is flat, as required.
In comparison we have, with UAC, for the same crude approximation, that the rotation curve is flat as required, but with a square instead of a fourth power and no free parameter $\,a_0\,$: $$ \frac{GMm}{r^2} = m\frac{v^2}{r} \hieruit v = \sqrt{\frac{GM}{r}} \\ u = \sqrt{r/R}\;v \hieruit u^2 = \frac{GM}{R} $$ Where our dimensionless $\,0 \le r \le 1\,$ is replaced by the real world one, by multiplying it with the galaxy's radius $\,R\,$. Just for fun, let us try to calculate Mordehai Milgrom's factor $\,a_0\,$: $$ \left(u^2\right)^2 \; (\mbox{UAC}) = v^4 \; (\mbox{MOND}) \hieruit \left(\frac{GM}{R}\right)^2 = GM\,a_0 \hieruit \\ a_0 = \frac{GM}{R^2} $$ Milgrom's constant - as it appears in UAC - is equal to the standard gravitational parameter divided by the radius squared of a galaxy. The quantities $\,GM\,$ and $\,R\,$ have been determined before, so we just have to continue a previous calculation (see above): 

a_0 := G*mass/radius^2;
                                             -9
                       a_0 := 0.7965199875 10
So we have $\,a_0 \approx 8.0 \times 10^{-10}\mathrm {ms} ^{-2}\,$, while Milgrom found ${\displaystyle \,a_{0}\approx 1.2\times 10^{-10}\mathrm {ms} ^{-2}\,}$ to be optimal. In the original MOND theory the free parameter $\,a_0\,$ is conceived as being a constant and our equality $\,a_0=GM/R^2\,$ is replaced by inequalities. It is perhaps (not) relevant to notice that $\,a_0\,$ is of the same order of magnitude as the (also previously calculated) Pioneer anomaly $\approx c_0 H_0\,$. And it's not a great miracle that this fact has been observed in true MOND theory as well: take a look at formula (2) in the PDF. Perhaps the Pioneer anomaly subsection in Origin of Inertia is interesting too.

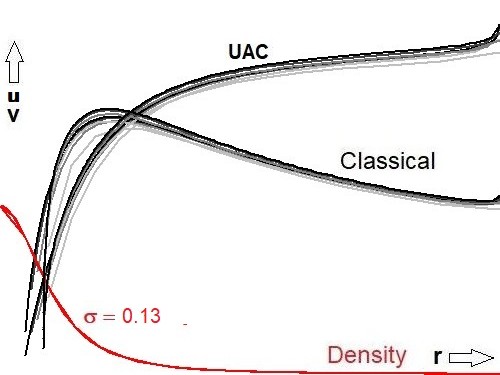
Our end result has been obtained by adapting too the value of the width $\sigma =$ Sigma of the mass density distribution: $\sigma = 0.10 \to \sigma = 0.13$. Let's repeat what's all about. A reference is this one, on page 19: $$ \rho(R) = C\,\left[1+(R/\sigma)^2\right]^{-3/2} \MET 0 \le R \le 1 \quad \mbox{and} \quad \sigma = 0.13 $$ So there is scaling factor ($1/C$) involved, namely the one that norms the mass of the galaxy to unity, according to $\int_0^1 \rho(R)\cdot2\pi R\,dR = 1$. By hand we calculate: $$ C = \int_0^1 \left[1+(R/\sigma)^2\right]^{-3/2}\cdot 2\pi R\,dR = \pi\sigma^2 \int_0^1 \left[1+(R/\sigma)^2\right]^{-3/2} d\left[1+(R/\sigma)^2\right] = \\ \pi\sigma^2 \int_1^{1+1/\sigma^2} y^{-3/2} dy = -2\pi\sigma^2 \left[y^{-1/2}\right]_1^{1+1/\sigma^2} = 2\pi\sigma^2 \left[1 - \frac{1}{\sqrt{1+1/\sigma^2}}\right] = \\ 2\pi\sigma^2 \frac{\sqrt{1+1/\sigma^2}-1}{\sqrt{1+1/\sigma^2}}\frac{\sqrt{1+1/\sigma^2}+1}{\sqrt{1+1/\sigma^2}+1} = \frac{2\pi}{\sqrt{1+1/\sigma^2}\left[1+\sqrt{1+1/\sigma^2}\right]} $$ Giving at last: $$ \rho(R) = \frac{1}{C}\,\left[1+(R/\sigma)^2\right]^{-3/2} \MET C = \frac{2\pi}{\sqrt{1+1/\sigma^2}+(1+1/\sigma^2)} $$ One reason why the result is repeated here is that there may be an error in the scaling factor $C$ with a previous - and herewith declared deprecated - implementation of our app.
A further complication is that there is another scaling factor now for the UAC result, due to the fact that according to our model all elementary particle rest mass is assumed to increase in a linear fashion from the center to the outer boundary of the galaxy. As a consequence the total mass (= integral) would be too small, which of course has to be corrected. This means that we have to evaluate the following integral as well: $$ F = \int_0^1 \left[1+(R/\sigma)^2\right]^{-3/2}\,R\,2\pi R\,dR $$ What we shall finally have is a scaling factor $\,1/C\,$ for the classical Newtonian result and a different scaling factor $\,1/F\,$ for the UAC result. It's too difficult to calculate $\,F\,$ by hand, therefore a computer algebra system (Maple 8) is asked for help: 

> p(R) := (1+(R/sigma)^2)^(-3/2);
> c := 2*Pi*int(p(R)*R,R=0..1);
> f := 2*Pi*int(p(R)*R^2,R=0..1);
> C := evalf(subs(sigma=0.13,c));

                          C := 0.09249686077

> F := evalf(subs(sigma=0.13,f));ere 

                          F := 0.02410082965

> gok := (1/F)/(1/C);

                          gok := 3.837911894
The additional scaling factor gok for $\,u^2\,$ with UAC is $\approx 4\,$ times the one for the Classical $\,v^2\,$, hence the square root of it ($\approx 2$) shall be visible as a scaling factor in the end result.

Results

It seems that we are finished now with the nasty details. Here comes again our own graphics result on the left, and, as a comparison on the right, the (seemingly updated) Galaxy rotation curve from Wikipedia. The quantities in the picture on the left are dimensionless, without absolute scaling for $\,r\,$ and $\,v\,$.
I think that the conclusion is clear. The galaxy rotation speed profile $\,u(r)\,$ as calculated with UAC seems to be in concordance with the observations, while the Classical curve $\,v(r)\,$ is deviant. Details shall not be repeated here for convenience, because they can easily be found in what preceded. Remember that the red curve is auxiliary; it is supposed to represent a sensible Density distribution of the matter in the galaxy (and it contains an adjustable parameter $\,\color{red}{\sigma}\,$).

 

The Source Code of the (thus modified) app shall be in the public domain; search for "Unified Alternative Cosmology" in the source.

Louis Marmet via A Cosmology Group (2023 Feb 17): That was in response to many papers published at the time saying that 'flat' rotation curves show that the luminous mass is much less than the gravitational mass. This is false, it's the fast 300 km/s rotation that needs more gravity, not the flat curves. Real velocities can be estimated from the above leftmost picture. The original size of it has been: 

  xmin := 0; xmax := 1;
  ymin := 0; ymax := 2;
And the UAC velocity profile is at approximately 200 out of 500 pixels from the top. 
# As defined in the Source Code:
speed : double = 250000;
# As learned from the picture:
(500-200)/500*2*V = 300,000 m/s
Thus leading indeed to the required "fast 300 km/s rotation" (a bit by coincidence admittedly :-)