But how would this be possible? Haven't we defined just a minute ago that elementary particle rest mass is created at timestamp $T=A\,$?
The only way out of this apparent paradox is to assume once again that orbital time and atomic time are different, so different that
the universe has a beginning Alpha ($A$) in orbital time and it has always existed when measured in atomic time.
Two results from the previous, Time Dilation, are repeated for convenience:
$$
\frac{dT}{dt} = \sqrt{\frac{m}{m_0}} \slechts \frac{dt}{dT} = \sqrt{\frac{m_0}{m}}
$$
Combining this with (our version of) Narlikar's Law, we obtain (trivially assuming that $T \ge A$):
$$
\frac{dt}{dT} = \sqrt{\frac{m_0}{m}} = \frac{T_0-A}{T-A}
$$
Here $T=$ orbital time, $m=$ elementary particle rest mass, $m_0=$ reference mass (here and now),
$T_0=$ gravitational reference time, which is the "nowadays" timestamp, $A=$ gravitational timestamp corresponding
with a beginning (Alpha), at the time when rest mass is created out of nothing.
What we have now is an ordinary differential equation which can be solved easily:
$$
t(T) = C\ln\left(\frac{T-A}{T_0-A}\right)+D
$$
Where $A$ still is the time of creation. $C$ and $D$ are constants to be determined by setting the atomic increment
equal to the orbital increment at the reference timestamp $(0)$:
$$
\left.\frac{dt}{dT}\right|_{T=T_0} = 1 = \frac{C}{T_0-A} \quad \Longrightarrow \quad C = T_0-A
\quad \Longrightarrow \\ t = (T_0-A)\ln\left(\frac{T-A}{T_0-A}\right) + D
$$
Furthermore we must synchronize the clocks at the reference timestamp $(0)$ such that from $t=t_0$ it follows that $T=T_0$ and so $t_0=T_0$:
$$
t_0 = (T_0-A)\ln\left(\frac{T_0-A}{T_0-A}\right) + D = D \quad \Longrightarrow \quad D = t_0 \quad \Longrightarrow \\
\large \boxed{\;t-t_0 = (T_0-A)\ln\left(\frac{T-A}{T_0-A}\right)\;}
$$
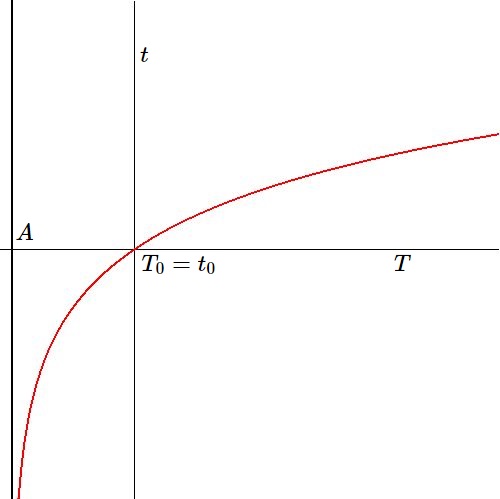
A picture says more than a thousand words. It is clearly seen that orbital time $T$ has a beginning $A$ - Alpha, the moment of creation -
while atomic time $t$ has no beginning, it extends to minus infinite. In addition, both timespans $T$ and $t$ have no ending in our theory.
At last, it should be noticed that

So far so good. But this is what we found on the internet. From Euclid to Eddington: A Study of Conceptions of the External World, by Edmund Taylor Whittaker. From the chapter 19. THE BEGINNING AND END OF THE WORLD:
| Milne | UAC |
| kinematic | orbital |
| dynamical | atomic |
I really don't understand Milne's way of deriving things quite well - and that's an understatement. What to think about the
following utterings in the first reference at the opening page 324, where Milne claims that the laws of
dynamics and the Newtonian approximation to the law of gravitation [ .. ] have been deduced rationally [ .. ] No appeal was
made in the derivations to any empirical laws of dynamics or gravitation, or even to the principle of relativity or to the
principle of the constancy of the velocity of light. No empirical laws?! Okay .. whatever; other titbits of prose from
the same reference are quite worthwhile to consider. But, before doing so, we must complete the relationship between Milne's
formulation and ours.
Last but not least, for the sake of being able to employ a Nondimensionalization (NDM) technique eventually, the Formula shall be slightly rewritten, as follows:
$$
t-t_0 = (T_0-A)\ln\left(\frac{T-A}{T_0-A}\right) \slechts \frac{t-T_0}{T_0-A} = \ln\left(1+\frac{T-T_0}{T_0-A}\right)
\\ \slechts y = \ln(1+x) \MET x = \frac{T-T_0}{T_0-A} \SP y = \frac{t-T_0}{T_0-A}
$$
Then the dimensionless relationship between $\,x\,$ and $\,y\,$ is like in the above picture, with $\,t_0=T_0=0\,$ and
a dimensionless place of the Asymptote $\,=(A-T_0)/(T_0-A)=-1\,$ for $\,x=A\,$.
| Milne | UAC | NDM |
| $\tau = t_0\log\frac{t}{t_0}+t_0$ | $t-T_0=(T_0-A)\ln\left(\frac{T-A}{T_0-A}\right)$ | $y = \ln(1+x)$ |
From which it can easily be derived that:
| Milne | UAC | NDM |
| $t_0$ | $T_0-A$ | |
| $t$ | $T-A$ | $t_0(1+x)$ |
| $\tau$ | $t-A$ | $t_0(1+y)$ |
| $\log$ | $\ln$ |
Now we can quote, with our own notation and interpretation, starting at page 328.
program scheppen;
Uses Algemeen;
procedure test;
const
{ Year of Creation }
A : double = -20000;
{ Year of orbital -> atomic time }
T0 : double = 1967;
var
ta : double; { Atomic time }
Tg : double; { Orbital time }
tv : double;
dag : integer;
weet : string;
begin
Writeln('Creation in gravitation time :',-A:8:0,' year B.C.');
Tg := A; ta := 0; weet := '';
for dag := 0 to 6 do
begin
Tg := Tg + 1/365;
tv := ta;
ta := t0 + (T0-A)*ln((Tg-A)/(T0-A));
if ta-tv < 0 then weet := 'eternal'
else weet := Letterlijk(Round(ta-tv));
Writeln('year B.C. :',-ta:8:0,' | years :',
weet:8,' (end of day ',dag,')');
end;
end;
begin
test;
end.
What can be done is start with the moment of creation $A$(lpha). In the above program Alpha is assumed to be 20,000 B.C. (but other
values can of course be tried). We can not calculate for the corresponding atomic time, however, because it's minus infinity.
No problem, because orbital time is going to be increased with just one day at a time. Calculation defines what comes out for the
atomic time - in years - corresponding with those orbital days. If the program is executed, then the outcome is:
Creation in gravitation time : 20000 year B.C. year B.C. : 347247 | years : eternal (end of day 0) year B.C. : 332020 | years : 15226 (end of day 1) year B.C. : 323113 | years : 8907 (end of day 2) year B.C. : 316794 | years : 6320 (end of day 3) year B.C. : 311892 | years : 4902 (end of day 4) year B.C. : 307887 | years : 4005 (end of day 5) year B.C. : 304501 | years : 3386 (end of day 6)It is noticed that the end of day 6 corresponds rather accurately with the birth of mankind according to Evolution Theory, namely approximately 300,000 years ago. But that's not all. In the Bible it is read that With the Lord a day is like a thousand years, and a thousand years are like a day. (2 Peter 3:8). If we understand this as an order of magnitude, then there is no contradiction too with the outcomes in the second column.
Another exercise, with Maple 8 this time, leads to an alike result. The two clocks - atomic time and orbital time together - are flexible enough to account for (sort of) an astronomic time scale and (sort of) a creationist time scale "at the same time". We took the freedom (again) to identify Atomic time with the Astronomical time scale and Orbital time with the Creationist time scale. It is expected that neither of the parties will object to this choice. All numbers are expressed in years. We have made an educated guess (= trial and error) for the age in Orbital time, in such a way that the beginning of the first creation day shall correspond with the commonly accepted age of the earth, which is $\approx 4.543$ billion years ago. Alas, it doesn't turn out that the earth was created $6,000$ before Christ. Instead we find $\approx 182.3$ million years B.C.
> age := 1.823*10^8;
> day := 1/365.242199;
> for i from 1 to 8 do
> milne[i] := age*ln(i*day/age);
> end do;
> for i from 1 to 7 do
> era[i] := milne[i+1]-milne[i];
> end do;
9
age := 0.1823000000 10
day := 0.002737909263
10
milne[1] := -0.4543230455 10
10
milne[2] := -0.4416869724 10
10
milne[3] := -0.4342953434 10
10
milne[4] := -0.4290508993 10
10
milne[5] := -0.4249829924 10
10
milne[6] := -0.4216592703 10
10
milne[7] := -0.4188491034 10
10
milne[8] := -0.4164148262 10
9
era[1] := 0.126360731 10
8
era[2] := 0.73916290 10
8
era[3] := 0.52444441 10
8
era[4] := 0.40679069 10
8
era[5] := 0.33237221 10
8
era[6] := 0.28101669 10
8
era[7] := 0.24342772 10
Astronomic eras of 100 million years are observed here, with orbital days having a duration of only 24 hours. Just to demonstrate that
embedding creationism in serious science is possible, in principle. I didn't hopefully suggest that we have succeeded already in doing so.
And one other thing should be mentioned that has the potential of spoiling the party altogether.