$
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \SP {\quad ; \quad}
\def \MET {\quad \mbox{with} \quad}
\def \half {\frac{1}{2}}
$
Latest revision 31-10-2022
Galaxy project
By: Han de Bruijn
Jan 2016 / Nov 2019
A standard book about astronomy is:
THE PHYSICAL UNIVERSE
An Introduction to Astronomyby Frank H. Shu
And, according to that standard book, there is the Missing Mass Problem, as explained here:

In my humble opinion - I'm not an astronomer - it's a bit suspect that anything in the distant
cosmos appears to be oversized. And the more distant, the more oversized. It's not impossible that
flaws in the Cosmic Distance Ladder (Wikipedia) are to be hold responsible for this, as is argued in Incorrect Assumptions in Astrophysics. While this might provide an explanation for
the issues (1), (3) and (4) in Box 12.1, it definitely does not clarify issue (2): the flat
Galaxy rotation curves:
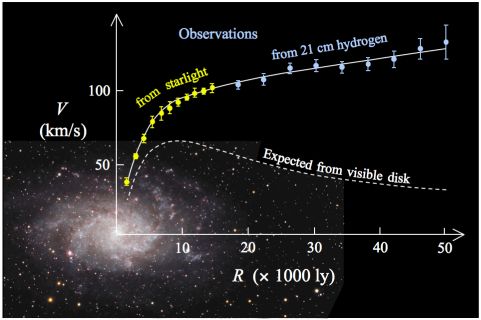
At an alternative website, called
The 100 Year Wrong Turn in Cosmology, we find a
PDF document
with the intriguing title "Galactic mass distribution without dark matter or modified Newtonian
mechanics". It is written by Kenneth F Nicholson, a retired engineer. A more elaborate paper
with analogous content is the PDF titled
"Mass Distribution in Rotating Thin-Disk Galaxies According to Newtonian Dynamics",
by James Q. Feng and C. F. Gallo. A very much improved version of the latter paper is:
Could this be possible? That part of the Missing Mass Problem can be solved by simple and
straightforward application of classical Newtonian mechanics? And that part of the problem has
come into existence solely by erroneous calculation? Seems unbelievable! But anyway, it's
quite worthwhile to check it all out. Now!
According to Newton's law of universal gravitation, the attractive force ($F$) between two bodies
is directly proportional to the product of their masses ($m_1$ and $m_2$), and inversely
proportional to the square of the distance ($r$ : inverse-square law) between them
(see Wikipedia):
$$
F = G\frac{m_1 m_2}{r^2}
$$
The constant of proportionality ($G$) is the gravitational constant:
$$
G = 6.674\,08(31) \times 10^{-11}\,m^3\,kg^{-1}\,s^{-2}
$$
Newton's law of gravitation shall be applied to a RingWorld of gravitating matter, to begin with.
RingWorld Integral
Consider a ring (= circle) with a uniform mass density distribution.
The RingWorld has a center $M$ and a radius $R$:
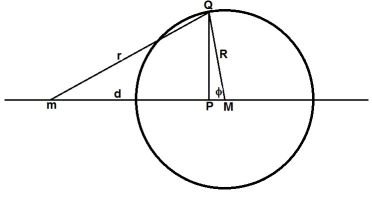
Let $m$ be a test mass at some distance $d$ from the center $M$ of the RingWorld.
Let $Q$ be the position of an infinitesimal element in the Ring.
The mass $m_1$ in Newton's law shall be identified with the test mass $m$.
Let the mass density (with dimension $kg/m^2$) in the (flat) ring be equal to $\rho$.
Then the infinitesimal element at $Q$ has a mass $\rho\,R\,dR\,d\phi$ , to be identified with $m_2$.
So Newton's law becomes, for the gravitational attraction between the test mass and an infinitesimal
part of the ring:
$$
dF = G\frac{m \times \rho\,R\,dR\,d\phi}{r^2}
$$
Where $r$ is the distance between the test mass $m$ and the infinitesimal element at $Q$.
Due to symmetry, straight lines through the center of the ring must be all equivalent.
For simplicity, select the line through the x-axis for measuring forces. Polar coordinates
are to be employed. Furthermore, let $\overline{QP}$ the perpendicular from $Q$ onto $\overline{mM}$.
Then, according to Pythagoras' theorem and some simple trigonometry:
$$
r^2 = (\overline{Mm}-\overline{MP})^2+(\overline{PQ})^2 =
\left[d-R\cos(\phi)\right]^2+\left[R\sin(\phi)\right]^2 \quad \Longrightarrow \\
r^2 = d^2-2Rd\cos(\phi)+R^2
$$
Due to symmetry, we only need to consider the component of the force that is directed from
$m$ to $M$, being a projection:
$$
\overline{Pm}/\overline{Qm} = \frac{d-R\cos(\phi)}{r}
$$
Herewith Newton's law becomes, with $r^3$ in the denominator:
$$
dF = G\frac{m\times\rho\,R\,dR\,d\phi}{r^2} \times \frac{d-R\cos(\phi)}{r} = m \times
G\frac{\rho\,R\,dR\,\left[d-R\cos(\phi)\right]\,d\phi}{\left[d^2-2Rd\cos(\phi)+R^2\right]^{3/2}}
$$
The total attractive force at the test mass, exerted by the ring, is the integral of this.
Due to symmetry, half of the computational effort can be saved.
$$
F = m \times 2 \int_0^\pi
G\frac{\rho\,R\,dR\,\left[d-R\cos(\phi)\right]\,d\phi}{\left[d^2-2Rd\cos(\phi)+R^2\right]^{3/2}}
$$
Make the result dimensionless as much as possible:
$$
F(d/R) = m \times G \rho\,dR/R \times 2 \int_0^\pi
\frac{\left[(d/R)-\cos(\phi)\right]\,d\phi}{\left[(d/R)^2-2(d/R)\cos(\phi)+1\right]^{3/2}}
$$
This formula is valid even for test masses inside the ring: not only for $d > R$
but also for $d < R$. The function $F(d/R)$ is depicted in the figure below. Function value
positive means that the force vector is directed from the left to the right. Function value
negative means that the force vector is directed from the right to the left.
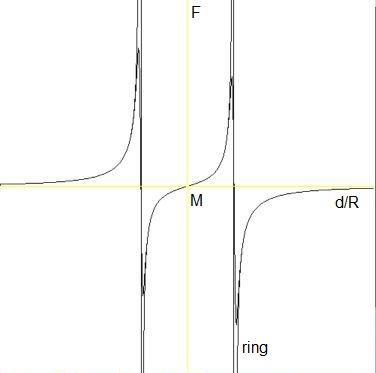
A special case is a test mass at the ring. Then the integral becomes, for $d/R=1$:
$$
F = m \times G \rho\,dR/R \times 2 \int_0^\pi
\frac{\left[1-\cos(\phi)\right]\,d\phi}{\left[1-2\cos(\phi)+1\right]^{3/2}} =
m \times G \rho\,dR/R \times \frac{1}{\sqrt{2}} \int_0^\pi \frac{d\phi}{\sqrt{1-\cos(\phi)}}
$$
Quite unfortunately, this special integral is singular; it has an infinite outcome,
because the denominator of the integrand is zero for $\phi=0$. How do we deal with that?
The answer is that we don't! Take a look at the above graph. If the test mass $m$ is close
to the ring, then it will experience a strong force towards the ring. This simply means that
a test mass cannot escape from its RingWorld. And that's all. A test mass in the ring does
not contribute to anything else than just staying there. Therefore what we shall do is:
simply skip / ignore the infinite contribution.
Mathematical model
Mathematics is not reality. Mathematics is fantasy. But it is tamed fantasy. Once
you have established the basic hypotheses, there is no way out. You have to follow the logic
and accept the consequences, whatever they are right or wrong. So what we shall do now is to
make a mathematical model of a galaxy, knowing that it is of limited validity when compared
with its immense reality. It will be assumed that the galaxy can be modeled as a flat disk.
The flat disk, in turn, is thought as being built up from (in)finitely thin RingWorlds:
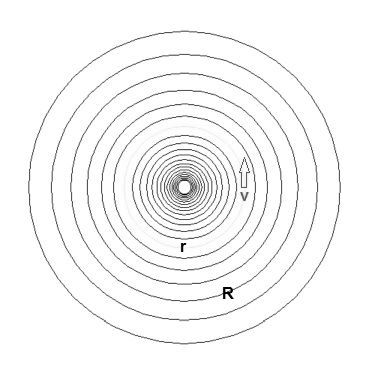
Employing the end result from the preceding section, we first replace $d$ by $r$ - what's in
a name, huh? Then we have, for $\;r/R\ne 1$ and assuming that $\rho(R)$ (the density of the
stars) is a function of the radius only:
$$
F_\mbox{ring}(r,R) = m \times G\,\rho(R)\,dR/R \times 2 \int_0^\pi
\frac{\left[(r/R)-\cos(\phi)\right]\,d\phi}{\left[(r/R)^2-2(r/R)\cos(\phi)+1\right]^{3/2}}
$$
This result must be integrated (i.e summed) over all rings with radius $R\in[R_0,R_1]$:
$$
F_\mbox{galaxy}(r) = \int_{R_0}^{R_1} F_\mbox{ring}(r,R) = m \times G \int_{R_0}^{R_1}
\left[ 2 \int_0^\pi \frac{\left[(r/R)-\cos(\phi)\right]\,d\phi}
{\left[(r/R)^2-2(r/R)\cos(\phi)+1\right]^{3/2}}\right] \rho(R)/R\; dR
$$
This is the total force exerted by all rings in the galaxy on a test particle in the galaxy.
The test particle is part of the ring with radius $r$. That ring is assumed to rotate with
uniform velocity $v$, thus creating a centripetal force which is opposite and equal to the
gravitational force of the galaxy. The expression for this centripetal force is well known.
Thus we have:
$$
F = \frac{m\,v^2}{r} = F_\mbox{galaxy}(r)
$$
Equating the two shows that the result is independent of the test mass $m$ :
$$
v(r)^2 = G \int_{R_0}^{R_1} \left[ 2 \int_0^\pi
\frac{\left[(r/R)-\cos(\phi)\right]\,d\phi}{\left[(r/R)^2-2(r/R)\cos(\phi)+1\right]^{3/2}}
\right] (r/R)\,\rho(R)\;dR
$$There is one important condition, though: $v^2 > 0$ . So the right hand side must be positive.
Otherwise it would be impossible for the RingWorld to compensate gravity by means of a centripetal
force. Herewith one of the serious limitations of the mathematical model has become
obvious already.
While it is noted that the gravitational force can be wildly negative close to the center of the
galaxy, one thing is for sure: $F_\mbox{galaxy}(r=0) = 0$, so there is no counter force needed
exactly in the center. So far, so good. Now temporary rewrite the same as:
$$
(v')^2 = G \int_{R'_0}^{R'_1} \left[ 2 \int_0^\pi
\frac{\left[(r'/R')-\cos(\phi)\right]\,d\phi}{\left[(r'/R')^2-2(r'/R')\cos(\phi)+1\right]^{3/2}}
\right] (r'/R')\,\rho'(R')\;dR'
$$
The reason is that we want to apply the technique of
Nondimensionalization:
$$
v' = V.v \quad ; \quad r' = L.r \quad ; \quad R' = L.R \quad ; \quad \rho' = W/L^2.\rho
$$
Here $V,L,W$ are quantities with a dimension - velocity, length, mass respectively - and
$v,r,R,\rho$ have now turned into dimensionless quantities, preferrably with values arount unity.
For that purpose, let's say that $V$ is the velocity of the sun in our milky way,
$L$ is the radius of our galaxy and $W$ is its total mass. Substitution leads to:
$$
(V.v)^2 = G \int_{R_0/L}^{R_1/L} \left[ 2 \int_0^\pi
\frac{\left[(r/R)-\cos(\phi)\right]\,d\phi}{\left[(r/R)^2-2(r/R)\cos(\phi)+1\right]^{3/2}}
\right] (r/R)\,W/L^2.\rho(R)\;L.dR
$$
Finally leading to a completely dimensionless expression for the velocity (squared):
$$
v^2 = \frac{G.W}{V^2.L} \int_0^1 \left[ 2 \int_0^\pi
\frac{\left[(r/R)-\cos(\phi)\right]\,d\phi}{\left[(r/R)^2-2(r/R)\cos(\phi)+1\right]^{3/2}}
\right] (r/R)\,\rho(R)\;dR
$$
Let us check that $G.W/(V^2.L)$ is indeed a dimensionless number:
$$
[G] = m^3\,kg^{-1}s^{-2} \SP [W] = kg \SP [V] = m\,s^{-1} \SP [L] = m \\ \hieruit
\frac{[G][W]}{[V^2][L]} = \frac{m^3\,kg^{-1}s^{-2}.kg}{(m\,s^{-1})^2m} = 1
$$
An order of magnitude of this dimensionless constant - for our own milky may - may be calculated
(with Maple 8):
# Gravity constant (G)
G := 6.67408*10^(-11);
# Speed of light
light := 299792458;
# Number of seconds in a year
year := 31556926;
# Radius of milky way (L)
radius := 52850*light*year;
# Mass of our sun
sun := 1.989*10^(30);
# Mass of milky way (W)
mass := 1.5*10^(12)*sun;
# Speed of sun (V)
speed := 250000;
# Dimensionless number
G*mass/(radius*speed^2);
6.372018778
At this stage in the project, it is not quite important though, because we are only interested in
velocities relative to each other.
Results
It's virtually impossible to calculate the Galaxy Integral analytically. Therefore an application
has been developed - formerly called "computer program", nowadays called "app". It's written in
the (Delphi) Pascal programming language. The app shall be in the public domain and it is
accompanied by CopyLefted
A significant detail is: how to design a proper computational grid? I have cooked up two flavors
of them:
- Arithmetical grid.
In radial direction: $R = (i+1)/(N+1)$ with $i = 0,1, \cdots ,N$.
In angular direction: $\phi = j\cdot 2\pi/M$ with $j = 0,1 \cdots , M-1$.
- Geometrical grid.
Much more complicated, as is explained in a separate webpage.
Both grids have been refined a couple of (4) times, doubled to be precise: $N := 2\times N \; ;
\; M := 2\times M$. The more refined the grid, the more black (less grey) the accompanying graph
of the star speed profile $v(r)$. It's a nasty habit of mine not to present numerical results
any more fancy than they actually are. Thus to emphasize once more that a mathematical model
is not reality. It may be an advantage, for example, that you can still observe some
of the layout of courser grids (in the grey curves). Together with the fact that the two grids
give slightly different outcomes.
Crucial for success of the calculations is the (observed) mass density profile of the stars
in the galaxy. For a novice in the field, it's not easy to find something sensible
in the references available on the internet. After some search I've decided to take
this one, on page 19. In the figure below, the graph of this function is sketched in
$\color{red}{red}$. There is another scaling factor involved that norms the mass of the galaxy
to unity, according to $\int_0^1 \rho(R)\cdot2\pi R\,dR = 1$. Apart from such minor details,
this is what we finally have in the program:
$$
\rho(R) \sim \left[1+(R/\sigma)^2\right]^{-3/2} \quad \mbox{where} \quad 0 \le R \le 1 \quad
\mbox{and} \quad \sigma \approx 0.1
$$
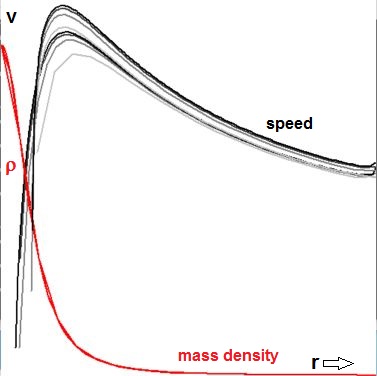

I think that the conclusion is clear. If the adopted mass density profile of the stars is indeed
acceptable, then the galaxy rotation speed profile $v(r)$ is not according to the observations.
This means that I've not yet ( 2016 ) been able to reproduce the claims in the papers by
Kenneth F Nicholson and
James Q. Feng and C. F. Gallo.
Note. These papers
are deviant from the webpage you are reading in that they handle an inverse problem:
how to determine the mass density distribution from a given velocity profile. But still then there is no reason to believe
in a Deficient Reasoning for Dark Matter in Galaxies,
as far as I can see.
Further confirmation for this stand is found at The 100 Year Wrong Turn in Cosmology. Search for "(2010)" and find a (broken) link to the following publication:
Galactic Rotation Described by a Thin-Disk Gravitational Model without Dark Matter.
At least, that's what the title says. In the body of this PDF we are reading something else, though:
However our predicted mass densities show generally slower decaying rates toward the galactic periphery than that of measured
brightness, consistent with more ordinary baryonic mass in the outer disk regions having relatively lower light emissivity
(and thus appearing darker). With other words: NOT without resorting to Dark Matter.
Even more evidence is supplied by L. Marmet and the same C.F. Gallo: Comment on the use of Kepler's laws to describe galactic rotation.
Quote: The excellent data on rotation curves of galaxies and high mass-to-luminosity ratios
provide the main arguments in favour of "matter that has no light".
And in Rotation Dynamics of a Galaxy with a Double Mass Distribution, by Louis
Marmet alone, we read: It is proposed that dark matter does not have to be exotic non-baryonic matter.
Instead, it can be made of molecular hydrogen and condensed matter. Can't resist: it must be condensed milk
then, because we are talking about a milky way, right? Look!
The James Webb Space Telescope shows that
there is spilled milk all over the place (-:
|  |

Whatever. It all simply means: WITH dark matter. It seems to me that there hasn't been accomplished much here.







