Latest revision 27-01-2024

index $ \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} \def \SP {\quad ; \quad} \def \MET {\quad \mbox{with} \quad} \def \half {\frac{1}{2}} $

Seeliger's Paradox

Our key reference is A Paradox of Newtonian Gravitation and Laplace's Solution by Amitabha Ghosh and Ujjal Dey.
Condider a test mass $\,m\,$ at position $(x,y,z)$ inside an infintely large medium with density $\,\rho\,$ (ipse est the universe) and calculate the gravitational force $\,\vec{F}\,$ upon that test mass with Newton's third law. $G\,$ is the Gravitational constant. $$ \vec{F}(x,y,z) = G\cdot m \iiint \begin{bmatrix} x-\xi \\ y-\eta \\ z-\zeta \end{bmatrix} \frac{\rho\,d\xi\,d\eta\,d\zeta}{\left[(x-\xi)^2 + (y-\eta)^2 + (z-\zeta)^2\right]^{3/2}} $$ Introducing a Spherical coordinate system: $$ \left\{ \begin{array}{l} \xi = r \sin(\theta) \cos(\phi) \\ \eta = r \sin(\theta) \sin(\phi) \\ \zeta = r \cos(\theta) \end{array} \right. \qquad \mbox{where} \quad 0 \le \theta \le \pi \quad \mbox{and} \quad 0 \le \phi \le 2\pi $$ Because of the expected spherical symmetry of the problem, we only have to consider a ray in the $\,z\,$ direction, which means that $x=0$ , $y=0\,$. Also put $\,z=R\,$, then we have: $$ d\xi\,d\eta\,d\zeta = r^2dr\sin(\theta)\,d\theta\,d\phi \\ (x-\xi)^2 + (y-\eta)^2 + (z-\zeta)^2 = \xi^2+\eta^2+\zeta^2 - 2 z \zeta + z^2 = r^2 - 2\,r R \cos(\theta) + R^2 $$ The integral then becomes, after some suitable rearrangement: $$ F(R) = G \cdot m \cdot \rho \int_0^{2\pi} d\phi \int_0^\infty r^2 dr \int_0^\pi \frac{\left[R - r\cos(\theta)\right] \sin(\theta) \, d\theta} {\left[r^2 - 2\,r R \cos(\theta) + R^2\right]^{3/2}} $$ Substitute $\,y=\cos(\theta)\,$ and find that $\,dy = \sin(\theta)\,d\theta\,$. Replace $\,y\,$ by $\,(-y)\,$. $$ F(R) = G \cdot m \cdot \rho \cdot 2\pi \int_0^\infty r^2 dr \int_{+1}^{-1}\frac{R-ry}{(r^2-2\,ryR+R^2)^{3/2}} dy \\ F(R) = - G \cdot m \cdot \rho \cdot 2\pi \int_0^\infty r^2 \left[ \int_{-1}^{+1}\frac{R+ry}{(R^2+r^2+2\,ryR)^{3/2}} dy \right] dr $$ At last, substitute $\,x = r/R\,$ to get $$ F(R) = - 2\pi\,G\,\rho\,R\,m\int_0^\infty x^2 \left[\int_{-1}^{+1}\frac{xy+1}{(1+x^2+2\,xy)^{3/2}} dy \right] dx $$ It should be noticed for later use that the distance between the test mass and an infinitesimal element in space $\,= R\sqrt{1+x^2+2\,xy}\,$.
Now calculate the inner integral, the one between square brackets. 
int((x*y+1)/(1+x^2+2*x*y)^(3/2),y=-1..1);
latex(%);
The first line by MAPLE 8, the rest by hand. The outcome is a (Heaviside) step function. $$ -{\frac {-\sqrt { \left( x-1 \right) ^{2}}x-\sqrt { \left( x-1 \right) ^{2}}+\sqrt { \left( x+1 \right) ^{2}}x-\sqrt { \left( x+1 \right) ^{2}}}{\sqrt { \left( x+1 \right) ^{2}}\sqrt { \left( x-1 \right) ^{2}}}} \\ = - \left[-\frac{x}{|x+1|}-\frac{1}{|x+1|}+\frac{x}{|x-1|}-\frac{1}{|x+1|}\right] = \frac{x+1}{|x+1|}-\frac{x-1}{|x-1|} = 1-\frac{x-1}{|x-1|} \\ \\ \hieruit \int_{-1}^{+1} \frac{xy+1}{(1+x^2+2xy)^{3/2}}dy = \begin{cases} 2 \quad \mbox{for} \quad x \le 1 \\ 0 \quad \mbox{for} \quad x \ge 1 \end{cases} $$ It follows that $$ F(R) = - 2\pi\,G\,\rho\,R\,m\left[\int_0^1 2\,x^2\,dx + \int_1^\infty 0\,x^2\,dx\right]= - \frac{4}{3}\,\pi\,G\,\rho\,R\,m $$
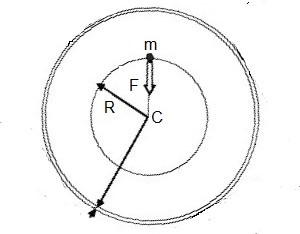
The Paradox of Newtonian Gravitation is in the fact that, according to the above calculations, any test mass $\,m\,$ anywhere in the universe is being attracted (with a force $\,-F\,$) towards the center $C$ of a (spherical) coordinate system, which is also an arbitrary point in the universe. The paradox can be derived in a much simpler way by employing two well known results in gravity theory. Both are a consequence of Newton's Shell theorem. The first result is that the force upon a test mass inside a hollow sphere is exactly zero. The second result is that the force upon a test mass outside a massive sphere is the same as the force towards a point at the center of the sphere with the total mass of the sphere concentrated in it. Therefore the total force is simply $\,F = - G\,m(\rho\cdot 4/3\pi R^3)/R^2 = -4/3\,\pi\,G\,\rho\,R\,m\,$ , quite in concordance with the more elaborate theory.
How can the Paradox of Newtonian Gravitation be resolved? The approach as has been employed by Pierre-Simon Laplace is to modify Newton's third law according to formula (2) in our key reference. $$ F = G\frac{m_1 m_2}{r^2}\exp(-\Gamma r) $$ Let us translate this to our integral. Remember that $\,r = R\sqrt{1+x^2+2\,xy}\,$ in there and abbreviate $\,\Gamma R = \alpha\,$. $$ F(R) = - 2\pi\,G\,\rho\,R\,m\int_0^\infty x^2 \left[\int_{-1}^{+1}\frac{e^{-\alpha\sqrt{1+x^2+2\,xy}}(xy+1)}{(1+x^2+2\,xy)^{3/2}} dy \right] dx $$ Where $\,\alpha = \Gamma R\,$ is a dimensionless quantity, still dependent on the place of the test mass in the universe.
In order to resolve for the paradox, the integral must be zero. The authors of the key reference have presented numerical evidence, but they have not been able to prove this analytically. The latter has become subject of a posting at the Mathematics Stack Exchange forum (MSE for short): Prove or disprove the equality of these two integrals. Employing the power of our favorite computer algebra system (MAPLE 8) - Brain off, computer on! - we find a straightforward shortcut to the proof that $\,F(R) = 0\,$. 
g(x,alpha) := int(exp(-alpha*sqrt(1+x^2+2*x*y))*(x*y+1)/(1+x^2+2*x*y)^(3/2),y=-1..1);
F := int(g(x,alpha)*x^2,x=0..infinity);
simplify(%,assume=positive);
                                  0
Fortunately, there are people on the internet much smarter than me and others. So here comes the proof that I've been waiting for. It's entirely by hand: Brain on, computer off !
The gravitational force on a test mass in a universe with uniform density is zero everywhere. However, this is only the case with "assume=positive". The paradox pops up again as soon as $\,\alpha\,$ is exactly zero. We can see that, at a positive infinitesimal distance from $\,\alpha = 0\,$, the integral suddenly changes from $2/3$ to $0$. Thus $\,\alpha = 0\,$ or $\,\alpha \gt 0\,$ makes a hell of a difference !!

Why am I so motivated by this problem? Take a look at equation (2) in the paper by Amitabha and Ujjal. It's because our version of the Variable Mass Theory (UAC) comes in with Laplace's modification of the law of gravitation. It's reasonable to assume that the test mass $\,m\,$ is located near us, here and now. If the other infinitesimal masses $\,d\mu = \rho\,dV\,$ in the universe are at large distances $\,r\,$ from us, as is usually the case with cosmology, then we are looking backwards in the past $\,(t_0-t)\gt 0\,$ and the corresponding variable masses have been smaller at that time, according to (boxed) formulas in the Hubble Parameter section: $$ \frac{d\mu}{d\mu_0} \large = e^{-H(t_0-t)} = e^{-H/c_0\,\cdot\, r} $$ where $H=$ (intrinsic) Hubble parameter :-(with tension)-: and $c_0=$ speed of light in empty space. It's easy to see now that Laplace's factor must be $$ \exp(-\Gamma\cdot r) = \exp(-H/c_0\cdot r) \hieruit \boxed{\large \Gamma = \frac{H}{c_0}} $$ Pierre-Simon's constant can be calculated now. 

# 1 megaParsec
Mpc := 3.08567758*10^22;
# Hubble parameter (2022-02-08)
H := 73.4*1000/Mpc;
# Speed of light
c_0 := 299792458;
# Gamma
H/c_0;
                                         -26
                          0.7934595873 10
It turns out to be very small indeed, approximately $\,8 \times 10^{-27}\, m^{-1}$. By the way, this is $\approx$ twice the value as found by Amitabha Ghosh at page 47 in his book Origin of Inertia.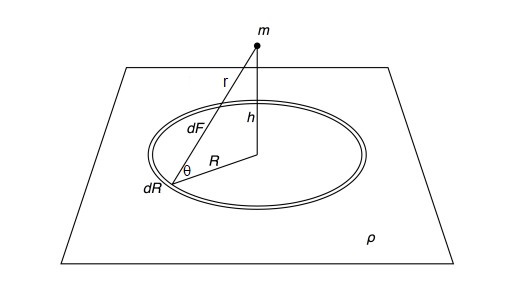
It should be noticed that Laplace's modification of the law of gravitation is quite in concordance with UAC theory. Take a look at A Basic Equation and put $\,\vec{v}_t=0\,$ in there: $$ e^{-H/c_0\,\cdot\, r}\;\vec{a}_T = \vec{a}_t - \half H\,\vec{v}_t \hieruit m_0\,\vec{a}_t = e^{-\Gamma r}\;m_0\,\vec{a}_T = G\frac{m_0\,d\mu_0}{r^2}\,e^{-\Gamma r} $$ where $\,r\,$ is the distance between our test mass $\,m\,$ and the infinitesimal cosmic mass $\,d\mu\,$.

Seeliger's Gravitational Paradox and the Infinite Universe

There are a few typos - read: errors - in this paper by Leonardo Sarasúa, which is a good reason to revisit the maths.

Of course there does not exist an thickness zero for the ring in the above picture; it must be $\,dh\,$ instead. Giving a slightly but essentially different expression for the infinitesimal (vertical) force on the particle with mass $\,m\,$. $$ dF = \frac{G\,m(\rho\,2\pi R\,dR\,dh)}{\left(\sqrt{R^2+h^2}\right)^2}\frac{h}{\sqrt{R^2+h^2}} = 2\pi G m \rho\,h\,dh\frac{R\,dR}{(R^2+h^2)^{3/2}} $$ The total force experienced by the test mass from all of the mass below it is $$ F = 2\pi G m \rho \int_0^{\infty} h \left[ \int_0^{\infty} \frac{R\,dR}{(R^2+h^2)^{3/2}}\right] dh $$ The integral between square brackets is, with $\,x=R/h\,$ and $\,u=x^2+1\,$: $$ \int_0^{\infty} \frac{R\,dR}{(R^2+h^2)^{3/2}} = \frac{h^2}{h^3} \frac{1}{2} \int_{x=0}^{\infty} \frac{d(x^2+1)}{(x^2+1)^{3/2}} = \frac{1}{h} \frac{1}{2} (-2) \left[-\frac{1}{\sqrt{u}}\right]_1^\infty = -\frac{1}{h} $$ Giving for the total force experienced by our test mass an infinite outcome. $$ F = - 2\pi G m \rho \int_0^{\infty} dh = - \infty $$ Minus another minus infinite outcome if the mass of the universe at the other side (above it) is taken into account. Therefore the total force is undefined. This comprises the paradox.
However, let's now introduce the panacea as proposed by Laplace and Seeliger and observe what happens. $$ F = 2\pi G m \rho \int_{-\infty}^{+\infty} h \left[ \int_0^{\infty} \frac{e^{-\Gamma\sqrt{R^2+h^2}}R\,dR}{(R^2+h^2)^{3/2}}\right] dh $$ With :-(brainless)-: help of MAPLE 8 we see that the outcome is zero again, as desired and required. Physical truth should not depend upon the way you look at it. 
h*int(R*exp(-Gamma*sqrt(R^2+h^2))/(R^2+h^2)^(3/2),R=0..infinity);
f(h) := simplify(%,assume=positive);
int(f(h),h=-infinity..infinity);
                                      0
Come on! It must be possible again to do this with Brain on, computer off ! Define $\,I\,$ as half the above integral: $$ I = \int_0^{\infty} h \left[ \int_0^{\infty} \frac{e^{-\Gamma\sqrt{R^2+h^2}}R\,dR}{(R^2+h^2)^{3/2}}\right] dh \\ u = \sqrt{R^2+h^2} \SP v = \frac{h}{\sqrt{R^2+h^2}} \SP h = uv \SP du\,dv = \frac{\partial(u,v)}{\partial(R,h)}dR\,dh = \left| J \right| dR\,dh $$ From the picture we see that $\,u=r\,$ and $\,v=\sin(\theta)\,$, giving the integration bounds $\,0\le u \lt\infty\,$ and $\,0\le v \le 1\,$. $$ \left| J \right| = \begin{vmatrix} \partial u/\partial R & \partial u/\partial h \\ \partial v/\partial R & \partial v/\partial h \end{vmatrix} = \begin{vmatrix} R/\sqrt{R^2+h^2} & h/\sqrt{R^2+h^2} \\ -Rh/(R^2+h^2)^{3/2} & 1/\sqrt{R^2+h^2} - h^2/(R^2+h^2)^{3/2} \end{vmatrix} = \frac{R}{R^2+h^2} \\ u^2 = R^2+h^2 \hieruit R^2 = u^2-h^2 = u^2(1-v^2) \hieruit R = u\sqrt{1-v^2} \hieruit \left| J\right| = \frac{\sqrt{1-v^2}}{u} \\ I = \iint uv \cdot \frac{e^{-\Gamma\,u}\,u\sqrt{1-v^2}}{u^3} \left(\frac{u}{\sqrt{1-v^2}}\right)du\,dv = \int_0^\infty e^{-\Gamma\,u}\,du \cdot \int_0^1 v\,dv = \frac{1}{2\Gamma} $$ If the force components on the test particle from below and from above are considered separately, then we observe that each of the corresponding integrals is equal to the same (extremely large) value. So these finite outcomes neatly cancel each other out. Formally, with $\,g=-h\,$: $$ F = 2\pi G m \rho \left\{ \int_{-\infty}^{0} h \left[ \int_0^{\infty} \frac{e^{-\Gamma\sqrt{R^2+h^2}}R\,dR}{(R^2+h^2)^{3/2}}\right] dh + \int_{0}^{\infty} h \left[ \int_0^{\infty} \frac{e^{-\Gamma\sqrt{R^2+h^2}}R\,dR}{(R^2+h^2)^{3/2}}\right] dh \right\} \\ F = 2\pi G m \rho \left\{ - \int_0^\infty g \left[ \int_0^{\infty} \frac{e^{-\Gamma\sqrt{R^2+g^2}}R\,dR}{(R^2+g^2)^{3/2}}\right] dg + \int_{0}^{\infty} h \left[ \int_0^{\infty} \frac{e^{-\Gamma\sqrt{R^2+h^2}}R\,dR}{(R^2+h^2)^{3/2}}\right] dh \right\} \\ F = 2\pi G m \rho \left\{ - \frac{1}{2\Gamma} + \frac{1}{2\Gamma} \right\} = 0 $$ The physical meaning of $\,1/\Gamma=c_0/H\,$ is the speed of light times a Hubble time. Which in some circles is called the size of the (observable) universe. Thus what we finally have is the force exerted on the test particle by half the universe below it, canceled by the force of half the universe above it. So to speak. Whatever. Whether the so-called Observable universe has a radius or not, it anyway has sort of a decay distance $\,1/\Gamma\,$ in the exponential function $\,\exp(-\Gamma\,r)\,$. And this (not expanding / not comoving) characteristic very much Euclidean distance is calculated to be 
# Seconds in a year
year := 31556926;
# 1/Gamma
c_0/H/(c_0*year)/10^9;

                             13.32170443 # 13 billion light years