Louis Marmet via A Cosmology Group
[ di 15 nov. 21:32 ] rewrite Amitabha's equation for F2 by substituting y => -y (as someone did that on math.stackexchange). This gives the equations in the image below.
The physical interpretation of these equations is:
(1 + x^2 + 2xy) = r^2 is the square of the radius from a test mass P.
(xy+1)/r is the fraction of the force component toward the center of a sphere.
x^2 dx is the mass of a spherical shell element of radius x.
F1, the integral over x from 0 to 1, gives the force exerted by a filled sphere of radius = 1 on a test mass P located on the surface of the sphere. A positive value means the force points toward the centre of the sphere.
F2, the integral over x from 1 to infinity, gives the force exerted by matter outside the sphere of radius = 1 on the test mass P. (Think of one hole in an infinite Swiss cheese.) A positive value means that the force points away from the centre of the spherical hole.
Therefore, F1 - F2 is the total force on point P exerted by uniform cheese everywhere from 0 to infinity. Since for each mass element on one side of P there is another mass element at the same distance on the other side and the integral converges for alpha>0, the total force on P is cancelled and F1 - F2 = 0.
Those hard to solve equations are just a mathematical formulation of a simple physical problem that has lost its symmetry because the coordinate system has been translated to the edge of an arbitrary sphere. The physics remains the same and the null solution is trivial, without the need of numerical estimates or MAPLE. It is not so interesting that the exponential exp(-alpha r) makes the integral F2 converge for alpha>0. There is no infinite Swiss cheese, so all integrals of this type, that have any physical significance, converge.
As for the "paradox" that never really existed (c.f. Pierre), it has disappeared.
[ Nov 23 at 23:23 ] Define
$$ F(\alpha) = \int_0^\infty\int_0^\pi {\rm e}^{-\alpha r} \sin \theta \, \cos \theta \, {\rm d}\theta \, {\rm d}r $$
Integrating yields
$$ F(\alpha) = -\frac{1}{\alpha} \left. {\rm e}^{-\alpha r} \right|_{r=0}^\infty
\;\cdot\; \left. \frac{1}{2} \sin^2 \theta\,\right|_{\theta=0}^\pi = 0
\quad \text{for all } \alpha>0, $$ but does not exist for $\alpha = 0$.
Map the function using $u = -r \cos \theta$, $v = r \sin \theta$ and the determinant of the Jacobian
$$ \left| J \right| = \left|
\begin{matrix}
\frac{\partial u}{\partial \theta} = r \sin \theta & \frac{\partial u}{\partial r} = -\cos \theta \\
\frac{\partial v}{\partial \theta} = r \cos \theta & \frac{\partial v}{\partial r} = \sin \theta
\end{matrix} \right| = r$$
This gives
$$ F(\alpha) =
\int_0^\infty \int_0^\pi \frac{{\rm e}^{-\alpha r} \sin\theta \cos\theta}{r} \, r \, {\rm d}\theta \, {\rm d}r =
\int_0^\infty \int_{-\infty}^\infty \frac{{\rm e}^{-\alpha \sqrt{u^2 +v^2}} uv}{(u^2 +v^2)^{3/2}} \, {\rm d}u \, {\rm d}v
$$
The integration limits are determined from this map:
map from r, $\theta$ to u, v
The origin is shifted by one, $u \rightarrow u +1$, to give
$$ F(\alpha) =
\int_0^\infty \int_{-\infty}^\infty \frac{{\rm e}^{-\alpha \sqrt{u^2 +2u +1 +v^2}} (u +1)v}{(u^2 +2u +1 +v^2)^{3/2}} \, {\rm d}u \, {\rm d}v
$$
Map again using $y = -\cos\theta' = u/\sqrt{u^2 +v^2}$, $x = r' = \sqrt{u^2 +v^2}$, $u = xy$ and the determinant of the Jacobian
$$ \left| J \right| = \left|
\begin{matrix}
\frac{\partial y}{\partial u} = 1/x -u^2/x^3 & \frac{\partial y}{\partial v} = -uv/x^3 \\
\frac{\partial x}{\partial u} = u/x & \frac{\partial x}{\partial v} = v/x
\end{matrix} \right| = v/x^2$$
$$ F(\alpha) =
\int_0^\infty \int_{-\infty}^\infty \frac{x^2}{v} \frac{{\rm e}^{-\alpha \sqrt{u^2 +2u +1 +v^2}} (u +1)v}{(u^2 +2u +1 +v^2)^{3/2}} \, \frac{v}{x^2} \, {\rm d}u \, {\rm d}v $$
$$ = \int_0^\infty x^2 \int_{-1}^1 \frac{{\rm e}^{-\alpha \sqrt{x^2 +2xy +1}} (xy +1)}{(x^2 +2xy +1)^{3/2}} \, {\rm d}y \, {\rm d}x
$$
$x$ acts as a radius, $y$ is the fraction of $x$ along $u$. The integration limits are determined from this map:
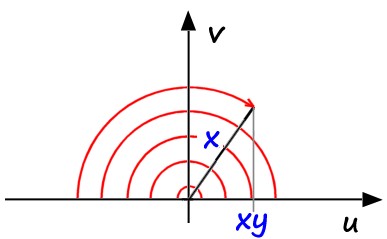map from u, v to x, y
So we have
$$ F(\alpha) = \int_0^{\infty} x^2 \int_{-1}^1 \frac{{\rm e}^{-\alpha \sqrt{1 +x^2 +2xy}} (xy +1)} {(1 +x^2 +2xy)^{3/2}} \, {\rm d}y \, {\rm d}x = 0 \quad \text{for all } \alpha>0, $$ but not for $\alpha = 0$.