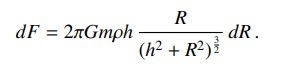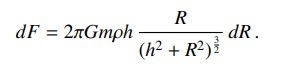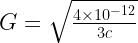Latest revision 15-06-2025
Seeliger's Paradox
Finding errors
It might raise more enthusiasm for the subject if we demonstrate how to pinpoint errors in a paper without understanding much of the math.
As an example, let's take
Seeliger's Gravitational Paradox and the Infinite Universe.
On page 166 of this (published & accepted) paper the following formula is observed.
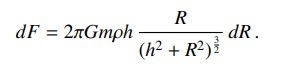The first thing we have to know in order to establish the correctness of a formula is what the physical dimensions are.
Here goes again for the example at hand.
$dF=$ force. The unit of force is the Newton (Wikipedia) which is ($kg\,m/s^2$), giving $[dF] = mass\times length/time^2$ .
$2\pi$ is a pure math number; there is nothing physical with that: $[2\pi] = 1$ .
$G=$ gravitational constant. Google it up, then you will see that its unit ($m^3/kg/s^2$) ,
hence is physical dimension is: $[G] = length^3/mass/time^2$.
$m=$ mass, $\rho=$ density, which is mass divided by volume, so $[m] = mass$ , $[\rho] = mass/length^3$ .
$[R,h,dR] = length$ , $[(h^2 + R^2)^{3/2}] = length^3$ .
Now we have all of the ingredients for simplifying the formula at hand into one with physical dimensions only.
$$ [dF] = \frac{[2\pi][G][m][\rho][h][R][dR]}{(h^2 + R^2)^{3/2}} \\
mass\times length/time^2 =
(length^3/mass/time^2)\times mass\times (mass/length^3)\times length\times length\times length / length^3 = mass/time^2
$$
It follows that a dimension of length is missing at the right hand side, when simplified to length = 1 , which is not true.
Matching of physical dimensions, however, is a necessary condition. It is a Sine qua non.
Therefore, whatever theory is built on the formula as displayed cannot be alright.
But it is important to remember that such proper matching is only a necessary condition.
It certainly is not sufficient (as e.g. Bud Rapanault will be happy to confirm).
For the sake of completeness, here is the correct formula. An infinitesimal length $dh$ has been missing.
$$
dF = 2\pi G m \rho h\,{\bf dh}\,\frac{R}{(R^2+h^2)^{3/2}}dR
$$
By now the treatment of Seeliger's Paradox section at my website can be sucessfully completed.
Another example. At the website by Bud Rapanault,
named This Island Universe,
we find another remarkable, lonesome, formula.
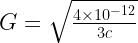
Obligatory check on physical dimensions again: $[G] = length^3/mass/time^2$ , $[c] = length/time$ .
It is easily seen that the dimensions at the left do not match with those on the right:
$$
(length^3/mass/time^2)^2 \ne (length/time)^{-1}
$$