Latest revision 15-06-2025
index
Dimensions check
At the website by Sahil Gupta, named The Big Circus Model , we find this remarkable formula.
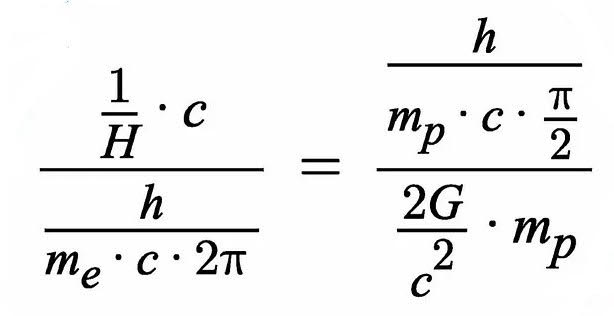
Google up, if knowledge has become rusty:
Gravitational constant $G$ ,
Speed of light $c$ ,
Planck's constant $h$ ,
Hubble constant $H$ ,
Proton mass $m_p$ ,
Electron mass $m_e$ .
The first thing I always do, when encountering a formula like this, is a check on physical dimensions.
Here goes: $[G]=length^3/mass/time^2$ , $[c]=length/time$ , $[h]=length^2\times mass/time$ , $[H]=time^{-1}$ , $[m_p]=[m_e]=mass$ .
Now treat the physical dimensions as if they were common variables. And simplify.
$$
(time\times length/time) / ((length^2\times mass/time)/(mass\times length/time)) = \\
((length^2\times mass/time)/(mass\times length/time)) / ((length^3/mass/time^2)/((length/time)^2)\times mass) \\
(time\times length/time) / ((length^2\times mass/time)/(mass\times length/time))) = 1 \\
((length^2\times mass/time)/(mass\times length/time)) / ((length^3/mass/time^2)/((length/time)^2)\times mass) = 1
$$
Thus two dimensionless numbers to compare: 1 = 1. It cannot be better.
Upon substituting real world values Sahil proves that the left hand side divided by the right hand side is approximately unity.
Meaning that two physically "independent" large numbers have the same order of magnitude. Coincidence or not?
The advantage of a Computer Algebra System is that it can handle variables without a numerical value with the same ease.
Independent confirmation follows (with MAPLE).
c := 299792458 * length/time; # Speed of light
Mpc := 3.08567758*10^22; # Megaparsec
H := 70*1000/Mpc * 1/time; # Hubble tension
G := 6.67408*10^(-11) * length^3/mass/time^2; # Gravitational constant
m_e := 9.1093837015*10^(-31) * mass; # Electron mass
m_p := 1.67262192*10^(-27) * mass; # Proton mass
h := 6.62607015*10^(-34) * length^2*mass/time; # Planck constant
left := evalf((c/H)/(h/(m_e*c*2*Pi)));
right := evalf((h/(m_p*c*Pi/2))/(2*G/c^2*m_p));
quotient := evalf(left/right);
39
left := 0.3422210705 10
39
right := 0.3386412696 10
quotient := 1.010571071
Core reference is a paper by Patrick G. Tonin entitled
The Quantum Bang Hypothesis:
An Alternative to Dark Matter and Dark Energy.
We start at section 2 of the paper. There the author says: We hypothesize that the quantum realm and the cosmos
are linked by a scale relation.
It is the first thing, actually the only thing we are going to investigate here.
It has been argued in my ACG e-mail posts that the paper is at least mathematically correct.
So attention can be restricted to physics only.
The scale relation, according to the author, is supposed to be defined as follows.
$\alpha_G$ is the gravitational coupling constant defined using a pair of protons ($\alpha_G = (m_{pr}/m_p)^2$).
That definition didn't make sense to me at first sight.
Later on the author explained in an e-mail what the meaning is of the symbols.
The main cause of the confusion is that our own notation is a bit different: $m_{pr}\to m_p =$ proton mass, $m_p \to m_P=$
Planck mass $=\sqrt{\hbar c/G}$.
Is that a pair of protons? I think not. Whatever. After having resolved my misunderstanding the algebra is simple:
$$
\alpha_G = \left(\frac{m_p}{m_P}\right)^2 = \frac{m_p^2}{(\sqrt{\hbar c/G})^2} = \frac{G\,m_p^2}{\hbar c}
$$
But meanwhile I had started a reverse engineering procedure in order to find a more satisfactory definition.
And this is what I found, for a real pair of protons placed at a distance $\,r\,$ from each other.
$\alpha_G=$ (Newton's law)
/ (Coulomb's law)
$\times$ (Fine-structure constant)
$$
\alpha_G = \Large \frac{\frac{G\,m_p\,m_p}{r^2}}{\frac{e\,e}{4\pi\varepsilon_0\,r^2}} \normalsize \times \alpha
\quad \mbox{with} \quad \alpha = \frac{e^2}{4\pi\varepsilon_0 \hbar c} \\ \mbox{Simplified:} \quad \alpha_G = \frac{G\,m_p^2}{\hbar c}
$$
Here: $G=$ gravitational constant, $m_p=$ proton mass, $\hbar=$ reduced Planck constant, $c=$ lightspeed.
The result ${\bf \alpha_G}$ is a dimensionless constant, namely (force / force) x $\alpha$ : it is a pure number.
Then the paper says: We propose the following three novel equations from which our cosmological model is deduced.
Three equations. Let's check if there is numerical agreement between Patrick's findings and ours.
A computer algebra system (MAPLE) is employed, thus avoiding errors.
c := 299792458; # Speed of light
G := 6.67408*10^(-11); # Gravitational constant
m_e := 9.1093837015*10^(-31); # Electron mass
m_p := 1.67262192*10^(-27); # Proton mass
h := 6.62607015*10^(-34); # Planck constant
h_bar := h/(2*Pi); # Reduced Planck constant
alpha_G := evalf(G*m_p^2/(h_bar*c)); # The coupling constant
lambda_e := h/(m_e*c); # Electron Compton length
t_e := h/(m_e*c^2); # Electron Compton time
t_0 := evalf(t_e/(Pi*alpha_G)); # First formula
year := 31556926; evalf(t_0/year/10^9);
R_h := c*t_0; # Second formula
mu := m_p/m_e;
M_u := mu^2*m_e/alpha_G^2; # Third formula
M_u := evalf(R_h*c^2/(2*G)); # The same
Mpc := 3.08567758*10^22; # Megaparsec
H_0 := 1/t_0 * Mpc/1000;
.......................................
-38
alpha_G := 0.5905954709 10
.......................................
H_0 := 70.73997502 # km/s/Mpc
The universe as proposed by the author has the critical
Schwarzschild radius:
$$
R_h = \frac{2GM_u}{c^2}
$$
All of our own results are in agreement with those by Patrick. And because of $\,R_h := c t_0\,$ and $\,M_u = R_h c^2/(2 G)\,$
we only have to check the first one: $t_0 = 4.361999816\times 10^{17}\;s$ , which is OK.
Worth noticing is Tonin's value for the Hubble constant $\,H_0\,$.
This value falls between the Planck Collaboration 2018 estimate [4] of $H_0 = 67.37 \pm 0.54\; km\,s^{-1}Mpc^{-1}$
and the distance-ladder estimate from the SH0ES project 2019 [5] of $H_0 = 74.03 \pm 1.42 \; km\,s^{-1}Mpc^{-1}$.
Another consequence is a well known formula involving the mean mass density $\,\rho_u\,$ of the universe (whatever that is supposed to mean):
$$
R_h = \frac{2GM_u}{c^2} = \frac{2G}{c^2} \rho_u \frac{4}{3}\pi R_h^3 \\
1 = \frac{2G}{c^2}\rho_u \frac{4}{3}\pi\left(\frac{c}{H_0}\right)^2 \quad ; \quad H_0^2 = \frac{8}{3}\pi\,G\,\rho_u \\
\boxed{ H_0 = \sqrt{\chi\,G\,\rho_u} \quad \mbox{with} \quad \chi = \frac{8}{3}\pi \quad (: \Lambda\mbox{CDM}) }
$$
The advantage of the doubt is on hold at section 5, where the author writes: In order for Equation (1) to be valid as
the Universe ages, either the gravitational coupling constant $\alpha_G$ or the electron Compton time $t_e$, or both, have to vary.
Indeed Equation (1) and later on Equation (4) represents a problem, provided that the quantities involved are all true constants of nature.
If $t_0$ is the age of the universe given by Equation (1), then that age cannot become larger now as time proceeds. Which is indeed absurd.
However, a remedy by making quantities varying with time, as proposed by Patrick, is that going to work? According to the paper we have:
$$
\alpha_G(t) \sim t^{-2} \quad (9)\; ; \quad m_e(t) \sim t^{-2} \quad (16)\; ; \quad G(t) \sim t^{-1} \quad (18)\; ; \quad h(t) \sim t^{-3} \quad (19)
$$
Prediction 4: The mass and size of particles decrease with cosmic time.
So likewise: $m_p(t) \sim t^{-2}$. It follows that (9) is OK:
$$
\alpha_G = \frac{G\,m_p^2}{\hbar c} \sim \frac{t^{-1}t^{-2}t^{-2}}{t^{-3}} = t^{-2}
$$
But how about the Fine-structure constant.
$$
\alpha(t) = \frac{e^2}{4\pi\varepsilon_0 \hbar c} \sim t^{-3}
$$
This seems to be contradictory to experience;
empirical evidence has revealed that the fine structure constant is the same everywhere in the universe and does not vary.
But I'm not sure, because nothing has been said about the time dependence of electrical and thermodynamical quantities.
It's interesting to make a comparison between $\alpha_G$ and the right hand side of the formula by Sahil Gupta.
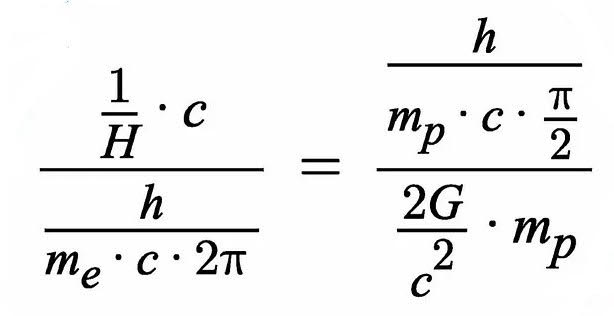 The inverse of the latter can can be simplified to:
$$
\frac{2G}{c^2}.m_p \times \frac{m_p.c.\pi/2}{h} = \frac{1}{2}\frac{G\,m_p^2}{\hbar\,c} = \alpha_G/2
$$
Numerical confirmation:
The inverse of the latter can can be simplified to:
$$
\frac{2G}{c^2}.m_p \times \frac{m_p.c.\pi/2}{h} = \frac{1}{2}\frac{G\,m_p^2}{\hbar\,c} = \alpha_G/2
$$
Numerical confirmation:
right := evalf((h/(m_p*c*Pi/2))/(2*G/c^2*m_p));
alpha_G := 2/right;
-38
alpha_G := 0.5905954709 10
How about Sahil's left hand side? Referring to the paper by Patrick G. Tonin we find with equation (4) for the inverse of that number:
$$
H_0 = \frac{c}{R_h} = \frac{\pi \alpha_G}{t_e} \quad \mbox{with} \quad t_e = \frac{h}{m_e c^2} \\
\frac{h}{m_e.c.2\pi} \times \frac{H}{c} = \frac{h}{m_e c^2}\frac{1}{2\pi} \times \frac{\pi \alpha_G}{t_e} = \alpha_G/2
$$
Conclusion: From The Quantum Bang Hypothesis by Patrick G. Tonin it follows that,
in the formula by Sahil Gupta, left hand side and right hand side are exactly equal:
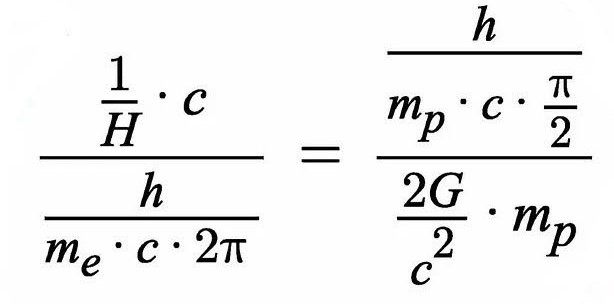 $= 2/\alpha_G$
$$ \boxed{\frac{1}{\mbox{left}} = \frac{1}{\mbox{right}} \; \mbox{(Gupta)} = \frac{\alpha_G}{2} \; \mbox{(Tonin)}} $$
$= 2/\alpha_G$
$$ \boxed{\frac{1}{\mbox{left}} = \frac{1}{\mbox{right}} \; \mbox{(Gupta)} = \frac{\alpha_G}{2} \; \mbox{(Tonin)}} $$
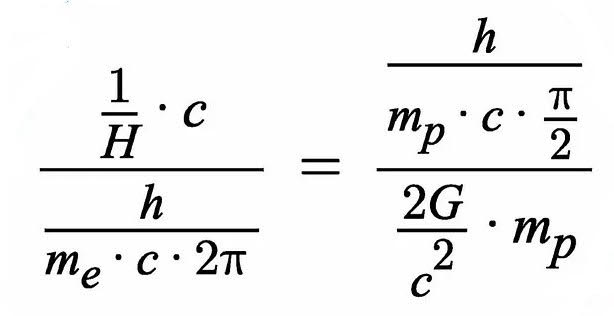
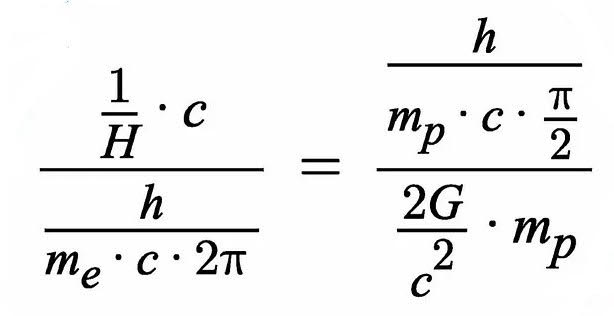
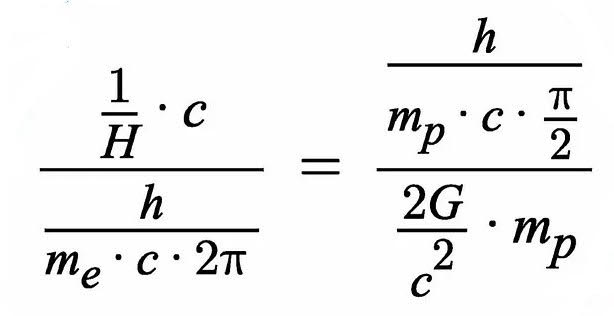
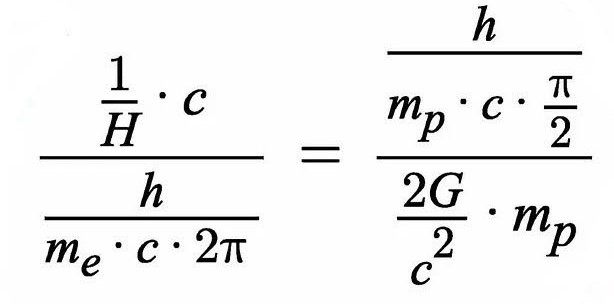 $= 2/\alpha_G$
$= 2/\alpha_G$