This web page is mainly about Complex Analysis. If you feel - like I do - like walking on thin ice with the subject, then you should start with checking out some undergraduate stuff in the first place, because our key reference is a book at the beginning (?) graduate level:

[ CMS ] "Complex Made Simple", by David C. Ullrich

The author is a well known personality in the 'sci.math' newsgroup.
There are captions like Abstract, Summary, Overview in certain books, but not in this one. Though it seems that such captions have been invented for a purpose ..
Other criticism concerns the somewhat chaotic subdivision in chapters, which sometimes seem to serve no other purpose than to keep the labels of the mathematical statements smaller than would be the case with a continuous story, and no chapters at all. All of this concerns the form, not the content. (And much of it is a matter of personal taste)

Complex Made Simple: Update

CMS: Complex Made Simpler

It's an attempt to make Complex Analysis even more comprehensible, among other things by putting somewhat more emphasis on computation and visualisation, while appreciating Ullrich's work as a theoretical foundation. So it's meant as sort of supplementary (and hopefully complementary too) College Notes.

Chapter 0. Differentiability and the Cauchy-Riemann Equations

Published in 'sci.math':

Complex Heuristics
Careful reading instead of skimming through CMS certainly could have prevented some of my postings in this thread, though it has produced some interesting side effects (: commuting matrices).

Bad complex functions
Absorbing some more undergraduate stuff could have prevented this posting as a whole, because these "bad complex functions" can be detected by checking out if the Cauchy-Riemann equations are valid for their real and imaginary parts. If such is not the case, then they are not holomorphic, which is a neater way to express the "bad" name calling.
Back to work:
Chapter 1. Power Series
Proof (Proposition 1.1) on page 12. Instead of having that function F(z,w) dropped out of the blue sky, let it be explained in excruciating detail:
```
Lemma: Sum(k=0,k=n-1) z^k.w^(n-k-1) = (z^n - w^n)/(z - w)  for z <> w
Proof.
  Let:  f_n(z,w) = Sum(k=0,k=n-1) z^k.w^(n-k-1)
      z.f_n(z,w) = Sum(k=0,k=n-1) z^(k+1).w^(n-k-1)
                 =       z.w^(n-1) + z^2.w^(n-2) + .. + z^(n-1).w + z^n
      w.f_n(z,w) = Sum(k=0,k=n-1) z^k.w^(n-k)
                 = w^n + z.w^(n-1) + z^2.w^(n-2) + .. + z^(n-1).w
----------------------------------------------------------------------
(z - w).f_n(z,w) = - w^n                                          + z^n

Lemma: Sum(k=0,k=n-1) z^k.z^(n-k-1) = f_n(z,z) = n.z^(n-1)  for z = w 

Define:   F(z,w) = Sum(n=0,n=oo) c_n . f_n(z,w)
```
Published in 'sci.math':
- CMS: Smoothed Complex Series
Theorem (HdB). Any Smoothed Complex Series is an Entire Function.
The meaning of this theorem is, in the first place, that we can effectively get rid of any radius of convergence. A smoothed complex series just converges everywhere. It also means that we can construct a complex series with random, but smoothed, coefficients and any such a series then converges everywhere as well. Random complex series with smoothed coefficients appear as smoothed but random closed curves, when restricted to arguments on the unit circle. That is because Complex Analysis is, in some sense: Fourier Analysis in disguise. See Fuzzyfied Lissajous Analysis for details.
Chapter 2. Preliminary Results on Holomorphic Functions
Published in 'sci.math':
- CMS: arbitrary too simple closed curves and the like with self-intersection (easier) ,
  with accompanying theory , executables & source , postings [ 1 ] , [ 2 ] in sci.math .
- CMS: Cauchy's theorem applied correctly ?
- CMS: arbitrary too simple closed curves
Excercise 2.1 on page 16 shows that Complex Analysis is in some sense more real(istic) than Real Analysis. Because a function which is feeling "bad" in a physical sense, like f(z) = z^2.sin(1/z) , is indeed complex singular at z = 0, but not real singular at x = Re(z) = 0 .
Lemma 2.1. (ML Inequality) on page 18: L is the length of γ . But this can only be the case if γ is not, for example, a Space-filling curve, with "infinite" length L . Curves called rectifiable are mentioned, but not explained, in the book on page 16.
Example on page 20 shows that ∫_γ dz / z = 2π.i where γ : [0,2π] => C is γ(t) = r.e^i.t with real r > 0 .
Nice place to hook in and show that, with the same closed curve (being a circle with radius r) :
∫_γ z^m dz = 0 or 2π.i and the latter only for m = -1 , where m is an integer. Enhance and repeat:

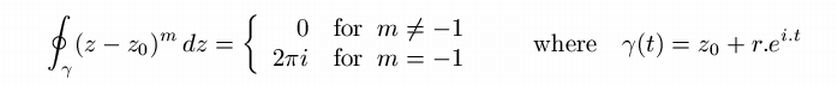
So, indeed it is in some sense hust about the only way to get something nonzero by integrating an analytic function with an "isolated singularity" over a closed curve.
On the same page, it reads: we have not given a definition of what it means for a point to lie "inside" a closed curve. In fact we will not be giving any such definition. Everybody seems to be affraid of the Jordan curve theorem. As a consequence of the paranoia, concepts which are intuitively clear - like "inside / outside" - are rather dismissed as "undefined". Irritating in the first place. And not quite neccessary as well. It makes content of CMS more difficult to absorb. And it distracts attention from issues more relevant than this.
Worse. Spending so much effort on the generality of (closed) curves needed to evaluate the complex line integrals, it sounds like a worthwile undertaking, but it isn't. The reason is the following. A theory called Lissajous Analysis shows that any closed smooth curve can be represented by a Fourier Series, which is the same as a Complex Laurent Series specified for the unit circle. The reverse is also true. Any complex Laurent series, when specified for the unit circle, represents a closed smooth curve. Actually it means that a line integral over an arbitrary smooth closed curve can always be converted into a line integral over the unit circle:
∫_γ f(z) dz = ∫_O f(γ(z)) γ'(z) dz
An argument remotely similar to the above is found in CMS on page 80 as Theorem 5.1 (The Argument Principle). Oh well, not even remotely, it seems ..
So what are we interested in? More complicated contours or complicated complex functions? I wouldn't vote for the extreme and ONLY admit integrations over the unit circle. But the above shows that a constraint to, say, simple closed curves is very much reasonable. And that the reverse strategy - complicated contours - impressive as it may seem, is in fact rather futile: a parametrization issue.
Mathematics can be too general for comfort. If the generalization of a special result is more or less trivial, then show some restraint and go for the specialization.
Example. Let γ(z) = zⁿ with n ∈ N , then γ is prototype of a curve winding around itself (winding number =) n times and:
∫_γ dz / z = ∫_O n z^n-1 / zⁿ dz = n ∫_O dz / z = n 2 π i
Theorem 2.2 (Cauchy-Goursat: Cauchy's Theorem for triangles). Ullrich's Proof on page 23 starts with "Suppose not." : thereby suggesting a proof by contradiction. But only suggesting. The proof is actually a straightforward one, i.e. a direct proof.
It is noted that the (quite ingenious) proof of Cauchy-Goursat uses the fact that the absolute value of the complex derivative is maximal somewhere inside the triangles. Such is for example not the case with the function f(z) = 1/z . Thus the theorem need not to be valid for such a function (actually it isn't). The reverse is not true. If a function is singular, then the integral around the singularity can (easily) be zero.
Example. f(z) = 1/z² => ∫_|z|=1 dz / z² = 0 .
On page 23 it also reads that you can get the conclusion from Green's theorem , i.e. for complex (thus real) differentiable functions within simply closed (Jordan) curves:
- Cauchy Integral Theorem
Also read Ullrich's comment on this treatment.
Note. The Least Squares Finite Element Method for Ideal Flow can be interpreted as the Cauchy Integral Theorem applied to Numerical Analysis. Take a look at page 6 of the article when seeking for confirmation of this fact (Green's Theorem being the would-be real valued equivalent of Cauchy's).
Chapter 3. Elementary Results on Holomorphic Functions
analytic functions are locally nothing more than glorified polynomials.
Published in 'sci.math':
- CMS: where are the zeroes?
  With pictures [ 1 ] , [ 2 ] , [ 3 ] , [ 4 ] , [ 5 ] , [ 6 ] , [ 7 ] ,
  while investigating the initial polynomial 1 + z + z² / 2! + z³ / 3! + z⁴ / 4! ... + zⁿ / n! of the entier function e^z ,
  with help of Rouché's Theorem (I love this Wikipedia source. Because now it has become my theorem as well)
A Complex Newton-Rhapson method is employed in the software.
Note. The fact that |e^z| → 0 for |z| → ∞ and Re(z) < 0 explains why much of the region on the left is close to zero (: black) in the visualization.
Corollary 3.7 (Fundamental Theorem of Algebra) on page 37. Quote: for us it's just an amusing digression, at least for now. Back to work. The following formula, expressing any complex polynomial in its roots, is even between scaring parentheses: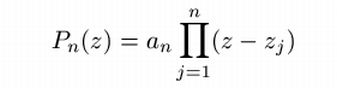

Why oh why, this seemingly disdainful treatment of a most impressive result? Has the author forgotten that this is the main thing Complex Analysis has been invented for in the old days? A preliminary version of The Argument Principle can be derived at this place. It's almost as if we have jumped into
Chapter 5. Counting Zeroes and the Open Mapping Theorem , with:
- Counting Zeroes of Polynomials
Example. The other way around. Let P(z) = 2 + z² . Let O(t) = R.e^{i t} . Then 1/(2 π i) ∫_O P'(z) / P(z) dz = 1/(2 π i) ∫_P dz / z where P(t) = 2 + R².e^{2 i t} .
If we choose for example R = 1.5 , then the pole is inside the curve P(t) and because the winding number is 2 , the outcome of the integral = 2 = number of zeroes.
This line of thought seems to be remotely similar to the Sketch of a Proof by Birkhoff and MacLane. Other favorites are easily found at this website.
Theorem (remotely resemblant to the Picard theorems). A polynomial of degree n assumes all complex values c exactly n times.
Proof. a_n zⁿ + a_n-1 z^n-1 + ... + a₂ z² + a₁ z + a₀ - c = 0 has n zeroes.
A reasoning as in the last paragraph on page 40 of CMS could also be employed for other "Special Functions" than f(z) = exp(c.z) : f(z) = c.z ; f(z) = c.ln(z) ; f(z) = z^c .
Chapter 4. Logarithms, Winding Numbers and Cauchy's Theorem
- Methods of contour integration
- Residue (complex analysis)
Chapter 5. Counting Zeroes and the Open Mapping Theorem
On page 80 of CMS we find Theorem 5.1 (The Argument Principle). On the Internet (Wikipedia), however, the Argument principle is not only about zeroes, but about zeroes and poles. An advantage of the latter is that it's easier to prove (the traditional version of) Rouché's Theorem. Insofar as the Proof of Lemma 5.2. on page 81 is concerned, a picture says more than a thousand words:

And a thousand words are needed indeed, if people are driven paranoia due to inside / outside issues.
Theorem 5.4 (Rouché's Theorem). Suppose that γ is a smooth closed curve in the open set V such that Ind(γ,z) is either 0 or 1 for all z ∈ C \ γ^* and equals 0 for all z ∈ C \ V , and let Ω = { z ∈ V : Ind(γ,z) = 1 } . If f , g ∈ H(V) and | f(z) - g(z) | < | f(z) | + | g(z) | for all z ∈ γ^* then f and g have the same number of zeroes in Ω .
Also sprach David C. Ullrich. This author would rather say: let γ, V, Ω, z be as in the picture below and ..

Open mapping theorem (complex analysis)
Chapter 6. Euler's Formula for sin(x)
An overly complicated treatment that can easily be replaced by a page or two:
- Euler-Wallis formula for sin(x) (HdB)
- and a picture of f(x) = x/tan(x)
Research for the above via 'sci.math':
- CMS: Euler's Formula for sin(x)
Later:
- Weierstrass factorization theorem
Chapter 10. Harmonic Functions
10.6. Intermission: Harmonic Functions and Brownian Motion, page 200
This rather Off-Topic one as a result from skimming, not reading:
- Surely You're Joking, Mr. Ullrich !
Chapter 22. More on Brownian Motion
- Question about "Complex Made Simple"
Off Topic

CMS: Complex Made Simpler

Chapter 0. Differentiability and the Cauchy-Riemann Equations

Chapter 1. Power Series

Chapter 2. Preliminary Results on Holomorphic Functions

Chapter 3. Elementary Results on Holomorphic Functions

Chapter 4. Logarithms, Winding Numbers and Cauchy's Theorem

Chapter 5. Counting Zeroes and the Open Mapping Theorem

Chapter 6. Euler's Formula for sin(x)

Chapter 10. Harmonic Functions

Chapter 22. More on Brownian Motion

Off Topic