Latest revision 12-12-2022
index
C-decay Theories
$
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \SP {\quad ; \quad}
$
This what we have from Milne's Formula, actually the derivative of it:
$$
t-t_0 = (T_0-A)\ln\left(\frac{T-A}{T_0-A}\right) \hieruit \frac{dt}{dT} = \frac{T_0-A}{T-A}
$$
Here $t=$ atomic time, $T=$ orbital time,
$T_0=t_0=$ gravitational reference time, which is the "nowadays" timestamp, $A=$ gravitational timestamp in orbital time,
corresponding with a beginning (Alpha), at the time when rest mass is created out of nothing.
The speed of light $c_0$ must be assumed to be an absolute constant in atomic time. Since 1967, atomic time has
become the standard for time measurements. As a consequence, the speed of light (in empty space) cannot be varying anymore, by definition.
Whatever that is right or wrong, time period $\tau$ (= 1/frequency) and wavelength $\lambda$ are nowadays related to each other via an
invariable speed of light: $\lambda=c_0\tau$. But let's see what happened in the old days, where the speed of light $c$ has been measured
in orbital time. Let $ds$ be an infinitesimal distance in space, then according to the above:
$$
c = \frac{ds}{dT} = \frac{ds}{dt}\frac{dt}{dT} \hieruit \large\boxed{c=c_0\frac{T_0-A}{T-A}}
$$
It seems we have rediscovered Barry Setterfield's infamous law of varying light speed!
Shortly after Creation, the light speed $c$ has been close to infinity. And then it has been decaying, until attaining its
nowadays value at $T=T_0$. According to Wikipedia, that nowadays value is
$c_0 = 299\,792\,458$ metres per second and nowadays has started at $T_0=1983$. In one of the references (153.)
the following is noted: One peculiar consequence of this system of [ the 1983 ] definitions is that any future refinement
in our ability to measure $c$ will not change the speed of light (which is a defined number), but will change the length of
the meter! Or is it the length of a second? Whatever. After the year 1983, talking about a varying light speed has no sense
anymore, let it be that there have been sensible c-measurements.
Yet there is a recent book, namely [Fahr 2016],
where a variable lightspeed is still mentioned. At page 218 it reads that the speed of light would shrink with the size of the
universe according to $\,c = 1/\sqrt{R(t)}\,$ / die Lichtgeschwindigkeit
sich mit der größe des Universums wie $\,c = 1/\sqrt{R(t)}\,$ verkleinern würde [ .. ].
Such in reasonable agreement with our findings, apart from minor details - such as wrong dimensionalities. And let the cosmic scale
factor $\,a\,$ (see Hubble Parameter) always be put in place of the non-existent "magnitude of the universe"
$\,R\,$. Then write the correct formulation:
$$
\frac{c}{c_0} = \sqrt{\frac{a_0}{a(t)}} = \sqrt{\frac{m_0}{m}} = \frac{T_0-A}{T-A} = \exp\left[-\frac{1}{2} H_i (t-t_0)\right]
$$
Sideways note: conservation of Energy is upheld with orbital time.
Which is seen by combining Narlikar's Law with the law of c-decay:
$$
\frac{m c^2}{m_0 c_0^2} = \frac{m}{m_0}\left(\frac{c}{c_0}\right)^2 = \left(\frac{T-A}{T_0-A}\right)^2\left(\frac{T_0-A}{T-A}\right)^2 = 1
\hieruit \boxed{\;E = m c^2 = m_0 c_0^2\;}
$$
However, Narlikar's Law is not needed at all for Albert Einstein's famous Law to remain valid at all (orbital) times, because,
even without it, according to Time Dilation:
$$
m\,c^2 = m\,\left(c_0\frac{dt}{dT}\right)^2 = m\,\left(c_0\sqrt{\frac{m_0}{m}}\right)^2 = m_0\,c_0^2
$$
It is noticed that NO such conservation of energy can be derived for a world that is timed by atomic clocks. The above has weird consequences.
According to Length Contraction, the size of an elementary particle is inversely proportional to its rest mass.
For a rest mass approaching to zero - at the moment of creation - this means that the "volume" of an elementary particle approaches infinity,
while the energy of the particle always has remained constant in that volume. Must it be concluded that - in the limit $m/m_0 \to 0$ - the
vacuum contains the energy of all those particles that eventually will be created? In this way, empty (gravitational) space may be
full of energy, Zero-point energy?
Further suggested reading:
There has been a lot of critique from my side on Barry Setterfield's
work. It is good to notice, though, that my criticism only concerns the theory, especially as it has been exposed in the book
Cosmology and the Zero Point Energy.
The good news is that I have no trouble at all, in principle, with the data that has led to (t)his theory. Indeed the
work of Setterfield can be characterized as a monumental collection of data and facts. When seen in this way, especially chapter 3
about The Speed of Light Measurements is without doubt the most interesting and original part of the book.
But: Letting Data Lead to Theory? No! One must first have an idea about what some function is like, and only after
that it may be possible to do something with a data fit. To give an outstanding example: Quantum mechanics has originated
in this way. It has started with the hypothesis that radiation energy is emitted or absorbed in discrete packages, called quanta. And
only after that, the magnitude of Planck's constant $h$ could be determined, namely by demanding agreement with measurements. This is done
in the book The Theory of Heat Radiation at page 172. Maybe it's
possible to do something alike with Setterfield's work. We have seen that $c_0 = 299\,792\,458\,m/s$ and $T_0=1983$ year. Therefore
the only constant still to be determined there is $A$, which is the moment Alpha of "Let there be light" in orbital time.
The decay curve for c-decay is an orthogonal hyperbola with asymptote at $T=A$:
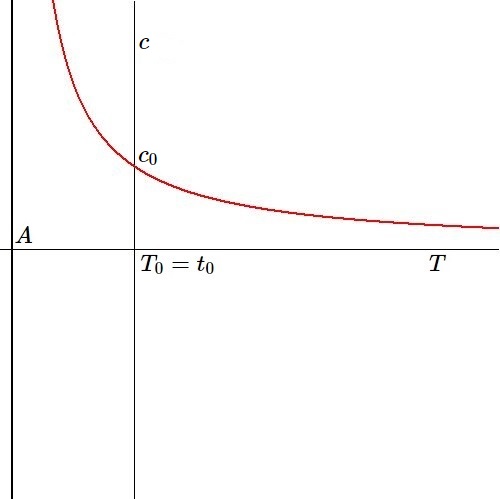
From Barry Setterfield's article The Speed of Light Curve we quote -
though Barry's picture is very different from ours:
3. The graph also represents the rate of ticking of the atomic clock against orbital time [ .. ].
The truth of the matter is, these are all the same curve.
To put it even stronger. If our theory is alright, then the varying speed of light in orbital time - also called c-decay -
is completely explained by the fact that orbital clocks and atomic clocks will be running out of sync in the long run.
The aim of lightspeed-decay has been to resolve the following, which is a problem for Young Earth Creationism.
Does Distant Starlight Prove the Universe Is Old?.
Question is: does our theory succeed in resolving the Distant Starlight problem? Let's investigate.
With atomic time it's simple: Distance $=$ lightspeed $\times$ (past time):
$$
D = c_0(t_0-t) \quad \mbox{with} \quad t < t_0
$$
In terms of gravitational time we can say something alike only for an infinitesimal distance $dD$:
$$
dD = - c.dT \hieruit D = - \int_{T_0}^{T} c_0\frac{T_0-A}{t-A} dt = - c_0\,(T_0-A)\ln\left(\frac{T-A}{T_0-A}\right)
$$
Milne's Formula is recognized immediately, so we also have that $D=c_0(t_0-t)$, as it should be.
But we have also seen that Milne's Formula is equivalent with a Hubble Parameter formula:
$$
D=\ln(1+z_i)\,c_0/H_i
$$
For small $\,z_i\,$ Hubble's Law should be reproduced:
$$
\ln(1+z_i) \approx z_i \hieruit D \approx z_i\,c_0/H_i \hieruit z_i \approx \frac{H_i\,D}{c_0}
$$
Example for Messier 87. $z_i \approx 0.00428$ ,
$H_i \approx 1/(14.4\times 10^9)\text{ year}^{-1}$ , $D \approx 65,230,000\text{ lightyears}$:
$$
0.00428 \approx \frac{65,230,000 \times c_0}{14,400,000,000 \times c_0} \approx 0.004530 \approx \mbox{ OK}
$$
Indeed our Lightspeed Decay does solve the Distant Starlight problem, though that happens in a rather trivial way.
Let's assume that $\,A = -6,000\,$ and $\,T_0 = 2,000\,$ years in:
$$
D = 65,230,000 \times c_0 = - c_0 \times 8,000\times\ln\left(\frac{T+6,000}{8,000}\right) \hieruit \\
T = 8,000\times \exp\left(-\frac{65,230,000}{8,000}\right) - 6,000
$$
Evaluate with a computer algebra system (MAPLE):
> evalf(8000*exp(-65230000/8000)-6000);
-6000.
As might be expected, because the contribution of the exponential function almost invariably can be neglected.
So, in this model, admittedly, anything has been created at 6,000 years B.C. But meanwhile something weird has happened
with the (intrinsic) Hubble parameter:
$$
H_i=\frac{2}{T_0-A} \hieruit H_i = \frac{2}{8,000} = 0.25 \times 10^{-3} \mbox{ years}^{-1}
$$
Let us now briefly consider radioactive decay, that is to say C-decay, i.e. the decay of e.g.
Carbon, which is not c-decay, the decay of lightspeed.
We know that elementary particle rest mass has been smaller in the past according to: $m < m_0$. This means that atomic clocks
have had greater ticks and thus have been running slower when compared with gravitational clocks. But radioactive decay - without
doubt - is steered by an atomic clock. To put it even stronger: radioactive decay IS an atomic clock. So we have:
$$
\frac{T_0-A}{T-A} = \frac{dt}{dT} = \sqrt{\frac{m_0}{m}} > 1
$$
This means that there have been more radioactive events $\equiv$ clock ticks between two orbital clock ticks in the past,
while measurement in atomic time ticks would show no difference with decay events as they are nowadays. With other words:
when measured in orbital time, radioactive decay has been faster in the past. Moreover, it's not difficult to see
that the curve for C-decay has the same shape as the one for c-decay: see above picture.

