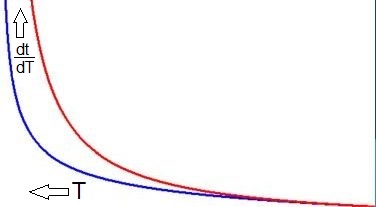

The formulae corresponding with the picture are (mind the colors):
$$
\color{blue}{\frac{dt}{dT} = \frac{1+T}{\sqrt{1-T^2}}-1} \quad ; \quad \color{red}{\frac{dt}{dT} = \frac{1}{1-T}-1}
$$
with $0 \le T \lt 1$ in reverse direction (from the right to the left instead of the reverse).
Especially in the neighborhood of present time, the relationships no not show much difference.
It should be noticed that in the Arp/de Bruijn theory the expression for the redshift
is different from the one for c-decay and for clock ticks.
Attention therefore shall be restricted to lightspeed and clock ticks, that is where our results are comparable with those by Setterfield.
With Barry's formulas we especially have:
$$
\frac{c}{c_0} = \frac{1+x}{\sqrt{1-x^2}} \met x = T
$$
With $c=$ speed of light as measured with orbital time, $c_0=$ speed of light as measured with atomic time; the latter being an absolute constant.
Let us adapt the abscissa $x$ in such a way that (1) the coordinate $T$ represents true orbital time and (2) grows from the left to the right
instead of the other way around:
$$
\frac{c}{c_0} = \frac{1+x}{\sqrt{1-x^2}} \met x = 1-\frac{T-A}{T_0-A}
$$
Then $x=1$ for $T=A$ (moment of creation) and $x=0$ for $T=T_0$ (here and now). We don't deviate from Setterfield's theory
in any respect by stating that the rate of ticking of the atomic clock against orbital time obeys exactly the same law. It also follows from
the chain rule for differentiation in combination with the definition of the speed of light speed as distance increment divided by time increment.
$$
\frac{c}{c_0} = \frac{ds}{dT}/c_0 = \frac{ds}{dt}\frac{dt}{dT}/c_0 = c_0/c_0 \frac{dt}{dT} \hieruit \\
\frac{dt}{dT} = \frac{1+x}{\sqrt{1-x^2}} \met x = 1-\frac{T-A}{T_0-A}
$$
Note that the orbital clock is synchronized with the atomic clock - i.e. they have the same "seconds" - at the here-and-now timestamp $\,T=T_0=t=t_0\,$:
$$
\left.\frac{dt}{dT}\right|_{x=0} = 1
$$
We are going to integrate the equation, that is convert from infinitesimal time intervals to continuous time. To that end we must know that:
$$
dx = d\left(1-\frac{T-A}{T_0-A}\right) = -\frac{dT}{T_0-A} \hieruit dT = -(T_0-A)dx
$$
Herewith we have:
$$
t-t_0 = \int dt = \int \frac{1+x}{\sqrt{1-x^2}}\,dT = -(T_0-A)\int \frac{1+x}{\sqrt{1-x^2}}\,dx
$$
This leaves us with a couple of elementary integrals:
$$
\int \frac{1+x}{\sqrt{1-x^2}}\,dx = \int \frac{1}{\sqrt{1-x^2}}\,dx + \int \frac{x}{\sqrt{1-x^2}}\,dx =
\arcsin(x) - \frac{1}{2} \int \frac{d(1-x^2)}{\sqrt{1-x^2}}
$$
The last term is equal to $\,-\sqrt{1-x^2}\,$, hence:
$$
t-t_0 = -(T_0-A)\left[\arcsin(x) - \sqrt{1-x^2} + C\right] \met x = 1-\frac{T-A}{T_0-A}
$$
The integration constant $C$ must be adapted in such a way that the expression is zero for $\,t=t_0\,$:
$$
\arcsin(x) - \sqrt{1-x^2} + C = \arcsin(0) - \sqrt{1-0^2} + C = 0 \hieruit C=1
$$
So finally this should be the relationship between atomic time $\,t\,$ and orbital time $\,T\,$:
$$
t-t_0 = -(T_0-A)\left[\arcsin\left(1-\frac{T-A}{T_0-A}\right)-\sqrt{1-\left(1-\frac{T-A}{T_0-A}\right)^2}+1\right]
$$
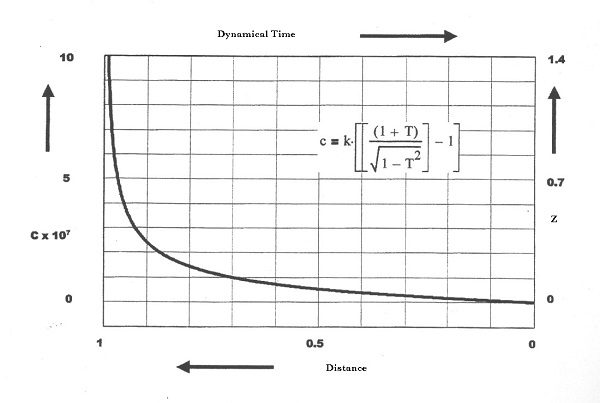
In Setterfield's book at page 190 we have the formula (65),
which would be the same upon substitution $\,T\to x\,$. There is a (not so) small detail, though, which is the constant $K$:
$$
\int \left[(1+T)/\sqrt(1-T^2)\right]dt = K\left[\arcsin T -\sqrt(1-T^2)+1\right] \met K = 4.745 \times 10^9
$$
A huge fudge factor $K$, which is taken completely out of thin air, is supposed to take care of elongation of atomic time, such
that the Big Bang at 13,7 billion years B.C. (atomic time) would be coincident with Creation at 8,000 B.C. (gravitational time).
This outcome is employed in ANCIENT CHRONOLOGY IN SCRIPTURE. Alas.
Herewith the synchronization of the two clocks at present time is completely destroyed. One atomic second would be the same as
billions of gravitational seconds, here and now, which is nonsense:
$$
\left.\frac{dt}{dT}\right|_{T=0} = K
$$
Once more it is clear that Setterfield is not able to manage the consequences of his own theory.
But let's simply abandon the fudge factor $K$ and proceed nevertheless.
A graphical representation of atomic time as a function of gravitational time according to the Setterfield/Kiel theory is painted
blue. Such in comparison with the same according to the Arp/deBruijn theory in
red. Then we see something remarkable: at the blue curve the atomic
time $t$ starts at a finite value, though with an infinite derivative. The latter could be interpreted as inflation.
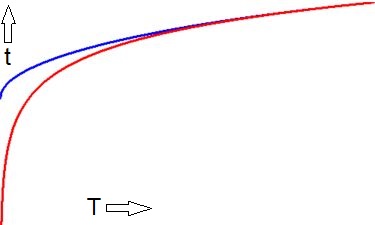
Let us take a look at the atomic time $\,t=t_A\,$ at the moment of creation in gravitational time $\,T=A\,$. Then $x=1$ or: $$ 1-\frac{T-A}{T_0-A} = 1 \hieruit t_A-t_0 = -(T_0-A)\left[\arcsin(1)-\sqrt{1-1^2}+1\right] \hieruit \\ t_A = T_0 - (T_0-A)\left[\frac{\pi}{2}+1\right] \hieruit t_A = A - \frac{\pi}{2}(T_0-A) $$ Suppose that the moment of creation is $A = -8000$ and the here and now timestamp is $T_0 = 2018\,$, then we have: $$ t_A \approx -8000 - \pi/2 \times (2018+8000) \approx 23,736 \; \mbox{years B.C.} $$ Hence Creation in atomic time must have taken place at approximately 23 thousand years before Christ. Should this be interrpeted as the (atomic) year of the Big Bang then? I don't think that anybody will be pleased with this outcome, neither in secular or in YEC circles. But let's do it the other way around. Suppose that the Big Bang is at $t_A = 3,7$ billion years B.C. and the here and now timestamp is the same. Then we have for Alpha, the moment of creation: $$ T_0-A = \frac{t_0-t_A}{\pi/2+1} \hieruit A = 1,439,239,957 \mbox{ years B.C.} $$ Hence creation in gravitational time, according to the Setterfield/Kiel theory with correct mathematics this time, must have taken place at approximately 1,4 billion years before Christ.
The following diagram by Rinus Kiel may be regarded as a lucid pictural summary of Barry Setterfield's theory, in a nutshell:
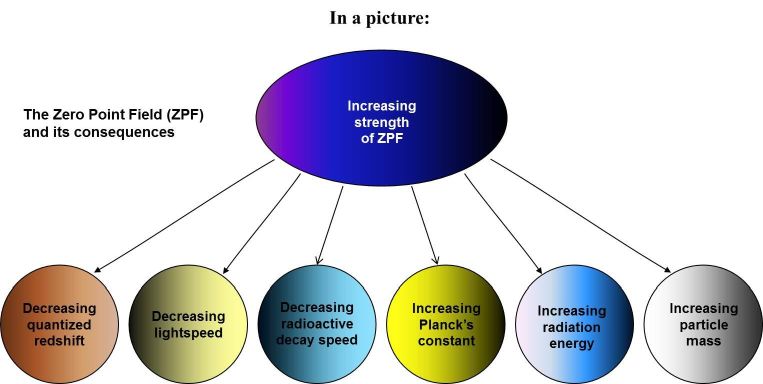
Also note that the effects, thought as being caused by the ZPE, may be regarded as a rather accurate implementation of the Creationist Wish List. Does it mean that they are simply a product of wishful thinking? Not necessarily so, as has been demonstrated:
However, according to our own highly speculative theory, the Zero Point Energy is not
causing any of the phenomena, such as those depicted in the above diagram. It rather should
be the other way around. According to us, cause and effect have been mixed up with
Cosmology and the ZPE.
Increasing particle mass should be on top as the cause; increasing strength of ZPE - if it
real - should be at the bottom as one of the effects. And the Planck constant is assumed to be
an absolute constant, as there is only one hypothesis instead of several ones, namely
the increasing particle mass. It is the minimalist position, as it is called by Setterfield.
The resemblance with the original diagram by Rinus Kiel is striking, while I have done not
any attempt to impose wishful thinking upon my little theory (at least I hope so).
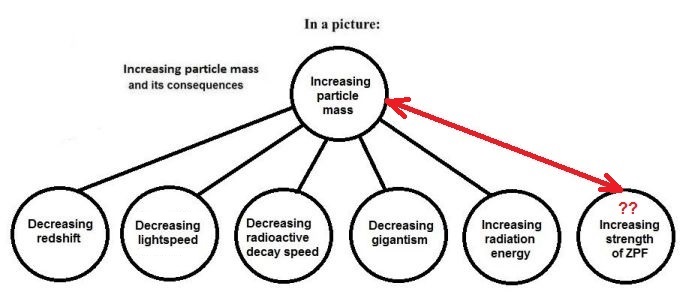
As has been said, essentially the only difference between the two diagrams is the exchange of
cause and effect: (Increasing strength of ZPF) $\color{red}{\Longleftrightarrow}$
(Increasing particle mass).
This could be marked in some circles as a quite satisfactory achievement. It must be noticed,
however, that I've been talking about a ZPE and not about a ZPF all the time.
The reason for this being that the existence of a real Zero Point Energy has been verified
experimentally for fields with a material substrate; for example vibrating molecules in a
solid do indeed have a real ZPE. But the existence of a Zero Point Energy for the vacuum
- Zero Point Field - IMHO remains questionable.
Hence the question marks ($\color{red}{??}$) in the bottom diagram.
It should be emphasized that Setterfield's mantra "Letting Data Lead to Theory" is not in any way invalidated by turning (t)his theory - in fact: any theory - upside down. In particular it has no effect, at all, on the data themselves! So what's the big deal? If one has to choose between a little, minimalist theory that is at least mathematically correct? Or an overly complicated, multi-layer, unmanageable theory that has turned out to be not even wrong?
(+) Rinus may be regarded as my cosmic twin brother. Despite our differences, we had many things in common.