Latest revision 16-11-2023
index
$
\def \MET {\quad \mbox{with} \quad}
\def \SP {\quad \mbox{;} \quad}
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \EN {\quad \mbox{and} \quad}
\def \OF {\quad \mbox{or} \quad}
\def \half {\frac{1}{2}}
$
Let there be CMB
Essential reading is: Self Energy Field. There we found for the gravitational self energy density
$$
u_G = - GM^2/(8\pi r^4)
$$
Integrating from the rim of our Observable universe towards infinity:
$$
U_G = \int_{R_O}^\infty \left[ - \frac{G M_O^2}{8\pi r^4} 4\pi r^2 \right] dr = - \frac{G M_O^2}{2}\int_{R_O}^\infty \frac{dr}{r^2} = - \frac{G M_O^2}{2R_O}
$$
The latter outcome is also known from the booklet Relativity Reexamined by Léon Brillouin: formula (7.13) times $c^2$.
But now it goes wrong because, due to $E=mc^2$, energy has a mass. Therefore we must integrate the energy density according to the Variable Mass Theory; we cannot assume that it's a constant. The total gravitational self energy of the observable universe herewith becomes
$$
U_G = - \frac{G M_O^2}{2} \int_{R_O}^\infty \frac{e^{-H/c.r}}{r^2}dr = - \frac{G M_O^2}{2R_O}.W.\mbox{VMT}
$$
Computing the integral by hand is a bit difficult, but we let a Computer Algebra System (MAPLE) do the work.
$$
\mbox{VMT} = \int_W^\infty \frac{e^{-x}}{x^2}dx = \frac{e^{-W}}{W} - \mbox{Ei}(W) \quad \mbox{with} \quad \mbox{Ei}(x) = \int_1^\infty \frac{e^{-xt}}{t}dt
$$
Especially take notice of $\int_{R_O}^\infty = \int_W^\infty$, meaning that the integral is not over the observable universe
but over the infinite and eternal rest of it. This would mean that the only place where the energy $U_G$ can be observed eventually
is precisely at the horizon of the observable universe. And that observation must be accompanied with the maximum redshift, because
it "sees" something at that rim (= horizon) and because there is no larger redshift available.
@Francois-Zinserling .
My approach insists that an aether must exist [ .. ]
My approach insists that an gravitational (self) energy field must exist (I'm not sure about a proper name). But it may be that we are talking about the same thing. And if such is the case, then a more detailed account of the properties of our "aether" is given in Self Energy Field. It is shown beneath the last horizontal rule in the webpage that in the neighborhood of our sun this Energy Field / your Aether might provide an alternative explanation for the Perihelion precession of Mercury.
It has been derived that mass and radius of our so-called Observable universe are respectively given by
$$
M_O = \frac{W}{2}\frac{c^3}{G.H} \quad ; \quad R_O = W\frac{c}{H} \quad \mbox{where} \quad W = 3.383634283
$$
$c=$ lightspeed, $G=$ gravitational constant, $H=$ Hubble parameter. Numerically: $M_O \approx 2.87\times 10^{53}\mbox{ }kg$, $R_O \approx 4.26\times 10^{26}\mbox{ }m$.
But the Aether itself contains gravitational field energy and therefore it has also a mass, which is derived to be
$$
M_A = - \frac{G}{c^2}\frac{M_O^2}{2R_O}.W.\mbox{VMT} \quad \Longrightarrow \quad
-\frac{M_O}{M_A}=\left(\frac{1}{4}W^2.\mbox{VMT}\right)^{-1} \approx 15.47019772
$$
The mass of our thus defined Aether is roughly fifteen times smaller and negative when compared with the Observable mass.
Let's proceed with a firm disclaimer, as expressed by Louis Marmet via A Cosmology Group
(18 dec. 2022 04:23): How many 'effects' are required to explain the CMB? 12? 20? I fall asleep reading these
arguments based on a contrived set of explanations that are just as unlikely as the other ... To me, it's a sign of bad science -
you are not missing much ;-) Abort, Retry, Fail?
If there is something in the universe which has a uniform mass / energy density and provides sort of a rest frame at the same time,
then it certainly is the Cosmic Microwave Background.
According to the Stefan-Bolzmann law of thermal radiation,
the energy density of the CMB is given by equation (78) in a book by Max Planck:
THE THEORY OF HEAT RADIATION.
Symbols are: $u=$ energy. $\sigma=$ Stefan-Boltzmann constant,
$\Theta=$ CMB temperature (Kelvin), $m=$ mass, $V=$ volume. Because we are talking about volumes, not a surface in space, according to
Wikipedia: the radiation constant
(or radiation density constant) $\,a=4\sigma/c_0\,$ must be employed.
$$
u_{CMB} = a\,\Theta^4
$$
On the other hand, we have the gravitational Self Energy Field with a total energy
$$
U_G = - \frac{G M_O^2}{2R_O}.W.\mbox{VMT}
$$
We are not going to spend much of eloquent proze on the subject. Instead it is simply assumed that
Uniform CMB energy + Gravitational self energy = 0
Where, according to the above, we thought that
$$
U_{CMB} = \frac{4}{3}\pi R_O^3.\frac{4\sigma}{c}\Theta^4
$$
@ExpEarth (Matthew Edwards) writes:
I argue that the energy lost in the redshift of the CMB goes into gravity.
No Matt, though your writeups have been very inspiring, I find that it is exactly the other way around.
There is a gravitational self-energy field surrounding the mass of the observable universe.
That self-energy itself is equivalent with a remote mass and therefore the CMB it emits is redshifted.
Tired Light models would make the CMB be redshifted along its trip towards the observer, which is not.
According to the Variable Mass Theory (VMT),
it is redshifted at the rim of the Observable universe.
So gravity goes into the CMB. And the latter is uniform everywhere inside the Observable universe.
Previous theory went wrong because, according to the VMT, volumes must be calculated in a non-Euclidean way.
VMT actually replaces GR; so apparent (GR-like) distortion of volumes is less strange than it may seem at first sight.
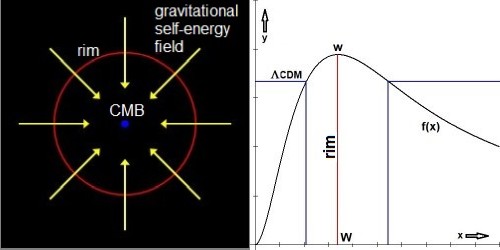
We repeat the most important results from the previous. A purely mathematical result first:
$$
f(x) = \frac{2-e^{-x}(x^2+2x+2)}{x} \quad \mbox{with} \quad W = 3.383634283 \quad \mbox{and} \quad w = f(W) = 0.3883945571
$$
For the mass $M_O$ and radius $R_O$ of our Observable universe we find (with $c=$ lightspeed, $G=$ gravitational constant, $H=$ Hubble parameter):
$$
M_O = \frac{W}{2}\frac{c^3}{G.H} \quad \mbox{;} \quad R_O = W\frac{c}{H}
$$
The total gravitational self energy of our Observable universe has been correctly calculated so far, but as a Variable Mass
(with $E=m_0c^2$) it is redshifted as it enters the horizon (also called the rim), in the form of CMB radiation.
That redshift canot be else than the maximal observable one, namely $1+z_{max} = e^W$ and so:
$$
U_G = - \frac{G M_O^2}{2R_O}.W.\mbox{VMT} / e^{W} \quad \mbox{where} \quad \mbox{VMT} = \int_W^\infty \frac{e^{-x}}{x^2}dx
$$
Furthermore it went wrong (with $\sigma=$ Stefan-Bolzmann constant, $\Theta=$ temperature) at the place where we thought that
$$
U_{CMB} = \frac{4}{3}\pi R_O^3.\frac{4\sigma}{c}\Theta^4
$$
When multiplied with mass density instead of radiation density, the mass of the Observable universe can never be greater than the mass of the whole Universe. The latter has been calculated in an earlier stage. We must substitute $\rho_0 \to 4\sigma/c.\Theta^4$ and then formulate correctly instead (with $x=W.c/H$ ):
$$
U_{CMB} = \frac{4\sigma}{c}\Theta^4 \int_0^{R_O} e^{-H/c.r}.4\pi r^2.dr =
\frac{4\sigma}{c}\Theta^4 \left(\frac{c}{H}\right)^3 4\pi \int_0^{W} e^{-x}x^2.dx \\
= \frac{4\sigma}{c}\Theta^4 \left(\frac{c}{H}\right)^3 4\pi \left[\frac{2-e^{-W}(W^2+2W+2)}{W}\right]W =
4\pi.wW \left(\frac{c}{H}\right)^3 \frac{4\sigma}{c}\Theta^4
$$
Leading to the following end-result.
$$
4\pi.wW \left(\frac{c}{H}\right)^3 \frac{4\sigma}{c}\Theta^4 =
G\left[\frac{W}{2}\frac{c^3}{G.H}\right]^2\frac{W.\mbox{VMT}/e^W}{2(W.c/H)} \\
\frac{4\sigma}{c}\Theta^4 = \frac{W^2.\mbox{VMT}.e^{-W}}{32\pi.wW}\frac{(Hc)^2}{G}
$$
W := 3.383634283;
G := 6.67408*10^(-11);
Mpc := 3.08567758*10^22;
H := 73.4; # Riess
H := H*1000/Mpc;
c := 299792458;
VMT := int(exp(-x)/x^2,x=W..infinity);
sigma := 5.670374419*10^(-8);
wW := 2-exp(-W)*(W^2+2*W+2);
u_G := W^2*VMT/(32*Pi*wW)*(H*c)^2/G;
u_G := u_G*exp(-W); # But I'm not sure
Theta := evalf((c/(4*sigma)*u_G)^(1/4));
Theta := 2.764453563
The small discrepancy with experiment that is remaining can easily be explained by the uncertainty of the Hubble parameter.
Calculating the other way around:
Theta := 2.726;
H := sqrt((G/c^2)*(32*Pi*wW)/(W^2*VMT*exp(-W))*4*sigma/c*Theta^4);
H := evalf(H/1000*Mpc);
H := 71.37221336
Which is compatible with the Hubble tension.
No expanding space-time, no Big Bang, no Co(s)mic Inflation, no Primordial Relic Radiation, no fuzz parameters, no tweaking, no nothing of the kind. And yet an accurate estimate of the Cosmic Microwave Background Θemperature.
The self-energy of an electric field has been tentatively used for calculating the Electromagnetic Mass of an electron.
We can prove that something like this does not work for the gravitational field. Charge is not mass in the first place. And the gravitational field has negative mass. If we assume that the mass of the field adds up to / is substracted from the common mass then that common mass shall be corrected as follows.
$$
M_O := \frac{c^3}{G.H}\frac{W}{2} - \frac{c^5}{G.H.c^2}\frac{W^2}{8}W.\mbox{VMT}.e^{-W} = M_O \left(1-\frac{W^2}{4}\mbox{VMT}.e^{-W}\right)
$$
Thus giving rise to an iterative process of the form $M_O := M_O(1-g)$ where $g=0.1915329972\times 10^{-3}$.
Suppose for example that the zero value is approached one percent, then we have for the number of iterations
$$
n = \frac{\ln(0.01)}{\ln(1-g)} \approx 24,042
$$
It takes quite some time - in mathematics, not in physics.
But in the end the mass $M_O$ of the observable universe turns out to be zero:
$$
\lim_{n\to\infty}M_O(1-g)^n=0
$$
Which is of course nonsense. The mass of the field does not combine with the common mass. There must exist another mechanism for converting the self-energy of gravitation into something. That something is conjectured to be the CMB.
It has been shown in A Special Escape that the mass $M$ of (for example) the observable universe inside,
via the escape velocity, must be augmented as well. Resulting in a mass $M'$ which is the original $M$ plus the negative mass of its
Self Energy Field:
$$
v=\sqrt{\frac{2GM}{R}-\left(\frac{GM}{Rc}\right)^2}=\sqrt{\frac{2GM'}{R}} \quad \mbox{with} \quad M' = M + \left[-\frac{GM^2}{2Rc^2}\right]
$$
Therefore Special Relativity would enable the above disastrous iteration process to proceed, if it were not that the Self Energy Field
is neutralized by a positive energy field, which may be conjectured to be the CMB again.
But how can the latter be redshifted by $e^{-W}$ now? We could argue that our theory is in some sense analogous to the Big Bang story.
Trying to tell everybody that the CMB is primordial, a relic, with maximal redshift. The latter, in our case, is inevitably limited
with the factor $e^{-W}$ . Then we are done, aren't we ?
Whatever. When specified for the Observable universe we obtain
$$
M'_O = \frac{W}{2}\frac{c^3}{G.H}(1-g) \quad ; \quad g = \frac{W^2}{4}\mbox{VMT} \quad ; \quad R_O = W\frac{c}{H} \\
v = \sqrt{2G\frac{W}{2}\frac{c^3}{G.H}\frac{H}{Wc}(1-g)} \hieruit \Large\boxed{v = c\sqrt{1-g}} \normalsize \approx 0.9671398994 \times c
$$
With Special Relativity, the escape velocity from the Observable universe is calculated to be slightly less than the speed of light.
As a consequence, light can escape from - as well as enter into - that part of the universe.
With the relic radiation as a paradigm, the discrepancy with lightspeed becomes even smaller:
$$
g = \frac{W^2}{4}\mbox{VMT}.e^{-W} \hieruit v = c\sqrt{1-g} \approx 0.9989029695\times c
$$
The idea that the Cosmic Microwave Background is not originating from particles (protons) is consistent with modern science,
as expressed in the book by [Fahr 2016] at page 157:
Ein weiteres Mysterium bei der konventionellen Erklärung des CMB-Hintergrundes verbirgt sich in dem heute
damit verbundenen Zahlenverhältnis von CMB-Photonen zu Baryonen (Protonen). Die Zahl der CMB-Photonen ist nämlich
erheblich viel größer als die Zahl der Protonen, obwohl die Ersteren aus den Letzteren und ihren Antiteilchen dereinst
einmal duch Annihilationsprozesse herforgegangen sein wollen.[ .. ] With help of Google translate: Another mystery
in the conventional explanation of the CMB background is hidden in the numerical ratio of CMB photons to baryons (protons) associated
with it today. The number of CMB photons is considerably larger than the number of protons, although the former are claimed to have
emerged from the latter and their antiparticles through annihilation processes.
Why does the CMBR show such a precise black-body radiation
spectrum? No elementary particles are involved with its birth, just gravity and photons. So what else could the spectrum have been?
There is a more rigorous argument, though. According to Planck's law (Wikipedia)
the spectral radiance of a body for frequency $\,\nu\,$ at absolute temperature $\,\Theta\,$ is given by
$$
B(\nu,\Theta) = \frac{2h\nu^3}{c^2}\frac{1}{\exp\left(\frac{h\nu}{k_B\Theta}\right)-1}
$$
where $\,k_B\,$ is the Boltzmann constant, $\,h\,$ is the Planck constant, and $\,c\,$ is the speed of light in vacuum.
With the Variable Mass Theory, frequency and temperature are subject to change as has been explained in our
Support by Hoyle section. The other quantities remain constant.
$$
\frac{\nu}{\nu_0} = \frac{\Theta}{\Theta_0} = \frac{m}{m_0} \hieruit \frac{B}{B_0} = \left(\frac{m}{m_0}\right)^3 = (1+z_i)^{-3}
$$
Leading to the important conclusion that black body radiation is invariant with varying elementary particle (rest) mass.
More precisely: the magnitude of the spectral radiance may be different, but the shape of its distribution does not change.
Very much the same is expressed by Wien's displacement law ($\lambda=$ wavelength) which turns out to be invariant as well.
$$
x \equiv \frac{h\,c}{\lambda_{peak}\,k_B\,\Theta}
\quad \mbox{with } \,x\, \mbox{ as the (dimensionless) solution of} \quad (x-5)\,e^x+5=0 \\
\frac{m}{m_0} = \frac{\Theta}{\Theta_0} = \frac{\lambda_0}{\lambda} \hieruit
\frac{h\,c}{\lambda_{peak}} = x\,k_B\,\Theta \quad \mbox{with} \quad x = 4.965114231744276304
$$

