index $ \def \MET {\quad \mbox{with} \quad} \def \EN {\quad \mbox{and} \quad} \def \SP {\quad \mbox{;} \quad} \def \OF {\quad \mbox{or} \quad} \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} $
We begin the derivation process with the introduction of the standard Newtonian formula for gravitational potential energy
$$
\Phi = -\frac{G M m_0}{R} \qquad (1)
$$
where $\Phi$ is the gravitational potential energy, $G$ is the gravitational constant, $M$ is the mass of the primary celestial body, $m$ is the rest mass of a secondary object and $R$ is the radial distance from the object to the center of mass of the celestial body. Then, using the special relativity Lorentz gamma factor
$$
\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} \qquad (2)
$$
often designated by the Greek symbol $\gamma$ where $v$ is the relativistic speed of an object and $c$ is the speed of light, we apply it to the right side of equation (1) to obtain
$$
\Phi = -\frac{G M m_0}{R}\frac{1}{\sqrt{1-\frac{v^2}{c^2}}} = -\frac{G M m_0}{R\sqrt{1-\frac{v^2}{c^2}}} \qquad (3)-(4)
$$
For our next step in the derivation process we employ the special relativity formula for relativistic kinetic energy
$$
K = \frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}} - m_0c^2 \qquad (5)
$$
where $K$ gives the correct value for kinetic energy at all speeds of $v$ from $0$ to $c$. We then follow the standard procedure of equating the difference between kinetic energy and gravitational potential energy to 0 as shown
$$
0 = \frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}} - m_0c^2 - \frac{G M m_0}{R\sqrt{1-\frac{v^2}{c^2}}} \qquad (6)
$$
where we now show the minimum relativistic escape energy and not the minimum Newtonian escape energy needed to overcome the gravitational force of a celestial body of mass $M$. This then gives
$$
\frac{G M m_0}{R\sqrt{1-\frac{v^2}{c^2}}} = \frac{m_0c^2}{\sqrt{1-\frac{v^2}{c^2}}} - m_0c^2 \qquad (7)
$$
that when solved for $v$ using a computer mathematical application is ridiculous. It can be easily done by hand.
$$
m_0c^2 - \frac{G M m_0}{R} = m_0c^2\sqrt{1-\frac{v^2}{c^2}}
$$
It is noticed that there is a removable singularity for $v=c$, mathematical but not physical. Continuing story:
$$
\left(1 - \frac{G M}{R c^2}\right)^2 = 1-\frac{v^2}{c^2} \\
v = c\sqrt{1 - \left(1 - \frac{G M}{R c^2}\right)^2} = \sqrt{\frac{2GM}{R}-\left(\frac{GM}{Rc}\right)^2}
$$
So the escape velocity according to Special Relativity is
$$
v=\sqrt{\frac{2GM}{R}-\left(\frac{GM}{Rc}\right)^2}=\sqrt{\frac{2GM'}{R}} \quad \mbox{with} \quad M' = M + \left[-\frac{GM^2}{2Rc^2}\right]
$$
The term between square brackets is recognized as the - Newtonian ! - negative mass of the Self Energy Field of the same body with radius $R$ and mass $M$.
Due to the SR formulation, the escape velocity $v$ cannot exceed the speed of light $c$ :
$$
c \ge v \quad \Longleftrightarrow \quad \frac{2GM}{R}-\left(\frac{GM}{Rc}\right)^2 \le c^2
$$
$$
R^2-2\frac{GM}{c^2}R+\left(\frac{GM}{c^2}\right)^2 \ge 0 \quad \Longleftrightarrow \quad \left(R-\frac{GM}{c^2}\right)^2 \ge 0
$$
Which is invariably true. For the special case $v=c$ we have
$$
m_0c^2 - \frac{G M m_0}{R} = m_0c^2\sqrt{1-\frac{v^2}{c^2}} = 0 \hieruit R-\frac{G M}{c^2}=0
$$
With SR and half the Schwarzschild radius $R_N$ ($_N=$ Newtonian) we are not running into the same problems as with General Relativity and the "old" Schwarzschild radius.
$$
R_N = \frac{G M}{c^2}
$$
There is an interesting detail in
The theory of Heat Radiation by Max Planck, where at page 49 and
following Maxwell's radiation pressure is calculated. There are two equations for the force exerted by the radiation pressure,
the correct one (64) as derived from Maxwell's equations (wave model), and an incorrect one at the bottom of page 57, which is derived
from a model of light with particles (photons). Quote: On comparing this relation with equation (64) in which
all symbols have the same physical significance, it is seen that Newton's radiation pressure is twice as large as Maxwell's
for the same energy radiation. Sure, but the kinetic energy of Newton's photons in (68) is assumed to be $mc^2/2$, while
according to modern insights (from Special Relativity) it should be $mc^2$. This removes all discrepancies between the wave and the particle
model for light and it makes Planck's conclusions at page 58 obsolete.
However, there is an important lesson to be learned. A piece of theory which is generally attributed to General Relativity is the
Schwarzschild radius, which also has been employed in the above theory.
It is possible to derive it in Newtonian mechanics as well, by equating kinetic energy to potential energy, thus giving the so-called
Escape velocity. For light we derive
$$
\frac{1}{2}mc^2 = \frac{G\,M\,m}{R_M} \hieruit R_M = 2GM/c^2
$$
However, the exercise with Planck's Heat Radiation has teached us to use instead
$$
mc^2 = \frac{G\,M\,m}{R_N} \hieruit R_N = GM/c^2
$$
Giving a Newtonian radius which is twice as small as the one derived by GR. Let's be daring and adopt it as the correct one.
Now what are the consequences?
Repeating and adapting all formulas in this section would be boring. we will therefore skip most of
the results in this section and go straight to the most relevant one, namely
$$
f(x) \lt \frac{H^2}{4\pi\,G\,\rho_0} \quad \mbox{instead of} \quad f(x) \lt \frac{H^2}{8\pi\,G\,\rho_0}
$$
The following possibilities in the Origin of Inertia section are repeated again.
$$
H^2 = \chi\,G\,\rho_0 \MET
\begin{cases}
\chi = \pi & (: \mbox{OI}) \\ \chi = 4\pi/3 & (:\mbox{Mach}) \\ \chi = 8\pi/3 & (: \Lambda\mbox{CDM})
\end{cases}
$$
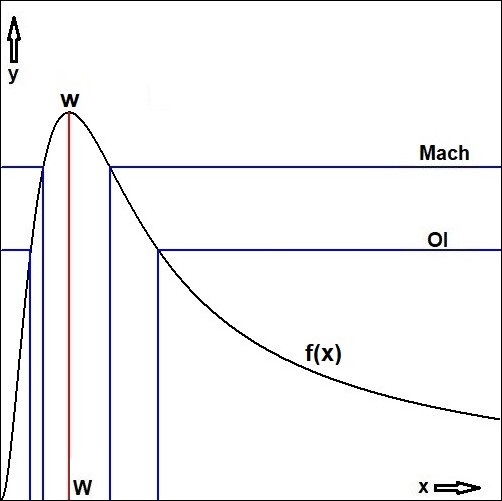
Respectively resulting in:
$$
\begin{cases}
f(x) \lt 1/4 \; : & x \lt 1.470720414 \OF x \gt 7.879101243 & (: \mbox{OI}) \\
f(x) \lt 1/3 \; : & x \lt 2.096433787 \OF x \gt 5.451457921 & (: \mbox{Mach}) \\
f(x) \lt 2/3 \; : & \mbox{for all } x \mbox{ because of } f(x) < 0.3883945571 & (: \Lambda\mbox{CDM})
\end{cases}
$$
In short: ΛCDM is replaced everywhere by Mach and the results for OI are different from the previous.
