Poreus Continuüm

• On the role of applied PDE analysts in non-academic R&D workplaces

Teneinde de primaire stroming en de temperatuurverdeling in een warmtewisselaar te beschrijven, hebben onderzoekers het zogenaamde vloeistof-pijpen continuüm model bedacht. Het idee hierachter is ontleend aan de klassieke theorie der poreuze media. Hierbij kan worden gedacht aan transportverschijnselen in lagen van zand, klei en leem. Toepassingen hiervan vindt men in de hydraulica van grondwater. Maar wie goed om zich heen kijkt, ziet vele andere transportverschijnselen waarbij poreuze media een rol spelen. Zoals aardappelen, opgeslagen in een silo, die een poreus medium vormen voor luchtkoeling. Andere voorbeelden zijn filtratie en chemische reakties waarbij vaste katalysatoren worden gebruikt. Maar ook stroming in de kern van een nucleaire reaktor, of in de pijpenbundel van een warmtewisselaar, kan met enige verbeeldingskracht beschouwd worden als stroming in een poreus medium. Het heeft voordelen om pijpenbundels op deze manier te modelleren omdat het, vanuit een praktisch oogpunt, ondoenlijk is om de grondvergelijkingen van de stromingsleer (Navier-Stokes), en de vergelijkingen die de warmteoverdracht beschrijven, rechtstreeks toe te passen. Denk alleen maar aan de randvoorwaarden voor de snelheden. Die zouden dan nul moeten zijn in ieder punt van een gecompliceerde vaste struktuur.

Alvorens verder te gaan is het goed om op te merken dat er niets op tegen is om een pijpenbundel te beschouwen als een echt continu medium. Het vloeistof - pijpen continuüm is niet wezenlijk verschillend namelijk van andere continue media, zoals ijzer, water, lucht of de ruimte-tijd zelf. Wij hebben op andere plaatsen van deze website gezien dat ook "echte" continue media helemaal onderaan voorzien zijn van een corpusculaire struktuur. Fysisch kunnen continue media alleen maar bestaan als benadering, hetgeen zijn weerspiegeling vindt in het feit dat de reële getallen, die met onze waarneming van het continuüm overeenkomen, wezenlijk onnauwkeurig zijn. Betrekken wij dit op het vloeistof-pijpen continuüm, dan moet konkreet rekening gehouden worden met een onnauwkeurigheid in de orde van de afstand tussen (de assen van) twee naburige pijpen, de zogenaamde "steek" van de pijpenbundel.

Er wordt van uitgegaan dat het primaire stromingsveld in eerste benadering incompressibel, en ook rotatievrij is. Het laatste kan intuïtief worden begrepen als volgt. De afmetingen van een vloeistofdeeltje in het model zijn, min of meer per definitie, groter dan de steek. De afstand tussen twee naburige pijpen komt immers overeen met de infinitesimale afstand in dit continuüm. Het is redelijk te veronderstellen dat een vloeistofdeeltje van deze grootte een wrijving zal ondervinden die aan beide zijden vrijwel hetzelfde is, en dus niet zal roteren. Als gevolg hiervan zijn de (partiële differentiaal)vergelijkingen voor stroming in een pijpenbundel in eerste benadering hetzelfde als voor een ideale stroming (in cylindercoördinaten wel te verstaan): $$ \frac{\partial ru}{\partial r} + \frac{\partial rv}{\partial z} = 0 \qquad ; \qquad \frac{\partial v}{\partial r} - \frac{\partial u}{\partial z} = 0 $$ Hierin is: $u =$ horizontale snelheidkomponent, $v =$ vertikale snelheidscomponent, $r =$ straal, $z =$ vertikale afstand.

Nog grover, maar in wezen niet erg afwijkend van het ideale stromingsmodel, is de werkwijze die werd gevolgd door de afdeling TA/K bij Neratoom . Dit was een Technische Afdeling die bestond uit Constructeurs, mensen aan het tekenbord, zonder academische opleiding. Zij hadden het volgende beeld van de stroming bij het in- en uittree-gedeelte van de pijpenbundel (de figuur is voor tweeërlei uitleg vatbaar, waarvan er maar één de juiste is):

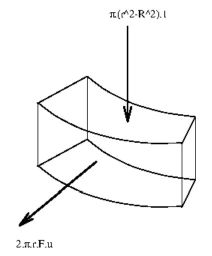
Beschouw een ringvormig vloeistofelement in het uitstroomgebied. De binnenstraal van dit element is gelijk aan de (buiten)straal $R$ van de centrale pijp. De buitenstraal van de ring heet $r$ en is variabel. De hoogte van de ring is gelijk aan de hoogte van de uitstroomperforatie $F$. Zowel de achterkant van de ring (centrale pijp), als de onderkant (pijpplaat) zijn afgesloten. Zodoende moet de flux door de bovenkant steeds gelijk zijn aan de flux door de voorkant. Gemakshalve wordt aangenomen dat het medium de ring binnenstroomt met de midden-bundel snelheid. Daarvoor wordt een konstante waarde $1$ aangenomen. De snelheidskomponent $u$ kan nu eenvoudig worden berekend uit: $$ \pi.(r^2 - R^2).1 = 2.\pi.r.F.u \qquad \Longrightarrow \qquad u = \frac{r^2 - R^2}{2.F.r} = \frac{1}{2.F} \left( r - \frac{R^2}{r} \right) $$ Ter plaatse van de uitstroom-perforatie geldt het totale massabehoud van de stroming die uit de midden-bundel komt en de stroming die door de perforatie naar buiten treedt.

We zullen nu laten zien dat dit primitieve stromingsbeeld niettemin overeenkomt met de benadering van TA/SWO, de Technische Afdeling voor Stroming en WarmteOverdracht, waar ik zelf werkzaam was. We zagen dat de stroming in eerste benadering onsamendrukbaar en rotatievrij mag worden verondersteld. Neem voor de komponent $v$ aan dat ze lineair toeneemt in axiale richting $z$, dat is de eenvoudigst mogelijke aanname. De andere komponent $u$ kennen we al: $$ v = - \frac{z}{F} \qquad ; \qquad u = \frac{ r^2 - R^2}{2.F.r} $$ De lezer kontroleert gemakkelijk dat deze oplossing inderdaad voldoet aan de partiële differentiaalvergelijkingen die de ideale stroming beschrijven. Toch is er een maartje aan dit verhaal. Aan de bovenkant van de perforatie $F$ namelijk gaat het lineaire verloop van vertikale komponent $v$ met een knik over in $v=-1$ en wordt de horizontale komponent $u$ plotseling $0$. Dit is fysisch uiteraard onmogelijk. Op grond van de juiste randvoorwaarden zal de academische oplossing van het stelsel een ander beeld te zien geven. En zeker ter plaatse van de overgang naar midden-bundel zal het verschil met de tekenzaal aanpak goed te zien zijn. Maar als eerste klap? Zeker een daalder waard!

Sla een controle volume om een aantal pijpen heen en zet de energiebalans op voor dit volume. Laat vervolgens het volume "infinitesimaal klein" worden, hoewel het altijd groter moet blijven dan de steek. Of gooi de integraaltekens weg, na het theorema van Gauss te hebben toegepast. Of pas een willekeurige andere verwaarlozingstechniek toe. Dan wordt hiermee "afgeleid" het volgende stelsel partiële differentiaalvergelijkingen van de eerste orde, geldig voor de temperaturen: $$ c.G_P \left[ u.\frac{\partial T_P}{\partial r} + v.\frac{\partial T_P}{\partial z} \right] + a.(T_P - T_S) = 0 \qquad \mbox{: primair} $$ $$ c.G_S.\frac{\partial T_S}{\partial z} +a.(T_S - T_P) = 0 \qquad \mbox{: sekundair} $$ Hierin is: $c=$ warmtecapaciteit; $G=$ massastroom; $T=$ temperatuur; $(r,z)=$ cylindercoördinaten; $(u,v)=$ genormeerde snelheden; $a=$ totale warmteoverdrachtscoëfficient; $P=$ primair; $S=$ sekundair. De randvoorwaarden mogen niet worden vergeten: $$ T_P = T_{PL} \qquad \mbox{bij de primaire inlaat (intreeperforatie boven)} $$ $$ T_S = T_{S0} \qquad \mbox{bij de sekundaire inlaat (pijpplaat onder) } $$ Het stelsel vergelijkingen dient als raamwerk waarop een eindige Volume methode gebaseerd kan worden. Alsof je eerst meel maakt van aardappelen en daarna weer aardappelen van het meel (ik citeer S.V. Patankar). Aan de andere kant is het zinvol om een aantal zaken helemaal analytisch te benaderen.

Er is nog een ander argument waarom een ideale inwendige stroming letterlijk ideaal is voor het uitrekenen van de temperatuurverdeling in een warmtewisselaar. Het volgende is een toepassing van de ongelijkheid van Schwarz voor het inprodukt van twee vektoren: $$ ( \vec{a} \cdot \vec{b} )^2 \; \le \; ( \vec{a} \cdot \vec{a} ) \: ( \vec{b} \cdot \vec{b} ) $$ Kwadrateer het totale overgedragen vermogen $= a.(T_P - T_S)$ en werk uit: $$ \left[ \iiint a/(c.G_P).(T_P - T_S) \, dV \right]^2 = \left[ \iiint \left\{ u.\frac{\partial T_P}{\partial r} +v.\frac{\partial T_P}{\partial z} \right\} \, dV \right]^2 $$ $$ \leq \left[ \iiint \left\{ u^2 + v^2 \right\} \, dV \right] \: . \: \left[ \iiint \left\{ \left(\frac{\partial T_P}{\partial r} \right)^2 + \left(\frac{\partial T_P}{\partial z} \right)^2 \right\} \, dV \right] $$ Zodat: $$ \iiint \left\{ \left(\frac{\partial T_P}{\partial r} \right)^2 + \left(\frac{\partial T_P}{\partial z} \right)^2 \right\} \, dV \geq \frac{ ( \mbox{ totaal overgedragen vermogen} )^2 } { (c.G_P)^2 \, \iiint \left\{ u^2 + v^2 \right\} \, dV } $$ Uit de theoretische stromingsleer is bekend dat van alle onsamendrukbare stromingen waarbij de normale snelheidskomponent op de wanden hetzelfde is, de potentiaalstroming of ideale stroming de kleinste kinetische energie bezit. Dit betekent dat de noemer aan de rechterkant voor een ideale stroming minimaal is, de term als geheel dus maximaal, even aangenomen dat het totale overgedragen vermogen niet verandert. Aan de linkerkant staat de integrale (kwadraat)grootte van de temperatuurgradiënten. Die worden onder deze omstandigheden kennelijk maximaal berekend. Dus berekeningen die gemaakt worden met een ideale inwendige stroming als basis zijn stellig aan de veilige kant, omdat zij aanleiding geven tot overdreven temperatuurspanningen bij gegeven operationele kondities.

De natuurwetten van de warmtewisselaar kan een zekere schoonheid niet worden ontzegd. Maar eens te meer is duidelijk waar deze elegantie in wezen vandaan komt. Ze is louter en alleen het gevolg van een buitengemeen versimpelde voorstelling van zaken, inherent aan het vloeistof-pijpen continuüm model. Heel in het algemeen stellen wij:
Natuurwetten zien er alleen maar simpel en elegant uit doordat er grove vereenvoudigingen zijn toegepast.
De warmteoverdracht coëfficienten $a$ in bovenstaand stelsel vergelijkingen worden samengesteld uit een warmtedoorgangscoëfficient voor de pijpwand (die verreweg het belangrijkst is), in kombinatie met warmtedoorgangscoëfficienten natriumzijdig, aan de primaire en aan de sekundaire kant. Voor de natriumzijdige coëfficienten kan men in de litteratuur verschillende zogenaamde "correlaties" vinden. Welnu, over smaak valt niet te twisten, maar ik ben nog nooit van mijn leven zulke afschuwelijke formules tegengekomen:
Hoe "dichter" bij de werkelijkheid, des te lelijker de wiskunde lijkt het wel, in plaats van de tegenovergestelde gemeenplaats dat "fundamentele" formules per definitie ook "mooi" zouden zijn.
Alsof op een zeker punt het "genoeg" van de vereiste nauwkeurigheid is bereikt, waardoor het nut van nog langer mathematisch elegant te zijn wegvalt.

De warmteoverdracht vergelijkingen kunnen "exakt" worden geïntegreerd in het minder interessante deel van de pijpenbundel, waar de stroming parallel aan de pijpen loopt, en dus niet langer tweedimensionaal is. Voor dat gebied kan het zogenaamde éénpijpsmodel worden afgeleid, een stelsel gewone differentiaalvergelijkingen dat op de standaard manier kan worden opgelost. Het gaat hier om een bekend stuk theorie, waar wij weinig leerzaams aan kunnen toevoegen: voor geïnteresseerden is er het Eenpijpsmodel.

Behalve voor het parallelstroom gedeelte kunnen analytische oplossingen worden gevonden op enkele andere plaatsen in de warmtewisselaar. Het gemakkelijkst is zo'n oplossing te konstrueren voor de stroomlijn die loopt vanaf de verbinding van de centrale pijp met de onderste pijpplaat naar de uitstroomperforatie:

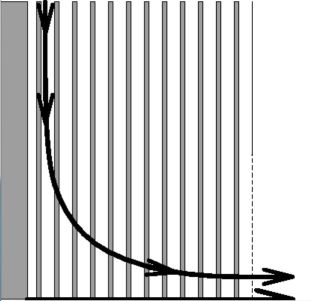
De vergelijkingen reduceren daar tot één gewone differentiaalvergelijking voor primaire temperaturen, omdat de sekundaire temperatuur randvoorwaarde is. Bovendien hebben we een uitdrukking voor de stromingsverdeling ter plaatse, volgens het TA/K model. Substitutie daarvan maakt duidelijk dat: $$ c.G_P.\frac{1}{2.F} \left( r - \frac{R^2}{r} \right) \frac{dT_P}{dr} + a.[ \, T_P - T_{S0} \, ] = 0 $$ De oplossing van zo'n gewone differentiaalvergelijking wordt routinematig gevonden met OperatorenRekening: $$ \left[ \frac{d}{dr} + \frac{2.r.F.a/(c.G_P)}{r^2 - R^2} \right] (T_P - T_{S0}) = 0 $$ We moeten integreren de term: $$ \int \frac{2.r.F.a/(c.G_P)}{r^2 - R^2} \, dr = \frac{F.a}{c.G_P} \int \frac{dr^2}{r^2 - R^2} = \frac{F.a}{c.G_P} \log \left( \frac{r^2}{R^2} -1 \right) $$ Waarmee de differentiaalvergelijking wordt omgewerkt tot: $$ \left( \frac{r^2}{R^2} -1 \right)^{ - F.a/(c.G_P) } \: \frac{d}{dr} \: \left( \frac{r^2}{R^2} -1 \right)^{ + F.a/(c.G_P) } \: (T_P - T_{S0})= 0 $$ Waarvan de oplossing is: $$ T_P - T_{S0} = K.\left( \frac{r^2}{R^2} -1 \right)^{ - H } \quad \mbox{waarin} \quad H = F.a/(c.G_P) $$ Verder is $K$ een (tamelijk) onbekende konstante. Omdat $(r^2/R^2 - 1)$ in de hoek nul kan worden, en de grootheid $-H$ een negatieve macht is, is de oplossing singulier: een zwart gat .
Maar natuurlijk niet! Oneindigheden van deze aard kunnen in een warmtewisselaar helemaal niet bestaan. We weten op fysische gronden absoluut zeker dat alle temperaturen zich bevinden tussen de grenzen $T_{S0}$, de sekundaire intree-temperatuur, en $T_{PL}$, de primaire intree-temperatuur. We moeten nu wel konkluderen dat de konstante $K$ niet anders kan zijn dan gelijk aan nul. Als gevolg hiervan geldt langs de onderste stroomlijn in het apparaat: $T_P = T_{S0}$; de primaire temperatuur is daar gelijk aan de sekundaire inlaat-temperatuur.

Nu lijkt toch sprake van overhaaste konklusies. Men worde eraan herinnerd dat het vloeistof-pijpen continuüm een ruw model is. Daarom is het verantwoord telkens vraagtekens te zetten bij de geldigheid van het model. In het bijzonder is oplettendheid geboden wanneer er singulariteiten in het model optreden. Plaatsen waar singulariteiten optreden zijn zonder meer verdacht. Oneindigheden zijn immers fysisch onbestaanbaar. Maar in plaats van al te snel te konkluderen tot een nul-oplossing, kan een singulariteit er ook simpelweg op duiden dat op zekere plaatsen de continuüm aanname niet langer opgaat. Nu zagen we dat in het continuüm model de oplossing een benadering is voor infinitesimale volumina ter grootte van de steek. Als we de oplossing middelen over een ring ter breedte van de steek, dan moet zij ongeveer hetzelfde blijven. Dit is overeenkomstig de Wazige Optiek van continuïteit. Konkretiseren we deze gedachte voor de hierboven gevonden analytische oplossing (waarbij gemakshalve wordt afgezien van het zeer speciale geval dat $H = 1$): $$ K.\frac{ \int_{x}^{x+s} \left[ \, (r/R)^2-1 \, \right]^{-H} \, 2.\pi.r.dr }{ \pi.[ \, (x+s)^2 - x^2 \, ] } = $$ $$ \frac{K}{1-H}. \frac{ \left[ \left( \frac{x+s}{R} \right)^2 - 1 \right]^{1 - H} - \left[ \left( \frac{x}{R} \right)^2 - 1 \right]^{1 - H} } { \left( \frac{x+s}{R} \right)^2 - \left( \frac{x}{R} \right)^2 } $$ Hierin is $s=$ de steek van de pijpenbundel; $H = F.a/(c.G_P)$. Er onstaat meteen een heel ander beeld. De singulariteit wordt verzwakt door haar uit te smeren over de steek. Er kunnen twee gevallen worden onderscheiden:

• $H > 1$ . Nog steeds een echte singulariteit. De konklusies over de nul-oplossing blijven geldig: $T_P = T_{S0}$.
• $H < 1$ . De singulariteit bestaat in dit geval niet langer. Konklusies over de nul-oplossing zijn mogelijk niet juist.
  De primaire temperatuur gaat niet overal tegen de sekundaire temperatuur aanliggen: $T_P \neq T_{S0}$.

We zouden de waarde $G_P$ waarvoor $c.G_P = F.a$ in zekere zin een kritische massastroom kunnen noemen. Het is een aardige exercitie om deze kritische massastroom eens uit te rekenen voor een echte warmtewisselaar. De volgende waarden hebben bij een konkreet apparaat gehoord. Ik vat zulke rekenkundige zaken graag samen in een BASIC programmaatje, dat tevens de kritische massastroom laat weten:

10 PI=4*ATN(1) : REM Trancendent getal
20 NP=846 : REM aaNtal Pijpen
30 DU=0.0210 : REM Diameter pijpen bUiten
40 DI=0.0182 : REM Diameter pijpen bInnen
50 L=20 : REM geLeidingsvermogen pijpwand
60 REM globale wArmteoverdracht-constante:
70 A=NP*2*PI*L/LOG(DU/DI)
80 F=0.370 : REM hoogte uitstroomperForatie
90 C=1275 : REM warmteCapaciteit natrium
100 REM kritische Primaire massastroom:
110 GP=F*A/C : PRINT GP