overzicht overview
Wazige Optiek [ EN ]
Mijn oudste zoon zei laatst (< 1995) tegen me: "je moet je ogen half dicht doen, dan zie
je het beter". Ik denk dat dit het wezen van de continuïteit goed weergeeft.
Tijdens de natuurkundelessen op de middelbare school werd vroeger een stukje
geometrische optika behandeld: holle en bolle spiegels en dito lenzen. Daarbij
wordt als vanzelfsprekend uitgegaan van een scherp beeld, als we praten
over de beeldafstand. Ik stel voor om deze goede gewoonte even te laten varen,
en in plaats daarvan nu eens een wazig beeld onder de loep te nemen.
In de volgende figuur zien we, sterk uitvergroot, de meetkunde van een wazige
afbeelding weergegeven:
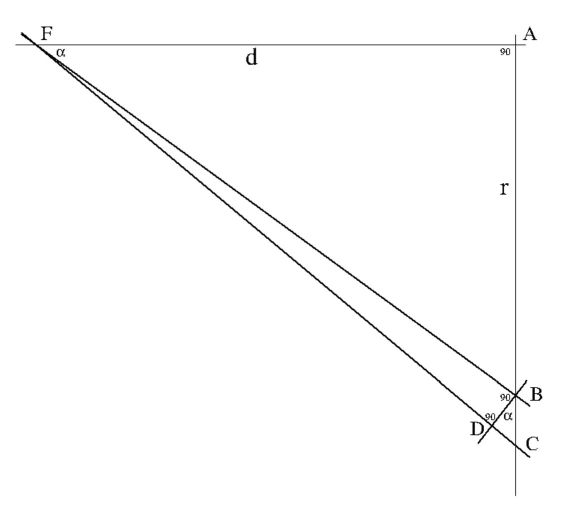
Gewoonlijk wordt een scherp beeld gevormd op de plaats $F$. Echter we gaan nu
met het vlak van beeldvorming een beetje naar rechts staan over een afstand $d$.
Beschouw een zeer smalle lichtbundel $FBC$. Deze waaiert langzaam uit en treft
het beeldvlak over een oppervlak $BC$. Omdat de lichtbundel zeer smal is, zijn
de beide hoeken $FBD$ en $FDB$ vrijwel 90 graden. Dit betekent dat hoek $CBD$
vrijwel gelijk zal zijn aan hoek $BFA$. Noem deze hoek $\alpha$. We berekenen
de lichtdichtheid $P$ op het vlakje $BC$. Neem aan dat het licht afkomstig is
van een puntvormige lichtbron die een sterkte van 1 heeft, dan is:
$P=cos(\alpha)/2\pi R^2 $(: halve bol).
Hierin is $cos(\alpha) = d/R$ en $R = \sqrt{r^2+d^2} $. Wanneer we het vlakje
$BC$ tot een punt samentrekken, dan vinden we voor de lichtsterkte ter plaatse
de volgende "exakte" uitdrukking:
$$ P(r) = \frac{d/2\pi}{(r^2+d^2)^{3/2}} $$
Merk op dat de afleiding met behulp van twee (ongeveer) rechte hoeken $FBD$ en
$FDB$ pas achteraf, bij de limietovergang, gerechtvaardigd wordt -
typisch voorbeeld van een "afleiding met pijn", zoals die in de technische
wetenschappen vaak wordt toegepast.
Merk een paar dingen op. Ten eerste dat er opnieuw een scherp beeld ontstaat
(om precies te zijn een delta-funktie) zodra de afstand $d$ nadert tot nul.
Integratie van de gevonden formule over het hele beeldvlak moet uiteraard een
totale lichtopbrengst van $1$ geven. We kunnen dit kontroleren:
$$ \iint \frac{d/2\pi}{(r^2+d^2)^{3/2}} \, r.dr.d\phi =
2\pi.\frac{1}{2\pi}.\int_0^\infty \!
\frac {r/d.d(r/d)} {\left[(r/d)^2+1\right]^{3/2} } =
- \frac{2}{2}.\left[x^{-1/2}\right]_1^\infty = 1 $$
Nemen we in plaats van de puntvormige lichtbron een lijn, dan moet de funktie
$P$ langs die lijn worden geïntegreerd. Langs de lijn wordt gemeten met een
lengte $l$. De straal $r$ in bovenstaande formules is dan gelijk aan $p^2+l^2$,
waarin $p$ de afstand van een punt $(x,y)$ tot de lijn is. De integratie loopt
dan als volgt:
$$ L = \int_{-\infty}^{+\infty} \! \frac{d/2\pi}{(p^2+l^2+d^2)^{3/2}} \, dl =
\frac{d/2\pi}{p^2+d^2} \int_{-\infty}^{+\infty} \!
\frac{ d\left( \frac{l}{\sqrt{p^2+d^2}} \right) }
{ \left[ 1 + \left( \frac{l}{\sqrt{p^2+d^2}} \right)^2 \right]^{3/2} } $$
$$ = \frac{d/2\pi}{p^2+d^2}
\left[ \frac{x}{(1+x^2)^{1/2}} \right]_{-\infty}^{+\infty}
= \frac{d/2\pi}{p^2+d^2} . 2 $$
Wanneer de vergelijking van de lijn gegeven is door $ ax + by + c = 0 $ , dan
wordt de afstand van een punt $(x,y)$ tot de lijn middels een bekende formule
gegeven door $ p = (ax + by + c)/\sqrt(a^2+b^2) $ . Hiermee is de lichtsterkte
verdeling van een wazige afbeelding van een lijn:
$$ L(x,y) = \frac{d/\pi}{(ax+by+c)^2/(a^2+b^2)+d^2} $$
Dit is een funktie die in de statistiek bekend staat als een Cauchy verdeling.
Ook nu wordt voor $d \rightarrow 0$ weer een scherp plaatje verkregen, en is de
integrale lichtsterkte gelijk aan $1$.
In het algemeen kunnen we een scherpe figuur omzetten in een wazige afbeelding
op de volgende manier. Stel dat we van een "punt" de wazige afbeelding kennen.
We noemen deze "eenheids" afbeelding: $h(x)$. Maar iedere scherpe figuur wordt
natuurlijk punt voor punt afgebeeld. Noem de scherpe figuur $f(x)$, dan is de
lichtsterkte van alleen de funktiewaarde $f(x)$ ter plaatse $\xi$ gelijk aan
$f(\xi)h(x-\xi)$. Dit moeten we vervolgens integreren over het hele beeldvlak,
om de wazige afbeelding $F$ van $f$ te krijgen:
$$ F(x) = \int_{-\infty}^{+\infty} \! f(\xi)h(x-\xi) \, d\xi
= \int_{-\infty}^{+\infty} \! h(\xi)f(x-\xi) \, d\xi $$
Deze uitdrukking staat bekend als een convolutie integraal. De afleiding
werd gegeven voor het ééndimensionale geval, maar het idee gaat natuurlijk
net zo goed op voor de twee dimensies van het beeldvlak.
Beelden we bijvoorbeeld in plaats van de lijn een lichtend halfvlak wazig af.
Het scherpe beeld is in dit geval een Heaviside of sprong funktie $H(p)$. Dan
is met behulp van het bovenstaande:
$$ V = \int_{-\infty}^{+\infty} \! \frac{d/\pi}{\xi^2+d^2} H(p-\xi) \, d\xi =
\frac{1}{\pi} \int_{-\infty}^{p} \! \frac{d \left( \frac{\xi}{d} \right) }
{ \left[ 1 + \left( \frac{\xi}{d} \right)^2 \right] } \, d\xi =
\frac{1}{\pi} arctan( \frac{p}{d} ) + \frac{1}{2} $$
$$ = \frac{1}{\pi} arctan(\frac{ax+by+c}{d \sqrt{a^2+b^2}}) + \frac{1}{2} $$
Wederom wordt voor $d \rightarrow 0$ een scherp plaatje $H(p)$ verkregen.
Anders dan de titel van dit hoofdstuk deed vermoeden, is het maken van wazige
afbeeldingen exakt te beschrijven, met middelen van de klassieke analyse.
Niet voor niets zijn we ons te buiten gegaan aan een overdaad van mathematische
formules. Er is strikt genomen niets wazigs aan het idee van een wazige optiek.
