Inverse Fourier transform method
$
\def \sinc {\operatorname{sinc}}
\def \slechts {\quad \Longleftrightarrow \quad}
\def \half {\frac{1}{2}}
$
We have found that the Fourier transform of a block function is a $\,\sinc\,$ and
the Fourier transform of a $\,\sinc\,$ is a block function. This is, of course,
no coincidence. Hat functions are symmetric, therefore the Fourier integral and
the inverse thereof are:
$$
\int_{-\infty}^{+\infty} p(x) \cos(y x) \,dx = A(y) \slechts
\frac{1}{2\pi} \int_{-\infty}^{+\infty} A(y) \cos(x y) \,dy = p(x)
$$
So if the Fourier integral of a hat function $\,p(x)\,$ is $\,A(y)\,$, then the Fourier
integral of the hat function $\,A(x)\,$ is $\,2\pi\,p(y)\,$. Let's check it at hand of
functions in previous subsections:
$$
p(x) = \frac{1}{\sigma} \sinc\left(\frac{\pi}{\sigma} x\right) \slechts
A(y) = \left\{ \begin{array}{lll}
0 & \mbox{for} & y < -\pi/\sigma \\
1 & \mbox{for} & -\pi/\sigma < y < +\pi/\sigma \\
0 & \mbox{for} & +\pi/\sigma < y
\end{array} \right.
$$ $$
p(x) = \left\{ \begin{array}{lll}
0 & \mbox{for} & x \le -\half \sigma \\
1/\sigma & \mbox{for} & -\half\sigma \le x \le +\half\sigma \\
0 & \mbox{for} & +\half \sigma \le x
\end{array} \right. \slechts
A(y) = \sinc(\half y \sigma)
$$
Modify the latter formulas by the method of careful substitution. Three steps
can be distinguished in this procedure: (1) adjust proper spread, (2) adjust
proper norm, (3) what's in a name? Okay, let's just do it. Start with adjusting
proper spread and let $\,\sigma/2 \rightarrow \pi/\sigma\,$:
$$
p(x) = \left\{ \begin{array}{lll}
0 & \mbox{for} & x \le -\pi/\sigma \\
\sigma/(2\pi) & \mbox{for} & -\pi/\sigma \le x \le +\pi/\sigma \\
0 & \mbox{for} & +\pi/\sigma \le x
\end{array} \right. \slechts
A(y) = \sinc(y \pi/\sigma)
$$
Now adjust proper norm by multipling both right hand sides with $\,2\pi/\sigma\,$:
$$
p(x) = \left\{ \begin{array}{lll}
0 & \mbox{for} & x \le -\pi/\sigma \\
1 & \mbox{for} & -\pi/\sigma \le x \le +\pi/\sigma \\
0 & \mbox{for} & +\pi/\sigma \le x
\end{array} \right. \slechts
A(y) = 2\pi \times \frac{1}{\sigma} \sinc(y \pi/\sigma)
$$
At last, what's in a name? By $\,x \leftrightarrow y\,$ and $\,p \leftrightarrow A\,$,
where, according to the inverse Fourier transform method, the factor $(2\pi)$
must be discarded:
$$
p(x) = \frac{1}{\sigma} \sinc\left(\frac{\pi}{\sigma} x\right) \slechts
A(y) = \left\{ \begin{array}{lll}
0 & \mbox{for} & y < -\pi/\sigma \\
1 & \mbox{for} & -\pi/\sigma < y < +\pi/\sigma \\
0 & \mbox{for} & +\pi/\sigma < y
\end{array} \right.
$$
Quod Erat Demonstrandum / Quite Easily Done.
Slightly more interesting is to
apply the method for obtaining a new result, instead of reproducing an old one.
Copy and paste from the subsection Comb of Triangles:
$$
p(x) = \left\{ \begin{array}{lll}
0 & \mbox{for} & x \le -\sigma \\
(\sigma+x)/\sigma^2 & \mbox{for} & -\sigma \le x \le 0 \\
(\sigma-x)/\sigma^2 & \mbox{for} & 0 \le x \le +\sigma \\
0 & \mbox{for} & +\sigma \le x
\end{array} \right. \slechts
A(y) = \sinc^2(\half y \sigma)
$$
Modify the latter formulas by the method of careful substitution. Adjust proper
spread first and let $\,\sigma/2 \rightarrow \pi/\sigma\,$ again:
$$
p(x) = \frac{\sigma}{2\pi} \left\{ \begin{array}{lll}
0 & \mbox{for} & x \le -2\pi/\sigma \\
1+x \sigma/(2\pi) & \mbox{for} & -2\pi/\sigma \le x \le 0 \\
1-x \sigma/(2\pi) & \mbox{for} & 0 \le x \le +2\pi/\sigma \\
0 & \mbox{for} & +2\pi/\sigma \le x
\end{array} \right. \slechts
A(y) = \sinc^2(y \pi/\sigma)
$$
Now adjust proper norm by multipling both right hand sides with $\,2\pi/\sigma\,$:
$$
p(x) = \left\{ \begin{array}{lll}
0 & \mbox{for} & x \le -2\pi/\sigma \\
1+x\sigma/(2\pi) & \mbox{for} & -2\pi/\sigma \le x \le 0 \\
1-x\sigma/(2\pi) & \mbox{for} & 0 \le x \le +2\pi/\sigma \\
0 & \mbox{for} & +2\pi/\sigma \le x
\end{array} \right.
\slechts A(y) = \frac{2\pi}{\sigma}\sinc^2(y \pi/\sigma)
$$
Now in the space domain $\,p(0) = 1\,$, which is the same as, in the Fourier domain:
$$
\frac{2\pi}{\sigma} \int_{-\infty}^{+\infty} \sinc^2(y \pi/\sigma) \, dy =
2\, \int_{-\infty}^{+\infty} \sinc^2(y \pi/\sigma) \, d(y \pi/\sigma) =
2\,\pi
$$
At last, what's in a name? By $\,x \leftrightarrow y\,$ and $\,p \leftrightarrow A\,$,
where, according to the inverse Fourier transform method, the factor $(2\pi)$
must be discarded:
$$
p(x) = \frac{1}{\sigma}
\left[\frac{\sin(\pi/\sigma\, .\,x)}{\pi/\sigma\, .\,x}\right]^2
= \frac{1}{\sigma} \sinc^2\left(\frac{\pi}{\sigma} x\right)
$$ $$
\slechts A(y) = \left\{ \begin{array}{lll}
0 & \mbox{for} & y \le -2\pi/\sigma \\
1+y\sigma/(2\pi) & \mbox{for} & -2\pi/\sigma \le y \le 0 \\
1-y\sigma/(2\pi) & \mbox{for} & 0 \le y \le +2\pi/\sigma \\
0 & \mbox{for} & +2\pi/\sigma \le y
\end{array} \right.
$$
Resulting in a Comb of Squared Sinc functions that we haven't seen before:
$$
\frac{\Delta}{\sigma} \sum_{L=-\infty}^{+\infty}
\sinc^2\left(\frac{\pi}{\sigma}\left[x-L\Delta\right]\right) =
1 + \sum_{k=1}^\infty A(k\omega\sigma)\,\cos(k\omega x)
$$
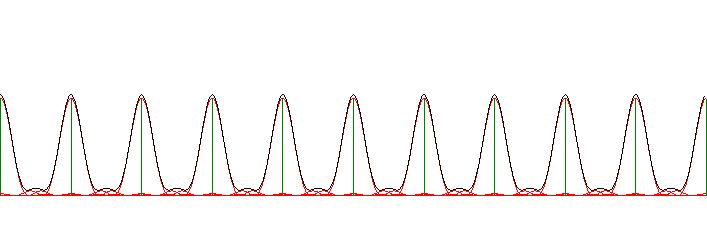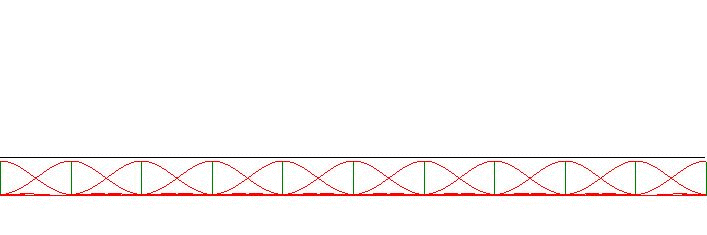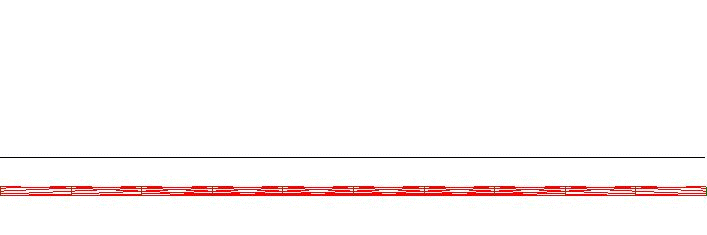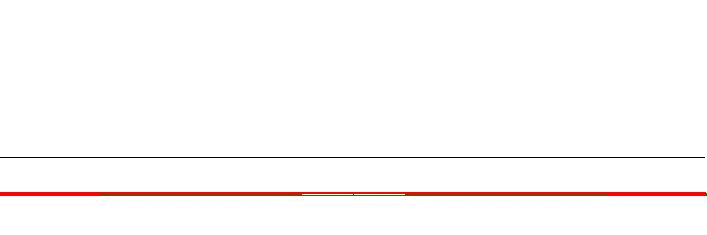
So what we have now is the rectangle and the sinc function, the triangle and
the sinc squared function. We also have a Cauchy distribution and exponential
decay:
$$
p(x) = \frac{\sigma/\pi}{\sigma^2 + x^2} \slechts A(y) = e^{-|y|\sigma}
$$
The absolute value is needed because we must have a hat shape and at the
same time prevent an explosion for negative $\,y\,$. The other way around; adjust
proper spread first. For an exponential decay that is $\,\exp(-|y|/\sigma)\,$,
where $\,\sigma\,$ is the decay rate. Therefore substitute $\,\sigma \rightarrow
1/\sigma\,$, resulting in:
$$
p(x) = \frac{\sigma/\pi}{1 + (x\sigma)^2} \slechts A(y) = e^{-|y|/\sigma}
$$
Now adjust proper norm by multipling both right hand sides with $\,\pi/\sigma\,$:
$$
p(x) = \frac{1}{1 + (x\sigma)^2} \slechts
A(y) = 2\pi \times \frac{e^{-|y|/\sigma}}{2\sigma}
$$
At last, what's in a name? By $\,x \leftrightarrow y\,$ and $\,p \leftrightarrow A\,$,
where, according to the inverse Fourier transform method, the factor $(2\pi)$
must be discarded:
$$
p(x) = \frac{e^{-|x|/\sigma}}{2\sigma} \slechts
A(y) = \frac{1}{1 + (y\sigma)^2}
$$
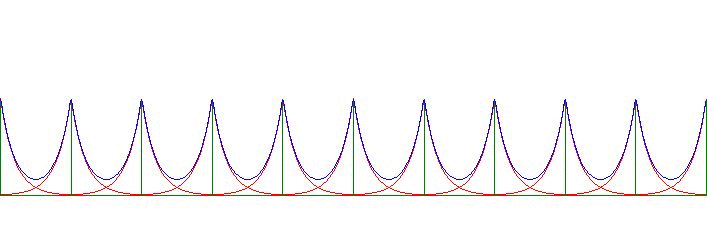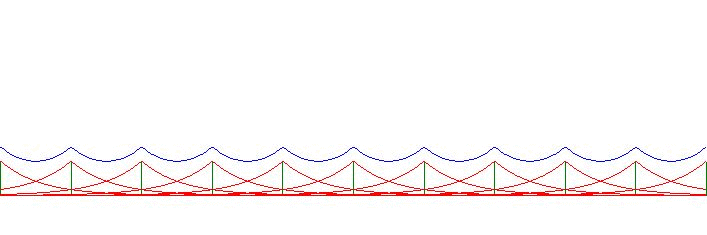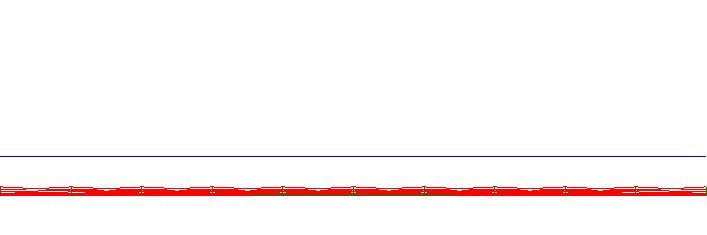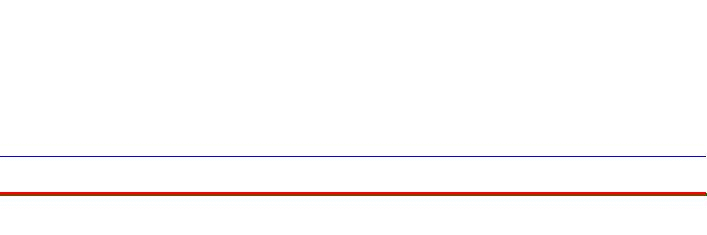
Resulting in a Comb of Exponential Decays that we haven't seen before:
$$
\frac{\Delta}{2\sigma} \sum_{L=-\infty}^{+\infty} e^{-|x-L\Delta|/\sigma} =
1 + \sum_{k=1}^\infty \frac{\cos(k\omega x)}{1 + (k\omega\sigma)^2}
$$
There are a hundred ways to Rome, though. We could have found this result in a
far more direct way with integrals from the subsection Find more Fourier integrals.
Working the other way around - that is: starting with exponential decays
and with the inverse Fourier transform method find the Cauchy distribution - we
could have avoided the complex analysis solution employed in the subsection
Comb of Cauchy Distributions.
Last but not least, here is our beloved Gaussian:
$$
p(x) = \frac{1}{\sigma\sqrt{2\pi}}\, e^{-\half (x/\sigma)^2} \slechts
A(y) = e^{-\half (y\sigma)^2}
$$
Proper spread with $\,\sigma \rightarrow 1/\sigma\,$:
$$
p(x) = \frac{\sigma}{\sqrt{2\pi}}\, e^{-\half (x\sigma)^2} \slechts
A(y) = e^{-\half (y/\sigma)^2}
$$
Proper norm with times $\,\sqrt(2\pi)/\sigma\,$:
$$
p(x) = e^{-\half (x\sigma)^2} \slechts
A(y) = \frac{\sqrt{2\pi}}{\sigma}\, e^{-\half (y/\sigma)^2}
= 2\pi \times \frac{1}{\sigma\sqrt{2\pi}}\, e^{-\half (y/\sigma)^2}
$$
At last, what's in a name? By $\,x \leftrightarrow y\,$ and $\,p \leftrightarrow A\,$,
where, according to the inverse Fourier transform method, the factor $(2\pi)$
must be discarded:
$$
p(x) = \frac{1}{\sigma\sqrt{2\pi}}\, e^{-\half (x/\sigma)^2} \slechts
A(y) = e^{-\half (y\sigma)^2}
$$
Herewith, everything considered so far has been covered:
Gaussian $\leftrightarrow$ itself, Cauchy $\leftrightarrow$ Decay,
Block $\leftrightarrow$ Shannon, Triangle $\leftrightarrow$ Squared.


