Comb of Cauchy Distributions
$
\def \MET {\qquad \mbox{where} \quad}
\def \hieruit {\quad \Longrightarrow \quad}
\def \slechts {\quad \Longleftrightarrow \quad}
$
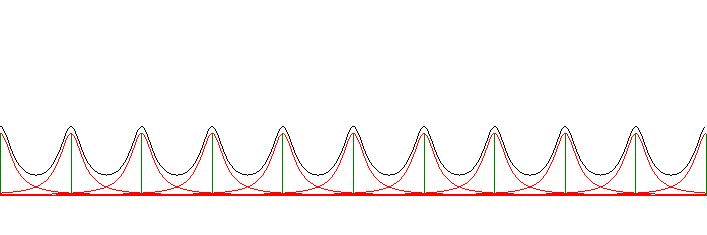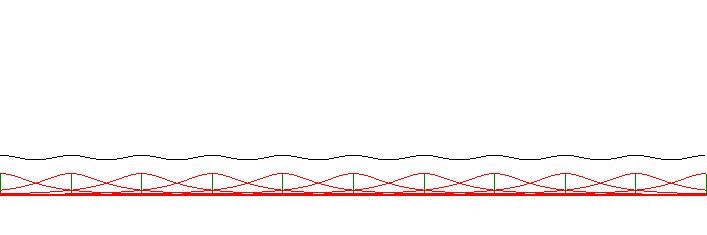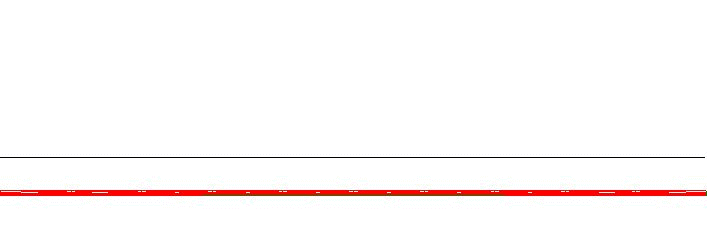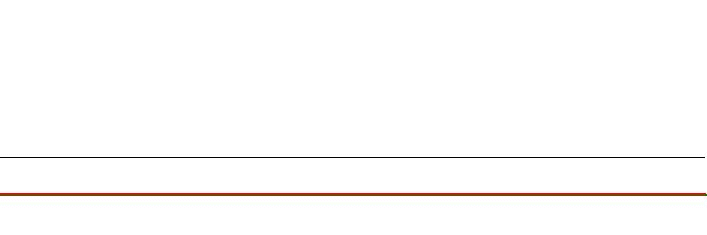
The subject of our current study is a comb $\,P(x)\,$ of normed Cauchy distributions
$\,p(x)\,$ at a one dimensional, infinite and equidistant grid
with discretization $\,\Delta\,$, embedded on the real axis
with coordinate $x$ :
$$
P(x) = \sum_{L=-\infty}^{+\infty} p(x-L.\Delta)\,\Delta
\MET p(x) = \frac{\sigma/\pi}{\sigma^2+x^2}
$$
The function $P(x)$ can be interpreted as an attempt to "smooth" the uniform
density $x_L = L.\Delta$. Or "make fuzzy" the discretization $f(x_L) = 1$ of
a constant - and continuous - function $f(x) = 1$.
Check that $p(x)$ is indeed normed:
$$
\int_{-\infty}^{+\infty} \frac{\sigma/\pi}{\sigma^2+x^2}\,dx =
\int_{-\infty}^{+\infty} \frac{1/\pi}{1+(x/\sigma)^2}\,d(x/\sigma) =
\frac{1}{\pi} \int_{-\infty}^{+\infty} \frac{dt}{1+t^2} =
$$ $$
\frac{1}{\pi} \left[ \arctan(t) \right]_{-\infty}^{+\infty} = \pi/\pi = 1
$$
The spread $\sigma$ of a Cauchy distribution, despite of its name, is not
a standard deviation, as is clear from the following, with help of the above:
$$
\int_{-\infty}^{+\infty} \frac{\sigma/\pi}{\sigma^2+x^2}\,x^2\,dx
= \frac{\sigma}{\pi} \int_{-\infty}^{+\infty}
\frac{\sigma^2+x^2}{\sigma^2+x^2}\, dx
- \sigma^2 \int_{-\infty}^{+\infty} \frac{\sigma/\pi}{\sigma^2+x^2}\,dx
$$ $$
= \frac{\sigma}{\pi} \left[ x \right]_{-\infty}^{+\infty} - \sigma^2\, .\, 1
= \frac{\sigma}{\pi} \, 2 \: \infty - \sigma^2 = \infty
$$
Nothing can remove this infinite outcome for the standard deviation of a Cauchy
distribution. The Fourier series for a comb of Cauchy distributions is:
$$
P(x) = 1 + 2 \times \sum_{k = 1}^{\infty} A(k \omega) \, \cos(k \omega x)
$$
Where it is reminded that $\omega = 2\pi / \Delta$. And:
$$
A(y) = \int_{- \infty}^{+ \infty} p(x) \cos(y x) \, dx
= \frac{\sigma}{\pi} \int_{- \infty}^{+ \infty}
\frac{\cos(y x)}{\sigma^2 + x^2} \, dx
$$
Complex Analysis is required in order to solve for this integral.
A full outcome can be found in the (Dutch) book
[ S.T.M Ackermans & J.H. van Lint, algebra en analyse,
Academic Service, Den Haag (1976) ]. On page 458 we read:

Conclusion:
$$
\int_0^{\infty} \frac{\cos(x)}{a^2+x^2} dx = \frac{\pi e^{-a}}{2 a}
$$
In concordance with this, we shall rewrite the expression for $A(y)$ a little
bit:
$$
A(y) = \frac{\sigma}{\pi} \int_{- \infty}^{+ \infty}
\frac{\cos(y x)y}{y^2( \sigma^2 + x^2)} \, d(yx)
= \frac{y \sigma}{\pi} \int_{- \infty}^{+ \infty}
\frac{\cos(x)}{(y \sigma)^2 + x^2} \, dx
$$ $$
= \frac{a}{\pi} 2 \int_0^{+ \infty}
\frac{\cos(x)}{a^2 + x^2} \, dx
= \frac{a}{\pi} \, 2 \, \frac{\pi e^{-a}}{2 a} = e^{-a}
$$
Where $a = y \sigma$, resulting in an extremely simple outcome for the
coefficients: $A(y) = e^{-y \sigma}$.
We conclude that the Fourier series of a Uniform Comb of Cauchy distributions
is given by:
$$
P(x) = \sum_{L = -\infty}^{+\infty} p(x - L \Delta)\,\Delta =
1 + 2 \times \sum_{k = 1}^{\infty} e^{-k\omega\sigma}\,\cos(k\omega x)
$$
Where it is reminded that: $\omega = 2 \pi / \Delta$.
It is seen that $P(x)$ is approximately equal to $1$, provided that the rest
of the Fourier series expansion is sufficiently small. First we take, out of
thin air, an "acceptable" (relative) error $0 < \epsilon < 1$.
As a next step, the following requirement is imposed.
$$
\left| 2 \times \sum_{k = 1}^{\infty} e^{-k\omega\sigma}\,\cos(k\omega x)
\right| < \epsilon
$$
Because the cosine is in between $-1$ and $+1$, it is furthermore evident that
a sufficient condition for the above is:
$$
\sum_{k = 1}^{\infty} e^{-k\omega\sigma} < \epsilon/2
$$
A geometric series is recognized herein:
$$
e^{-\omega\sigma} \sum_{k = 0}^{\infty} \left( e^{-\omega\sigma} \right)^k
< \epsilon/2 \slechts \frac{e^{-\omega\sigma}}{1-e^{-\omega\sigma}}
< \epsilon/2
$$ $$
\slechts e^{-\omega\sigma} < \frac{\epsilon/2}{1+\epsilon/2}
\slechts \sigma > \frac{\Delta}{2\pi}
\ln\left(\frac{1+\epsilon/2}{\epsilon/2} \right)
$$
A quantity called $\alpha$ (alpha) for the Cauchy distribution is defined as:
$$
\alpha = \ln\left(1+\frac{2}{\epsilon}\right)
\approx \ln(2/\epsilon) \hieruit \sigma > \frac{\Delta}{2\pi}\alpha
$$
The latter approximation because errors are supposed to be small. It is noticed
that the approximation can also be obtained by considering only the second
term of the Fourier expansion instead of the whole rest of the series.
It is concluded that $\alpha$ is varying less slowly when compared with
the analogous quantity for Gauss distributions, which has been found before as
$\alpha = \sqrt{2\:\ln(2/\epsilon)}$ in Uniform Comb of
Gaussians.

