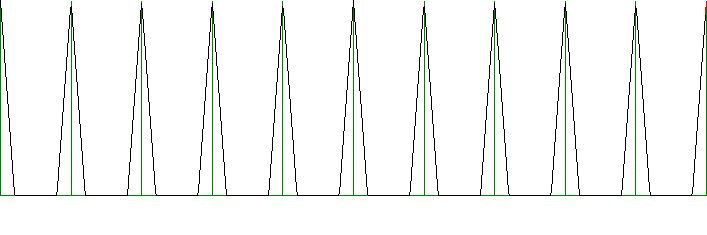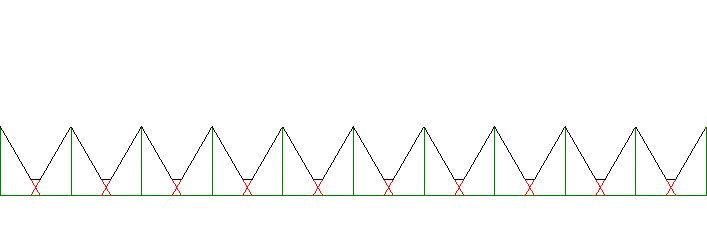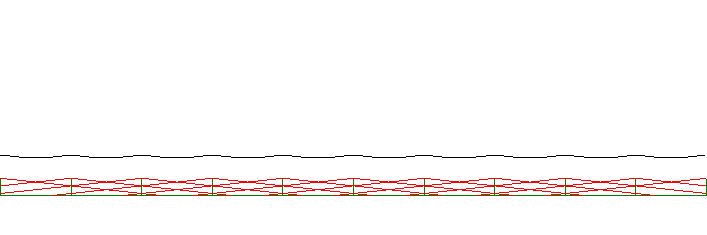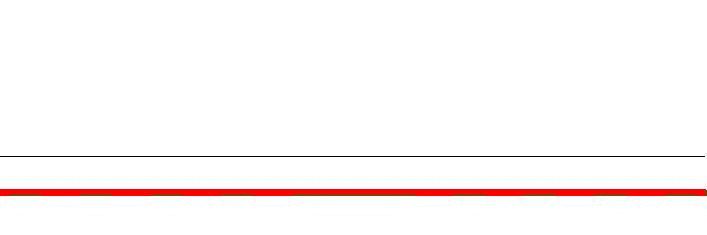
The subject of our current study is a Comb $P(x)$ of triangular distributions $p(x)$ at some uniform grid with discretization $L.\Delta$: $$ P(x) = \sum_{L=-\infty}^{+\infty} p(x-L.\Delta) \, \Delta $$ $$ \MET p(x) = \left\{ \begin{array}{lll} 0 & \mbox{for} & x \le -\sigma \\ (\sigma+x)/\sigma^2 & \mbox{for} & -\sigma \le x \le 0 \\ (\sigma-x)/\sigma^2 & \mbox{for} & 0 \le x \le +\sigma \\ 0 & \mbox{for} & +\sigma \le x \end{array} \right. $$ The geometrical picture is a triangle with base $2\sigma$ and height $1/\sigma$, resulting in an area $1$, thus establishing that the function $p(x)$ is normed. The spread $\sigma > 0$ of a triangular distribution, despite of its name, is not exactly a standard deviation, as is clear from the following: $$ \int_{-\infty}^{+\infty} x^2 p(x) \, dx = \int_{-\sigma}^0 x^2 \frac{\sigma+x}{\sigma^2} \, dx + \int_0^{+\sigma} x^2 \frac{\sigma-x}{\sigma^2} \, dx = $$ $$ \left[ \frac{x^3}{3\sigma} + \frac{x^4}{4\sigma^2} \right]_{-\sigma}^0 + \left[ \frac{x^3}{3\sigma} - \frac{x^4}{4\sigma^2} \right]_0^{+\sigma} = \sigma^2/3 - \sigma^2/4 + \sigma^2/3 - \sigma^2/4 = \sigma^2/6 $$ $$ \hieruit \mbox{standard deviation} = \sigma / \sqrt{6} $$ $P(x)$ is developed into the standard Fourier series for combs of hat functions: $$ P(x) = 1 + 2 \times \sum_{k = 1}^{\infty} A(k \omega) \, cos(k \omega x) \MET A(y) = \int_{-\infty}^{+\infty} p(x) \cos(x y) \, dx $$ With a little help from MAPLE - could have done this by hand, but I'm lazy:
int((sigma+x)/sigma^2*cos(y*x),x=-sigma..0) + int((sigma-x)/sigma^2*cos(y*x),x=0..+sigma);Giving: $$ -\frac{2(-1+cos(\sigma y))}{\sigma^2 y^2} $$ To be converted into a slightly different expression with $\cos(2x) = 1 - 2\sin^2(x)$: $$ -2 \frac{-1+\cos(y \sigma)}{y^2\sigma^2} = \frac{\sin^2(\half y \sigma)}{(\half y \sigma)^2} \hieruit $$ $$ P(x) = 1 + 2 \times \sum_{k=1}^\infty \left[\frac{\sin(\half k\omega\sigma)}{\half k\omega\sigma}\right]^2 \cos(k\omega x) \MET \omega = \frac{2\pi}{\Delta} $$ The Fourier analysis of a comb of Triangles is somewhat deviant from the Fourier analysis of a comb of Gaussians or Cauchy distributions. For $\sigma = m\Delta$, with $m > 0$ integer, the outcome is simply $P(x) = 1$, without any wiggles or giggles. On the other hand, especially for $\sigma = (m + \half) \Delta$, it's much harder to get rid of those wiggles. Proceeding as usual: $$ \sum_{k=1}^\infty \left[\frac{\sin(\half k\omega\sigma)}{\half k\omega\sigma}\right]^2 \le \sum_{k=1}^\infty \left[\frac{1}{\half k\omega\sigma}\right]^2 < \epsilon/2 \hieruit \frac{1}{(\half\omega\sigma)^2} \sum_{k=1}^\infty \frac{1}{k^2} < \epsilon/2 $$ Calculations can proceed because of a well known sum: $$ \sum_{k=1}^\infty\frac{1}{k^2} = \frac{\pi^2}{6} = \zeta(2) \hieruit \frac{\Delta^2}{\pi^2\sigma^2}\frac{\pi^2}{6} < \epsilon/2 \hieruit \frac{\Delta^2}{\sigma^2} < 3\,\epsilon $$ $$ \hieruit \sigma = \frac{\Delta}{\sqrt{3\,\epsilon}} \qquad \OF \qquad \sigma = \frac{\Delta}{2\pi}\, \alpha \MET \alpha = \frac{2\pi}{\sqrt{3\,\epsilon}} $$ Let's try the "improved" error analysis: $$ \frac{1}{(\half\omega\sigma)^4} \sum_{k=1}^\infty \frac{1}{k^4} < ( \epsilon/2 )^2 $$ Calculations can proceed because of a well known sum: $$ \sum_{k=1}^\infty\frac{1}{k^4} = \frac{\pi^4}{90} = \zeta(4) \hieruit \frac{\Delta^4}{\pi^4\sigma^4}\frac{\pi^4}{90} < (\epsilon/2)^2 \hieruit \frac{\Delta^4}{\sigma^4} < 90/4 \,\epsilon^2 $$ Conclusion: $$ \sigma > \frac{\Delta}{\sqrt{\epsilon \sqrt{45/2}}} \approx 0,45915 \frac{\Delta}{\sqrt{\epsilon}} \qquad \OF \qquad \sigma > \frac{\Delta}{\sqrt{3\,\epsilon}} \approx 0,57735 \frac{\Delta}{\sqrt{\epsilon}} $$ After all, it's only a matter of error estimates, no more, no less.