index $ \def \MET {\quad \mbox{with} \quad} \def \SP {\quad \mbox{;} \quad} \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} \def \EN {\quad \mbox{and} \quad} \def \OF {\quad \mbox{or} \quad} \def \half {\frac{1}{2}} $
One clue is in the fact that our opponent does not accept the difference between orbital clocks and atomic clocks. He thinks that orbital clocks simply can be dismissed as being old-fashioned. Quote mining: Orbital time is no longer used in metrology, time is always based on atomic clocks [ .. ] so it is irrelevant. No, on the contrary, it's highly relevant! Orbital mechanics (according to Newton) has its playground in orbital time, not in atomic time. One cannot dismiss an essential part of our theory without running into big problems. So let's finally reveal part of the solution. According to Milne's Formula we have, with $t=$ atomic time, $T=$ orbital time, $A=$ age, subscript $0=$ here and now: $$ t-t_0 = (T_0-A)\ln\left(\frac{T-A}{T_0-A}\right) $$ The mathematics is often smarter than the interpretation of it. It is easily seen that our so-called Age has only a meaning in orbital time. In atomic time, the corresponding "age" is minus infinity. Therefore (example given = e.g.) an electron created at $\,A\,$ has "existed forever" in atomic time. If an electron is created in atomic time instead, as is the case in the red colored argumentation in VPM debunked?, then UAC theory is simply not applicable.
Still feeling uncomfortable with the above argument? According to Milne's Formula we have: $$ t-t_0 = (T_0-A)\ln\left(\frac{T-A}{T_0-A}\right) = (T_0-A)\ln\left(1+\frac{T-T_0}{T_0-A}\right) $$ Assuming that the here and now synchronization timestamp is at $\,t_0=T_0=0\,$, the following substitutions can be made: $$ (t-t_0) \to t \SP (T_0-A) \to A \SP (T-T_0) \to T $$ The first term of a series expansion for $\,x=T/A\,$ is calculated, for small timelapses $\,t_2-t_1\,$ in atomic and in $\,T=$ orbital time. $$ t = A\ln\left(1+\frac{T}{A}\right) \hieruit \frac{dt}{dA} = \ln(1+T/A) - \frac{T/A}{1+T/A} \\ x = \frac{T}{A} \hieruit \frac{dt}{dA} = \ln(1+x)-\frac{x}{1+x} \approx \frac{1}{2}x^2 \hieruit \\ \frac{dt}{dA} \approx \frac{1}{2}\left(\frac{T}{A}\right)^2 $$ The above is only valid if the difference $\,dA\,$ between two creation timestamps may be considered as infinitesimally small. But suppose that the latter is not the case, then we have: $$ t_2-t_1 = A_2\ln\left(1+\frac{T}{A_2}\right) - A_1\ln\left(1+\frac{T}{A_1}\right) \\ \approx A_2\left[\frac{T}{A_2} - \half\left(\frac{T}{A_2}\right)^2\right] - A_1\left[\frac{T}{A_1} - \half\left(\frac{T}{A_1}\right)^2\right] = \half T^2\left(\frac{1}{A_1}-\frac{1}{A_2}\right) \hieruit \\ \frac{t_2-t_1}{A_2-A_1} \approx \half\left(\frac{T}{\sqrt{A_1A_2}}\right)^2 $$ where $\,A=\sqrt{A_1 A_2}\,$ is the geometric mean of $A_1$ and $A_2$. Similarity between the finite difference and the infinitesimal expression is now obvious. Depending on order of magnitudes, both may be useful. Furthermore, it is important to observe that under earthly conditions - that is: near the synchronization timestamp $0$ - both time scales $\,t\,$ and $\,T\,$ are nearly infinitesimal. Meaning that orbital time $\,T\,$ = atomic time $\,t\,$ as long as we are talking about seconds, minutes, hours, days, years. Now we are in the position to lay a connection with the accuracy of Atomic clocks which will be called the error $\,\delta\,$. This is a relative error, valid for just one second. Therefore, after some time $\,T\,$, we shall have $\,t_2-t_1=\delta\,T\,$ as an absolute error. For the infinitesimal case as well as for the finite difference case there is an orbital/atomic timespan $\,T\,$ needed in order to observe different ages of electrons. And the (absolute) error must be less than the difference revealed by the two observations. $$ \delta\,T \lt \frac{1}{2}\frac{T^2}{A^2} \Delta A \hieruit \delta \lt \frac{1}{2}\frac{T}{A^2} \Delta A \\ \delta\,T \lt \frac{1}{2}\frac{T^2}{A_1A_2} (A_2-A_1) \hieruit \delta \lt \frac{1}{2}\frac{T}{A_1A_2}(A_2-A_1) $$ It will be demonstrated now that Atomic time is extremely insensitive to small differences $\,\Delta A\,$ in Orbital creation timestamps. The first of the equations will be employed to obtain an estimate of $\,\delta\,$, the accuracy of our clock, needed for earthly circumstances. Let it run for, say, $\,T=$ one year. Suppose two electrons that were created at the Big Bang less than four seconds apart in orbital time. Our opponent has claimed that this time difference shall be observable with modern atomic (quantum) clocks having an accuracy of $\,\delta=10^{-18}\,$. A simple calculation (with MAPLE 8) tells us another story, however.
# Seconds in a year:
year := 31556926;
# Age of Big Bang universe
A := 13.7*10^9*year;
# Suppose two electrons that were created at A
# less than four seconds apart in orbital time
dA := 4;
# Let two Atomic clocks run for one year
# independently of each other to observe it
T := year;
# Relative error of clock required
delta := T/A^2*dA/2;
-27
delta := 0.3376713156 10
It is clear that even making the timelapse a thousand times larger will not improve the result significantly.
The relative error in atomic clocks which is required to observe that two electrons were created less than four seconds apart
in orbital time must be less than $3.3\times 10^{-26}$. Most probably such an incredible accuracy will never be achieved.
The reason is that there exists a natural bound on what can be accomplished with atomic clock time measurement: the Compton time.
It can be derived from the Compton wavelength of an electron:
# Planck's constant:
h := 6.62607015*10^(-34);
# Speed of light:
c := 299792458;
# Electron (rest) mass:
m_e := 9.1093837015*10^(-31);
# Compton time:
h/(m_e*c^2);
-20
0.8093299794 10
The Limited Validity of Special Relativity has led us to
conclude that: It is impossible to synchronize clocks within intervals smaller than the Compton time $\approx 8\times 10^{-21}\;s$.

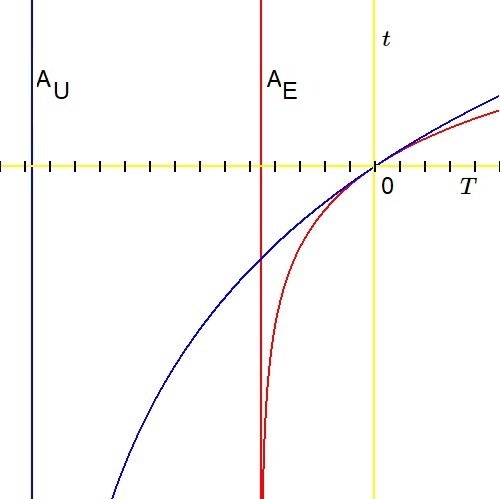
Ready for some good news? Let us compare an electron created at the supposed Big Bang $(A_U)$ with an electron having the age of the earth $(A_E)$; both are in orbital time. The graph of Milne's Formula corresponding with $A_U$ is colored blue and the graph of Milne's Formula corresponding with $A_E$ is colored red. The two asymptotes at $\,\color{blue}{T=-A_U}\,$ and $\,\color{red}{T=-A_E}\,$ are displayed as well. The black ticks at the $T$-axis are each a billion years apart. According to the above we have: $$ \delta \lt \frac{1}{2}\frac{T}{A_1A_2}(A_2-A_1) \hieruit T \gt \frac{2A_UA_E\,\delta}{A_U-A_E} $$ That's enough information again for a decent calculation (with MAPLE 8).
# Relative error of quantum clock
# i.e. with respect to one second:
delta := 10^(-18);
year := 31556926;
A_E := 4.543*10^9*year;
A_U := 13.7*10^9*year;
T := 2*A_U*A_E*delta/(A_U-A_E);
T := 0.4289777596
This means that two Quantum clocks must be running for about
half a second in order to observe the difference between an electron created at the Big Bang and an electron having the age of the earth.
Yes, such a huge difference in age can be quickly observed, in principle.
Our last calculation aims to establish the minimal difference in (orbital) time creation timestamps for electrons on Young Earth, as can in principle be observed with two contemporary quantum clocks, assuming that they keep running for one year starting here and now. $$ \delta \lt \frac{1}{2}\frac{T}{A^2} \Delta A \hieruit \Delta A \gt \frac{2A^2\delta}{T} $$ The result shall be expressed in years (giving a year squared in the denominator with the numerical calculation):
dA := 2*A_E^2*delta/year^2; # time in years
dA := 41.27769800
Ages of electrons that are created more than 42 years apart from each other on Young Earth can be distinguished in principle
with modern atomic clocks.