The Limited Validity
of Special Relativity
Let us repeat a "Gedanken - Experiment" by Albert Einstein; the purpose is to synchronize
two clocks. At that time, apparently, Einstein did not fully recognize the following fact:
"When reflected photons push back the reflecting object (recoil effect)
and change its velocity" (: Léon Brillouïn in Relativity
Reexamined, Academic Press 1970). Therefore, "The usual statement
of the relativity principle requires that frames of reference be extremely
heavy ... The old-fashioned principle of relativity is a dream;
it represents only a limiting case, but may not, for instance, be used without
much care when it comes to moving ... particles ... of very small masses
".
Instead of radar pulses which are essentially delta functions, as employed
by Einstein, we use more realistic pulses $\,\mbox{sinc}(2\pi t / \tau)$ , where
$\,\mbox{sinc}(x) = \sin(x) / x$ . These pulses are modulated with the signal
$\,\exp(i\omega t)\,$ of an atomic clock, while synchronizing the clocks of
laboratory O and laboratory O' :
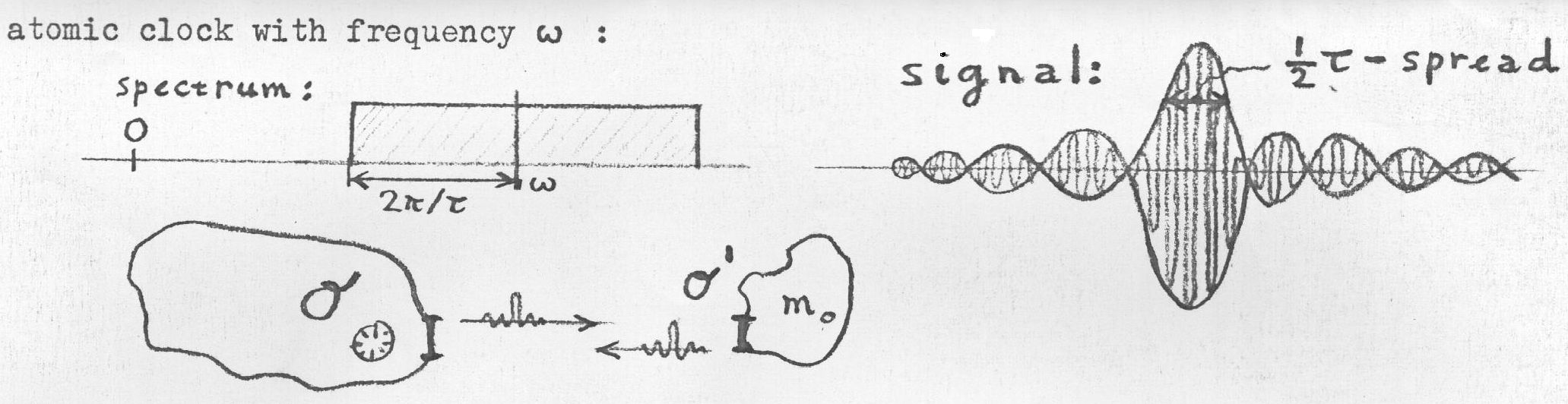
Where it is noticed that the Fourier spectrum of a $\mbox{sinc}(2\pi t / \tau)$
function is a Rectangular function, giving an (idealized) bandwidth $2\pi/\tau$ for the radar pulses.
After recoil, the wavelength of the carrier wave has become different
by Compton scattering,
because light waves interact with electrons - rest mass $m_0$ - in a reflector:
$$
\lambda' = 2\pi c/\omega + (\lambda' - \lambda) =
2\pi c/\omega + h / m_0 c (1-\cos \pi ) = 2\pi c/\omega + 2 h / m_0 c
$$
by Compton scattering .
But, in order for the pulse to be modulated, the following condition must be fulfilled:
$$
\omega' \gg 2\pi/\tau \quad \Longrightarrow \quad \tau/2 \gg \pi/\omega'
= \pi/(2\pi c/\lambda') = (\lambda'/c)/2 = \pi/\omega + h / m_0 c^2 > h/m_0 c^2
$$
Conclusion: the spread of the radar-pulses in time must be much greater
than the Compton time $= h / m_0 c^2$ , in order to
be able to synchronize clock O with clock O' of a reference frame with rest
mass $m_0$ . It is impossible to sychronize clocks within intervals
smaller than the Compton time.
In addition to the above, the following thought-experiment can be performed,
which affects the space-like part of the Lorentz transformations:

In somewhat more detail:
$$
\lambda' = \lambda + (\lambda' - \lambda) =
\lambda + h / m_0 c (1-\cos \pi/2 ) = \lambda + h / m_0 c
$$
Conclusion: the spread of the radar-pulses in space must be much greater
than the Compton (wave)length $= h / m_0 c$ , in order to be
able to compare lengths in O with those in O' of a reference frame with rest
mass $m_0$ . It is impossible to compare lengths within intervals
smaller than the Compton (wave)length.
Therefore, according to Wikipedia as well as according to the above,
the Compton wavelength expresses a fundamental limitation on measuring for
the position of a particle, taking into account quantum mechanics and special relativity.
Leaving aside the restrictions on relativistic time, we thus have:
-
(common length) - (relativistic length) ≫ (Compton wavelength of electron)
That's interesting, because it means that Special Relativity may be one of the very rare
theories in Physics that imposes a limit on its own validity. Let's do the mathematics:
$$
L - L\sqrt{1-\left(\frac{v}{c}\right)^2} \gg \lambda_C
\quad \mbox{where} \quad \lambda_C = \frac{h}{m_0 c}
$$
Step by step:
$$
1-\sqrt{1-\left(\frac{v}{c}\right)^2} \gg \frac{\lambda_C}{L} \\
\sqrt{1-\left(\frac{v}{c}\right)^2} \ll 1-\frac{\lambda_C}{L} \\
1-\left(\frac{v}{c}\right)^2 \ll \left(1-\frac{\lambda_C}{L}\right)^2 \\
\left(\frac{v}{c}\right)^2 \gg 1-\left(1-\frac{\lambda_C}{L}\right)^2 \\
\left|\frac{v}{c}\right| \gg \sqrt{2\frac{\lambda_C}{L}-\left(\frac{\lambda_C}{L}\right)^2} \\
\left|v \right| \gg c \; \sqrt{2\frac{\lambda_C}{L}-\left(\frac{\lambda_C}{L}\right)^2}
$$
Plug in some numbers:
$$
\lambda_C = 2.426 310 2389\times 10^{-12}\, m
\\ c = 299792458\,m/s \\ L = 1\, m
$$
Then the outcome is : ${\bf \left| v \right| \gg 660\, m/s}$ . With other words: when measuring
a rod of one metre, relativistic effects may come into play only for speeds (much) larger
than twice the speed of sound. As can be confirmed with a short program in (Delphi) Pascal:
program short;
const
c : double = 299792458;
L : double = 2.4263102389E-12;
begin
Writeln(c*sqrt(2*L/1-sqr(L/1)));
end.
Output:
6.60402739611352E+0002


