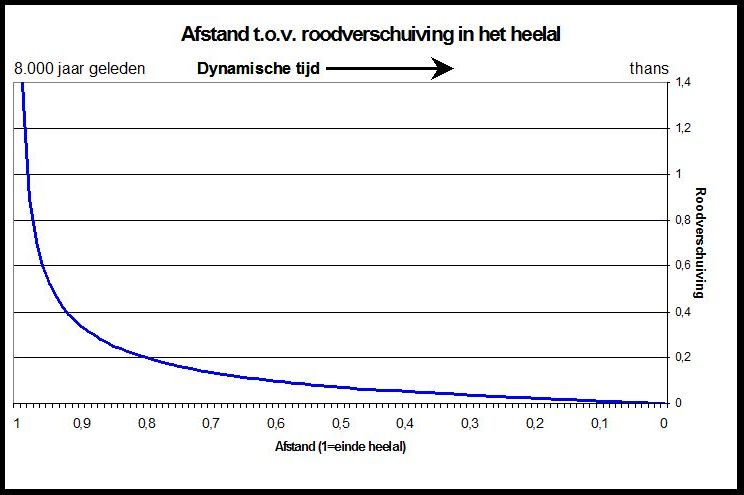
Barry Setterfield maakt in zijn theorie gebruik van twee klokken: een (dynamische) gravitatie-klok en een atoom-klok. Deze worden met elkaar in verband gebracht middels de enige formule in het artikel. Uitgaande van deze formule, andere elementen uit Setterfield's werk en wat hogere wiskunde kom ik tot een absurde bevinding: volgens de atoom-klok is Adam geschapen lang voordat de kosmos geschapen werd. Het heelal is in atoom-tijd namelijk niet 13,8 miljard jaar oud, zoals Barry Setterfield en Rinus Kiel beweren, foutief redenerend vanuit hun eigen theorie. Mijn berekening leert dat de schepping in atoom-tijd (Big Bang) plaats vond omstreeks 23 duizend jaar v.Chr, correct redenerend vanuit dezelfde theorie. Leeswaarschuwing: niet geschikt voor mensen zonder wiskundekennis.

De bij deze figuur bijbehorende formule is:
$$
z = \frac{1+(v/c)}{\sqrt{1-(v/c)^2}}-1
$$
De betekenis ervan wordt toegelicht in Setterfield's
The Speed of Light Curve ,
op de eigen website.
En wordt wiskundig "onderbouwd" in het document
THE REDSHIFT AND THE ZERO POINT ENERGY .
We hebben echter gezien dat Setterfield's wiskunde in dit laatste document van ondeugdelijke
kwaliteit is - onder andere helaas.
Er is in feite helemaal geen sprake van een wiskundige onderbouwing. Er is geen afleiding voor Setterfield's
roodverschuiving vergelijking, behalve dan dat deze gewoon een kopie is van de standaard relativistische formule
voor het Doppler effect. (Het is trouwens wel vreemd dat iemand die het niet eens is met de relativiteitstheorie
een relativistische formule kiest als $\color{blue}{\mbox{blauw}}$druk).
Maar laten we ons even beperken tot The Speed of Light Curve . Volgens dit document representeert de curve drie dingen, waarbij (1) de standaard relativistische formule voor het Doppler effect is. Niet toevallig in overeenstemming met de gangbare kosmologie, waarin het Doppler effect bovendien de verklaring is. Zoals gezegd, drie dingen:
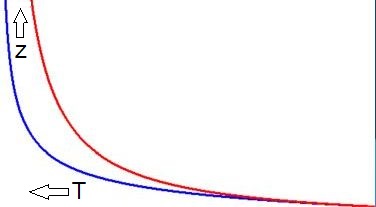
De bij deze figuur bijbehorende formules zijn (let op de kleuren):
$$
\color{blue}{z = \frac{1+T}{\sqrt{1-T^2}}-1} \quad ; \quad \color{red}{z = \frac{1}{1-T}-1}
$$
met $0 \le T \lt 1$ in omgekeerde richting (rechts naar links in plaats van links naar rechts).
Vooral in de buurt van het heden (rechts) lopen de verbanden weinig uiteen.
En dit zijn - in volgorde - de formules van de eigen theorie, betrokken op een referentie tijdstip $T_0$ en referentie waarden
$c_0,\lambda_0$ :
$$
\frac{\lambda}{\lambda_0} = \frac{A-T_0}{A-T} \qquad (1) \\
\frac{c_G}{c_0} = \frac{A-T_0}{A-T} \qquad (2) \\
\frac{dt}{dT} = \frac{A-T_0}{A-T} \qquad (3)
$$
Verklaring van de symbolen: $\lambda$ = golflengte van licht, $T$ = gravitatie tijd, $A$ = scheppingsmoment, $c$ = lichtsnelheid,
$G$ = met gravitatie klok gemeten, $t$ = atoom tijd.
De eerste formule hebben we nog niet eerder vermeld. Gemakkelijk is in te
zien dat : $\lambda/\lambda_0 = 1+z$ . Schalen en verplaatsen volgens $A=1$ en $T_0=0$ geeft dan de tweede vergelijking
$\color{red}{z=1/(1-T)-1}$ van daarboven terug.
De intuïtie van Setterfield is dus in zoverre mogelijk juist dat zowel
roodverschuiving, lichtsnelheid en atoomtijd aan dezelfde wet gehoorzamen: The truth of the matter is, these are all the same curve.
Andere ervaringen met zijn theorie in aanmerking genomen, is dit enigszins verbazingwekkend.
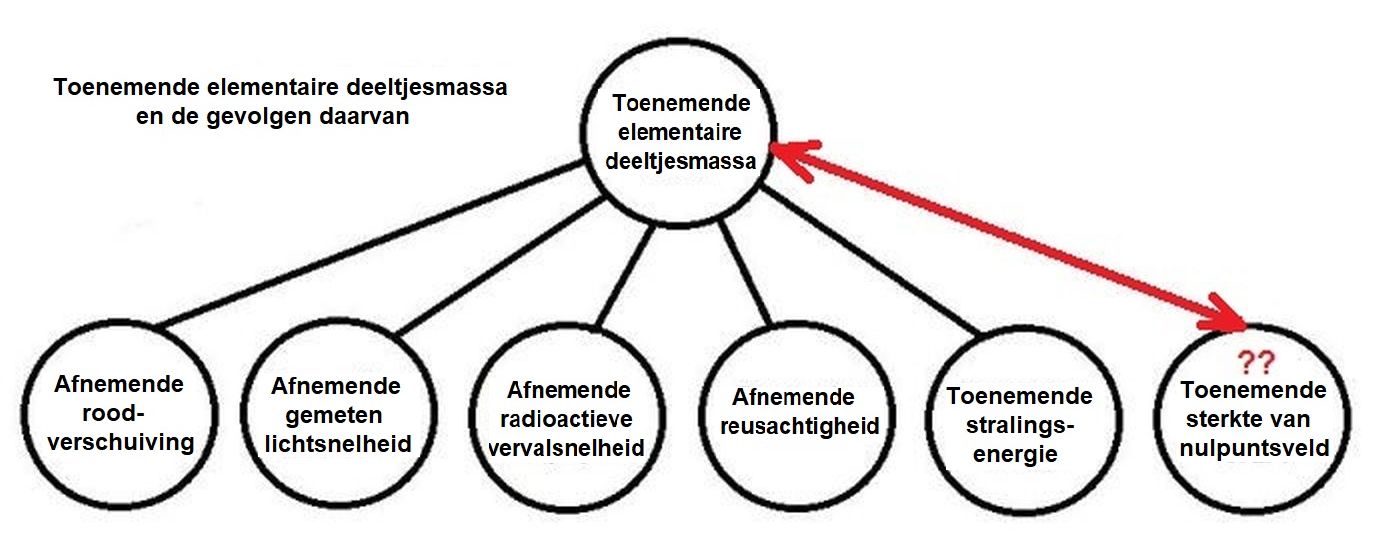
Maar we zijn er nog niet. In de ballonnetjes staan nog Afnemende
radioactieve vervalsnelheid en Afnemende reusachtigheid. Wiskundig uitgedrukt in de variabelen: $n$ = het aantal atoomkernen
per seconde wat vervalt, $L$ = grootte (van bijvoorbeeld een dinosaurus). Betrokken op referentie waarden $n_0,L_0$ krijgen we dan:
$$
\frac{n}{n_0} = \frac{A-T_0}{A-T} \qquad (4) \\
\frac{L}{L_0} = \frac{A-T_0}{A-T} \qquad (5)
$$
De Toenemende stralingsenergie en een eventueel Toenemende sterkte van het nulpuntsveld laten we even voor wat ze zijn.
Echter, wat zijn de gevolgen als we in plaats van de eigen opvatting die van Setterfield huldigen? Dan is met name:
$$
\frac{c_G}{c_0} = \frac{1+x}{\sqrt{1-x^2}} \quad \mbox{met} \quad x = T
$$
Met $c_G$ de lichtsnelheid gemeten met gravitatie-tijd en $c_0$ de lichtsnelheid gemeten met atoom-tijd; de laatste is een absolute constante.
Maar laten we de abscis $x$ zo aanpassen dat de coordinaat $T$ voortaan de echte gravitatie-tijd weergeeft en loopt van links naar rechts
in plaats van omgekeerd:
$$
\frac{c_G}{c_0} = \frac{1+x}{\sqrt{1-x^2}} \quad \mbox{met} \quad x = 1-\frac{T-A}{T_0-A}
$$
Dan is $x=1$ voor $T=A$ (: het scheppingsmoment) en $x=0$ voor $T=T_0$ (: het moment van heden). We wijken in niets af van Setterfield's theorie
door te stellen dat rate of ticking of the atomic clock against orbital time aan dezelfde wet voldoet. Dit volgt bovendien uit de
kettingregel voor het differentiëren in combinatie met de definitie van de lichtsnelheid als afgelegde weg $\,ds\,$ gedeeld door tijdstoename:
$$
\frac{c_G}{c_0} = \frac{ds}{dT}/c_0 = \frac{ds}{dt}\frac{dt}{dT}/c_0 = c_0/c_0 \frac{dt}{dT} \quad \Longrightarrow \\
\frac{dt}{dT} = \frac{1+x}{\sqrt{1-x^2}} \quad \mbox{met} \quad x = 1-\frac{T-A}{T_0-A}
$$
Merk op dat de gravitatie-klok gelijk loopt i.e. gelijk wordt gezet met de atoom-klok op het tijdstip heden $\,T=T_0=t=t_0$ :
$$
\left.\frac{dt}{dT}\right|_{x=0} = 1
$$
We gaan de vergelijking integreren, dat wil zeggen omzetten van infinitesimale tijdsintervallen naar echte tijd. Daartoe moeten we weten dat:
$$
dx = d\left(1-\frac{T-A}{T_0-A}\right) = -\frac{dT}{T_0-A} \quad \Longrightarrow \quad dT = -(T_0-A)dx
$$
Hiermee is:
$$
t-t_0 = \int dt = \int \frac{1+x}{\sqrt{1-x^2}}\,dT = -(T_0-A)\int \frac{1+x}{\sqrt{1-x^2}}\,dx
$$
Dit zadelt ons op met een paar elementaire integralen:
$$
\int \frac{1+x}{\sqrt{1-x^2}}\,dx = \int \frac{1}{\sqrt{1-x^2}}\,dx + \int \frac{x}{\sqrt{1-x^2}}\,dx =
\arcsin(x) - \frac{1}{2} \int \frac{d(1-x^2)}{\sqrt{1-x^2}}
$$
De laatste term is gelijk aan $\,-\sqrt{1-x^2}$ , zodat:
$$
t-t_0 = -(T_0-A)\left[\arcsin(x) - \sqrt{1-x^2} + C\right] \quad \mbox{met} \quad x = 1-\frac{T-A}{T_0-A}
$$
De integratie-constante $C$ moet zodanig worden aangepast dat de uitdrukking nul is voor $\,t=t_0$ :
$$
\arcsin(x) - \sqrt{1-x^2} + C = \arcsin(0) - \sqrt{1-0^2} + C = 0 \quad \Longrightarrow \quad C=1
$$
Dus uiteindelijk is dit het verband tussen atoom-tijd $\,t\,$ en gravitatie-tijd $\,T$ :
$$
t-t_0 = -(T_0-A)\left[\arcsin\left(1-\frac{T-A}{T_0-A}\right)-\sqrt{1-\left(1-\frac{T-A}{T_0-A}\right)^2}+1\right]
$$
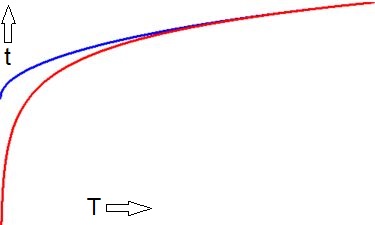
Volgt een grafische weergave van atoom-tijd als functie van gravitatie-tijd, volgens de Setterfield/Kiel theorie in
$\color{blue}{\mbox{blauw}}$ en volgens de Arp/deBruijn theorie in $\color{red}{\mbox{rood}}$. Dan zien we iets merkwaardigs:
in de $\color{blue}{\mbox{blauwe}}$ curve begint de atoomtijd $t$ op een eindige waarde, zij het met een scherpe knik
(afgeleide oneindig).
Laten we dus kijken naar de atoom-tijd $\,t=t_A\,$ op het moment van de schepping in gravitatie tijd $\,T=A$ . Dan is $x=1$ of:
$$
1-\frac{T-A}{T_0-A} = 1 \quad \Longrightarrow \quad t_A-t_0 = -(T_0-A)\left[\arcsin(1)-\sqrt{1-1^2}+1\right] \quad \Longrightarrow \\
t_A = T_0 - (T_0-A)\left[\frac{\pi}{2}+1\right] \quad \Longrightarrow \quad t_A = A - \frac{\pi}{2}(T_0-A)
$$
Om de gedachten te bepalen, als het scheppingstijdstip is $A = -8000$ en het heden $T_0 = 2018$ , dan is:
$$
t_A \approx -8000 - \pi/2 \times (2018+8000) \approx 23,736 \; \mbox{Jaar v.Chr.}
$$
Dus de schepping in atoomtijd vond plaats omstreeks 23 duizend jaar voor Christus. Moet dit dan geïnterpreteerd worden als
het (atoom)jaar van de Big Bang? Ik denk niet dat de seculiere wetenschap blij zal zijn met deze uitkomst. Maar de creationistische
wetenschapsopvatting van Setterfield is hier evenmin mee in overeenstemming, getuige de volgende grafiek, die afkomstig is uit het
dosument ANCIENT CHRONOLOGY IN SCRIPTURE © Barry Setterfield, September 1999:
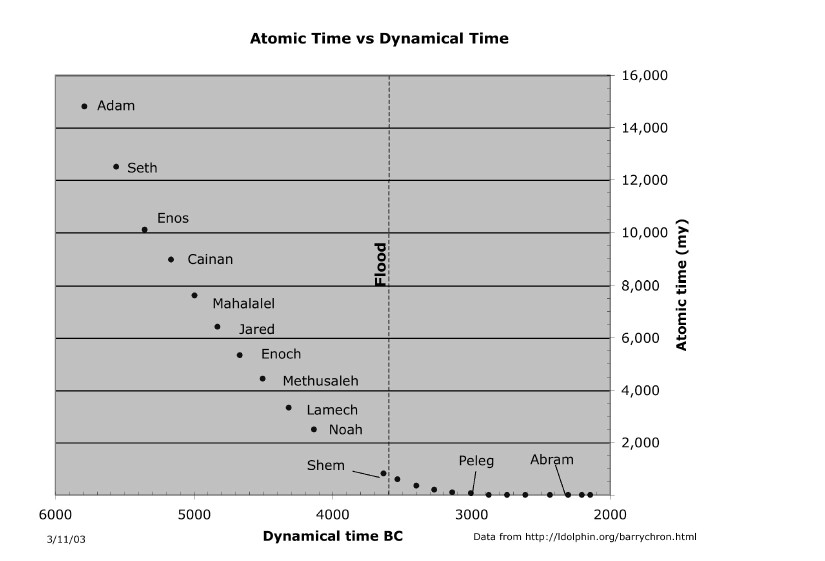
Volgens deze figuur zou de schepping van Adam in atoomtijd miljoenen jaren eerder zijn geschied dan het heelal in atoomtijd oud is.
Dit is uiteraard absurd. Hieruit blijkt eens te meer dat Setterfield de consequenties van zijn eigen theorie niet kan overzien. Het
is - niet alleen voor hem maar ook voor anderen - een onbeheersbaar geheel, zoals ik al eerder heb betoogd.