
index $ \def \hieruit {\quad \Longrightarrow \quad} \def \slechts {\quad \Longleftrightarrow \quad} \def \SP {\quad ; \quad} \def \MET {\quad \mbox{with} \quad} \def \EN {\quad \mbox{and} \quad} \def \half {\frac{1}{2}} $
Gravitational deflection of light is the second classical test on General Relativity. Quote mining is from Newtonian gravitational deflection of light revisited as well: $$ \delta \phi_{E} = \frac{4GM_S}{c^2R_S} \SP \delta \phi_{N} = \frac{2GM_S}{c^2R_S} $$ Here $\,\delta \phi$ are the deflection angles, according to Einstein and Newton respectively. $G$ is the Gravitational constant, $M_S$ is the mass of our sun, $R_S$ is the radius of our sun $= 696,340\;km\,$, $c$ is the speed of light $= 299,792,458\;m/s\,$. The outcome with General Relativity is commonly thought to be twice the outcome with Newton Gravity. However, I have found some "Accurate Solution to the Gravitational Bending of Starlight by a Massive Object", showing that $\delta_{NG}$ would be exactly the same as $\delta_{GR}$ ! One reason for the twist seems to be that the kinetic energy of a photon, according to Special Relativity, is $\,mc^2\,$ instead of $\,\half mc^2\,$ as assumed in Newtonian mechanics. If the document holds water, then General Relativity is doomed to become redundant, at least insofar Light Bending is concerned. I find this difficult to believe, though. Let us divide potential energy by kinetic energy in both cases, then the Einstein solution comes out the wrong way: $$ \delta \phi_{E} = \frac{GM_Sm/R_S}{mc^2} = \frac{GM_S}{c^2R_S} \SP \delta \phi_{N} = \frac{GM_Sm/R_S}{\half mc^2} = \frac{2GM_S}{c^2R_S} $$ I have decided to recapitulate the Newtonian version of the bending, in order to be completely certain. Let's start with some mathematics: Equations of Hyperbolas.
 \begin{align*}
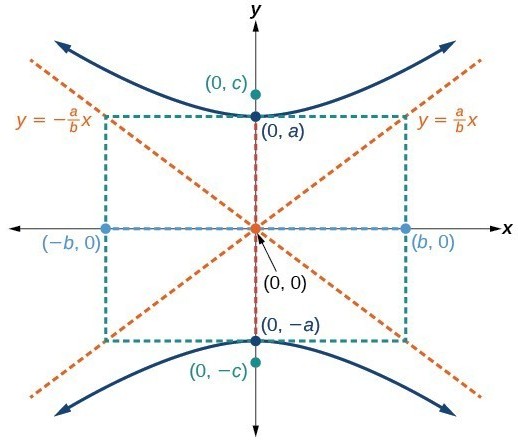
\mbox{Hyperbola equation:} \qquad & \frac{y^2}{a^2}-\frac{x^2}{b^2}=1 \hieruit y=-a\sqrt{1+\frac{x^2}{b^2}} \\
\mbox{Asymptotic lines:} \qquad & y = \pm \frac{a}{b}x \\
\mbox{Focus coordinates:} \qquad & (x,y) = (0,-c) \quad \mbox{with} \quad c = \sqrt{a^2+b^2} \\
\mbox{Radius of the sun:} \qquad & R_S = c-a \\
\mbox{Excentricity:} \qquad & e = \sqrt{1+\left(\frac{b}{a}\right)^2}
\end{align*}
From a physics perspective, we have the Orbital eccentricity:
$$
e = \sqrt{1+\frac{2\epsilon h^2}{\mu^2}}
$$
With $\,\epsilon\,$ as the Specific orbital energy or
vis-viva energy. The Vis-viva equation is, in our case
$$
v^2(r) = V^2 + 2GM\left(\frac{1}{r}-\frac{1}{r_0}\right) \MET r_0=\infty \EN V = v_\infty
$$
The vis-viva energy for a hyperbola is related to the the orbital velocity at infinity $\,v_\infty\,$.
The other two quanties are the Standard
gravitational parameter $\,\mu\,$ and the Specific
angular momentum $\,h\,$. Let $\,v_S\,$ the velocity of the test body near the sun. The angular momentum is conserved.
This means that $\,h\,$ has to be evaluated for a simple special case only, which is spotted to be closest to the sun:
$\,\vec{r} \times \vec{v} = R_S v_S\,$. Because our satellites are photons, $\,v_\infty\,$ is at lightspeed $\,c\,$.
Summarizing:
$$
2\,\epsilon = v_\infty^2 \SP \mu = GM_S \SP h = R_S v_S \quad \mbox{where} \quad v_\infty = c
$$
The Vis-viva equation for the hyperbola combined with Wikipedia's
Deflection of light by the Sun shows that the velocity $\,v_S\,$ cannot be distinguished from lightspeed as well.
$$
v_S^2 = \frac{2GM}{R_S} + v_\infty^2 \hieruit v_S = c\,\sqrt{1+\frac{2GM}{c^2R_S}} =
c\,\sqrt{1+\frac{1.75/2}{360\times 60\times 60}} \hieruit v_S \approx c
$$
Now the physical eccentricity is equal to the mathematical eccentricity:
$$
e = \sqrt{1+\frac{v_\infty^2 (R_Sv_S)^2}{(GM_S)^2}} = \sqrt{1+\left(\frac{c^2R_S}{GM_S}\right)^2} = \sqrt{1+\left(\frac{b}{a}\right)^2}
\hieruit \frac{a}{b} = \frac{GM_S}{c^2R_S}
$$
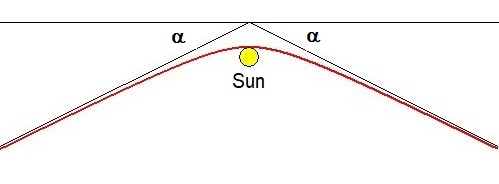
We are almost there. The slopes of the asymptotes of the hyperbola are given by $\,\tan(\alpha) = \pm a/b\,$. Where $\alpha$
is a very small angle, meaning that $\,\tan(\alpha) \approx \alpha\,$. From the pictures it is clear that we must take
twice that angle in order to obtain the final deflection:
$$
\delta \phi_{N} = 2\alpha = \frac{2GM_S}{c^2R_S}
$$
This is perhaps the most concise derivation of Gravitational Light Bending you have ever seen. Apart from that, we must
conclude that the common view upon Gravitational Light Bending is alright: Newtonian mechanics explains only half of it.
\begin{align*}
\mbox{Hyperbola equation:} \qquad & \frac{y^2}{a^2}-\frac{x^2}{b^2}=1 \hieruit y=-a\sqrt{1+\frac{x^2}{b^2}} \\
\mbox{Asymptotic lines:} \qquad & y = \pm \frac{a}{b}x \\
\mbox{Focus coordinates:} \qquad & (x,y) = (0,-c) \quad \mbox{with} \quad c = \sqrt{a^2+b^2} \\
\mbox{Radius of the sun:} \qquad & R_S = c-a \\
\mbox{Excentricity:} \qquad & e = \sqrt{1+\left(\frac{b}{a}\right)^2}
\end{align*}
From a physics perspective, we have the Orbital eccentricity:
$$
e = \sqrt{1+\frac{2\epsilon h^2}{\mu^2}}
$$
With $\,\epsilon\,$ as the Specific orbital energy or
vis-viva energy. The Vis-viva equation is, in our case
$$
v^2(r) = V^2 + 2GM\left(\frac{1}{r}-\frac{1}{r_0}\right) \MET r_0=\infty \EN V = v_\infty
$$
The vis-viva energy for a hyperbola is related to the the orbital velocity at infinity $\,v_\infty\,$.
The other two quanties are the Standard
gravitational parameter $\,\mu\,$ and the Specific
angular momentum $\,h\,$. Let $\,v_S\,$ the velocity of the test body near the sun. The angular momentum is conserved.
This means that $\,h\,$ has to be evaluated for a simple special case only, which is spotted to be closest to the sun:
$\,\vec{r} \times \vec{v} = R_S v_S\,$. Because our satellites are photons, $\,v_\infty\,$ is at lightspeed $\,c\,$.
Summarizing:
$$
2\,\epsilon = v_\infty^2 \SP \mu = GM_S \SP h = R_S v_S \quad \mbox{where} \quad v_\infty = c
$$
The Vis-viva equation for the hyperbola combined with Wikipedia's
Deflection of light by the Sun shows that the velocity $\,v_S\,$ cannot be distinguished from lightspeed as well.
$$
v_S^2 = \frac{2GM}{R_S} + v_\infty^2 \hieruit v_S = c\,\sqrt{1+\frac{2GM}{c^2R_S}} =
c\,\sqrt{1+\frac{1.75/2}{360\times 60\times 60}} \hieruit v_S \approx c
$$
Now the physical eccentricity is equal to the mathematical eccentricity:
$$
e = \sqrt{1+\frac{v_\infty^2 (R_Sv_S)^2}{(GM_S)^2}} = \sqrt{1+\left(\frac{c^2R_S}{GM_S}\right)^2} = \sqrt{1+\left(\frac{b}{a}\right)^2}
\hieruit \frac{a}{b} = \frac{GM_S}{c^2R_S}
$$
We are almost there. The slopes of the asymptotes of the hyperbola are given by $\,\tan(\alpha) = \pm a/b\,$. Where $\alpha$
is a very small angle, meaning that $\,\tan(\alpha) \approx \alpha\,$. From the pictures it is clear that we must take
twice that angle in order to obtain the final deflection:
$$
\delta \phi_{N} = 2\alpha = \frac{2GM_S}{c^2R_S}
$$
This is perhaps the most concise derivation of Gravitational Light Bending you have ever seen. Apart from that, we must
conclude that the common view upon Gravitational Light Bending is alright: Newtonian mechanics explains only half of it.
If such is the case, then perhaps there is another way out. The cogravitation constant times the mass of the sun is:
$$
\gamma.M_S = \frac{4\pi GM_S}{c^2}
$$
And it has the dimension of length.
When considering the dimensionless deflection $\,\delta \phi\,$ of light around the sun we need another length
to divide with. That other length cannot be anything else than the radius of the sun, or some length derived from it
- the perimeter of the sun's Great circle would be great $= \,2\pi R_S\,$.
This might give an additional deflection with the same magnitude as the Newtonian one. Possibly resulting in the correct
outcome after all:
$$
\delta \phi_{E} = \delta \phi_{N} + \frac{4\pi GM_S}{c^2\,2\pi R_S} = \frac{2GM_S}{c^2R_S} + \frac{2GM_S}{c^2R_S} = \frac{4GM_S}{c^2R_S}
$$
However, there might be a much simpler approach.
The definition of the Specific orbital energy is resumed first:
$$
\varepsilon = \varepsilon_k + \varepsilon_p = \frac{v^2}{2}-\frac{\mu}{r} % \SP \delta \phi_{N} = \frac{2GM_S}{c^2R_S}
% = - \left.\frac{\varepsilon_p}{\varepsilon_k}\right|_S
$$
Here we see that $\varepsilon _{k}$ corresponds with kinetic energy, which according to Newtonian mechanics is $\half mv^2$.
However, this is wrong for photons, where according to Special Relativity the kinetic energy is equal to $mc^2$ instead of $\half mc^2$.
It's the same error as in The Theory of Heat Radiation
at page 58, where it is argued by Max Planck that
Newton's radiation pressure is twice as large as Maxwell's for the same energy radiation. But if $\half mc^2$ in his
formula (68) is replaced by the correct $mc^2$ then the two approaches - waves versus particles / Maxwell versus Newton - lead to
exactly the same results in the book by Max Planck.
So let's put $\epsilon = v_\infty^2 = c^2$ instead of $2\,\epsilon = v_\infty^2 = c^2$ and look what happens.
$$
e = \sqrt{1+\frac{2v_\infty^2 (R_Sv_S)^2}{(GM_S)^2}} = \sqrt{1+\left(\frac{\sqrt{2}\,c^2R_S}{GM_S}\right)^2}
= \sqrt{1+\left(\frac{b}{a}\right)^2} \hieruit \frac{a}{b} = \frac{GM_S}{\sqrt{2}\,c^2R_S}
$$
The deflection becomes smaller instead of larger; it's the wrong way around :-(
From Relativity Reexamined at page 98 we quote:
For instance, Einstein predicts the deflection of a light ray passing near the surface of the sun,
but we obtain a similar result if we consider a light ray as a beam of photons $\,h\nu\,$ with masses $\,h\nu/c^2\,$.
Only the numerical coefficient is different, and Einstein's prediction is twice as large as that in the computation with photons.
Here the experimental results are actually very poor, with errors of 100% magnitude; a detailed discussion of older results may
be found in Ghazy's book (1930), and more recent experiments were no better; looking candidly at these observations, one feels
that very large sources of error are obviously playing a substantial role, and our present knowledge of the turbulent flow in the solar
atmosphere yields the most probable explanation. The Shapiro (1968) experiment is certainly safer than the deflection of light
rays. Let us emphasize the importance of the solar wind that corresponds to ten million tons of matter annihilated per second and
radiated away!
Another approach to the problem is presented in the section Dicke's proposal (1957) of the Wikipedia page about a
Variable speed of_light.
Robert Dicke, in 1957, developed a VSL theory of
gravity, a theory in which (unlike general relativity) the speed of light measured locally by a free-falling observer could vary.
Dicke assumed that both frequencies and wavelengths could vary, which [ .. ] resulted in a relative change of $\,c_0\,$.
Dicke assumed a refractive index [ .. ] and proved it to be consistent with the observed value for light
deflection:
$$
n = 1 + \frac{2GM}{r\,c_0^2}
$$
Upon further investigation it is discovered that Robert Dicke is not the first one who proposed a Variable Speed of Light, with
the gravity field as a refractive medium. It's already in Einstein's 1911 Paper, translated in English as:
On the Influence of Gravitation on the Propagation of Light. On page 903 we find formula (3), where $c$ is the VSL
according to A. Einstein at that time.
$$
c = c_0 \left(1 + \frac{\Phi}{c_0^2}\right) \MET \Phi = \frac{GM}{r} \slechts n = 1 + \frac{GM}{r\,c_0^2}
$$
Exactly half of the value by Dicke, which is understandable, because the latter is after the advent of General Relativity. We quote from
6.3 Bending Light: The idea of bending light was revived in
Einstein's 1911 paper "On the Influence of Gravitation on the Propagation of Light". Oddly enough, the quantitative prediction given in
this paper for the amount of deflection of light passing near a large mass was identical to the old Newtonian prediction. Details
are explained in Doubling the Deflection.