Tegen de stroom in

De opvatting dat numerieke oplossingen een min of meer gebrekkige benadering zijn van "exakte" oplossingen, die de klassieke analyse ons zou leveren, is om verschillende redenen onjuist.

Om te beginnen levert de klassieke analyse ons deze oplossingen meestal niet. Ho, wacht eens even, de oplossing "bestaat" theoretisch wel, want dat kunnen we "bewijzen". We kunnen haar alleen niet uitrekenen! De naakte existentie van oplossingen, volgens de niet-konstruktieve wiskunde van de Formalistische school, weten we het nog? Als Toegepast Wiskundige heeft men weinig of geen houvast aan zulke niet-konstruktieve opvattingen.

Daarom is het ook niet zinvol te verlangen dat de numerieke oplossing naar de analytische oplossing konvergeert. Wél korrekt daarentegen is de opvatting dat analytische oplossing en numerieke oplossing, indien beide bestaan, naar dezelfde waarden moeten konvergeren.

Het is bovendien niet redelijk te veronderstellen dat numerieke oplossingen gemakkelijker de fout in gaan dan analytische. Ook in de afleiding van een ingewikkelde analytische oplossing kunnen "bugs" zitten.

Teneinde de gangbare opvatting versus die van ons te illustreren, volgt hier een fragment uit [Ames]. (Partiële) Differentiaalquotiënten kunnen op velerlei manieren worden benaderd door eindige differenties. Door al dit soort van benaderingen worden fouten geïntroduceerd, afbreekfouten genaamd. De aanwezigheid ervan zal worden aangeduid door middel van de asymptotische $O$ notatie. Ames behandelt vervolgens een aantal schema's in twee dimensies. Het is alleszins voldoende ons te beperken tot de één dimensionale weergave van dit betoog. Beschouw een uniform raster in 1-D.

De afstand tussen twee naburige punten in het rekenraster bedraagt $h$. Laat een willekeurige funktie $f$ gediskretiseerd worden als waarden $f_i$ op de punten van het raster. Ontwikkel $f$ in een Taylor-reeks: $$ f(x+h) \approx f(x) + h.f'(x) + \frac{h^2}{2!} f''(x) + \frac{h^3}{3!}f'''(x) $$ Hieruit volgt: $$ f'(x) \approx \frac{ f(x+h) - f(x) }{ h } - \frac{f''(x)}{2}\, h $$ Specificeer $x$ voor de rasterpunten: $$ f'_i \approx \frac{1}{h} [ f_{i+1} - f_{i} ] + O(h) $$ De grootheid $O(h)$ vertegenwoordigt de asymptotische notatie voor de "afbreekfout" van de benadering. Blijkbaar is de fout hier "van de eerste orde". Beschouw naast de reeksontwikkeling van hierboven ook de volgende: $$ f(x-h) \approx f(x) - h.f'(x) + \frac{h^2}{2!} f''(x) - \frac{h^3}{3!}f'''(x) $$ En trek de twee van elkaar af. Dan komt er: $$ f(x+h) - f(x-h) \approx 2.h.f'(x) + 2 \frac{h^3}{3!} f'''(x) $$ Hieruit volgt: $$ f'_i \approx \frac{1}{2h} [ f_{i+1} - f_{i-1} ] + O(h^2) $$ In tegenstelling tot de eerste benadering is deze "van de tweede orde". Men is in mathematische kring geneigd aan te nemen dat zo'n tweede orde differentie schema de voorkeur verdient boven een dat "slechts van de eerste orde" is.

We zullen nu laten zien tot welk een absurd resultaat deze opvatting aanleiding geeft. Beschouw de volgende uiterst eenvoudige differentiaalvergelijking: $$ \frac{dT}{dx} = 0 \qquad \mbox{met randvoorwaarde:} \quad T(0)=1 $$ Diskretiseer met behulp van het "tweede orde nauwkeurige" schema: $$ T_1 = 1 \; ; \; (T_3 - T_1)/2h = 0 \; ; \; (T_4 - T_2)/2h = 0 \; ; \; (T_5 - T_3)/2h = 0 \; ; \; ... $$ Hieruit volgt: $$ ... \; = T_5 = T_3 = T_1 = 1 \; ; \; ... \; = T_6 = T_4 = T_2 = \mbox{volkomen willekeurig} $$ Een korrekte oplossing wordt alleen gevonden voor de oneven rasterpunten. Door het "tweede orde" schema worden de waarden op de even en de oneven punten namelijk volledig van elkaar ontkoppeld. Wie nu mocht denken dat professionals in het vakgebied zulke voor de hand liggende fouten niet zullen begaan, moet ik bij deze teleurstellen. Bij het diskretiseren van de stromingsvergelijkingen (Navier Stokes) met behulp van de methode van Galerkin is men destijds gestuit op het verschijnsel van de "schaakbord druk" (chequerboard pressure). Een (tamelijk eenvoudige) analyse brengt aan het licht dat het hier gaat om in wezen hetzelfde fenomeen als hierboven: twee geheel ontkoppelde om-en-om "oplossingen". Men werd (en wordt?) van een beter begrip van het verschijnsel weerhouden door de ogenschijnlijk veel grotere ingewikkeldheid van het Navier-Stokes probleem.

We hebben het inmiddels over vergelijkingen voor konvektieve stromingen. Een voorbeeld wat iedereen kent is het transport door stromend water van warmte in een centrale verwarming. Keren we even terug naar onze zeer eenvoudige gewone differentiaalvergelijking $ dT/dx = 0 $ of wat uitgebreider: $ u.dT/dx = 0 $ met $ u>0 $. Dit is niets anders dan de dan de allersimpelste analytische beschrijving die men kan bedenken voor het probleem van konvektie in het ééndimensionale geval.

Eigenlijk heeft alleen de eindige Differentie methode qua numerieke traditie de middelen in huis om konvektieve verschijnselen afdoende te behandelen. De diskretisatie schema's die met konvektie samenhangen worden "tegenstroom" (engels: "upwind") schema's genoemd. Het volgende is een vrije vertaling uit Patankar [SV]. De kontrole volumes [ eigen aan de eindige "volumen" methode ] kunnen worden opgevat als roerbakken die achter elkaar zijn geschakeld door middel van korte buizen. De stroming door deze buizen geeft de konvektie weer. [ ... ] Omdat de bakken worden geroerd, bevat iedere bak vloeistof met een gelijkmatige temperatuur. Dan is het toepasselijk te veronderstellen dat de vloeistof in elke verbindingsbuis de temperatuur heeft die heerst in de bak welke stroomopwaarts gelegen is. Normaal gesproken kan de vloeistof in de buis niets weten over de bak waar hij naar toe stroomt, maar neemt wel alles met zich mee van de bak waar hij vandaan komt. Dit is de essentie van het tegenstroom schema. Einde Patankar's betoog. Zelf heb ik dit roerbakken model ooit opnieuw uitgevonden, en gebruikt bij het berekenen van asymmetrische temperaturen in het bovengedeelte van een natriumpomp (Neratoom). Verder blijkt het idee mathematisch overeen te komen met het differentie-schema dat we hierboven het eerst van al hebben afgeleid, dat is het schema van de eerste orde: $$ f'_i \approx \frac{1}{h} [ f_{i+1} - f_{i} ] + O(h) $$ Resulterend in: $$ T_1 = 1 \; ; \; (T_2 - T_1)/h = 0 \; ; \; (T_3 - T_2)/h = 0 \; ; \; (T_4 - T_3)/h = 0 \; ; \; ... $$ Hieruit volgt: $$ ... \; = T_5 = T_4 = T_3 = T_2 = T_1 = 1 $$ En dit is exakt de korrekte oplossing, op alle even en oneven punten. Het schema van de eerste orde is dus, zeker voor dit specifieke geval, oneindig veel beter dan het, volgens menig wiskundige nauwkeuriger, schema van de tweede orde.

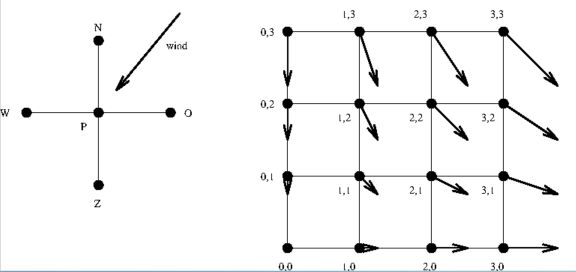
Kern van de eindige Differentie methode voor konvektie is het "upwind" schema, het nemen van differenties tegen de wind in. Om dit beter te begrijpen, bekijken we een stuk van een 2-D homogeen (rechthoekig, equidistant) eindige differentie raster. De mogelijke windrichtingen Noord, Zuid, Oost en West zijn dienovereenkomstig aangeduid. Dit is geen grap: de professionele aanpak van het probleem gaat op dezelfde manier. A propos, de Professionele waarnemer in ons verhaal wordt geacht plaats te nemen ter plekke $P$. Stel nu dat we te maken hebben met noordoosten wind, ofwel konvektie in het kwadrant $PON$. Men gaat ervan uit dat zo'n windrichting altijd kan worden ontbonden: in een oostelijke komponent $U$ en een noordelijke komponent $V$. Stel dat in het oosten een temperatuur $T_O$ en in het noorden een temperatuur $T_N$ heerst. Bepalend voor de temperatuur $T_P$ ter plaatse $P$ van de waarnemer zijn dan, behalve de temperatuur $T_P$ ter plaatse, uitsluitend de omgevingstemperaturen $T_O$ en $T_N$. Natuurlijk doen alleen eindige differenties tegen-de-wind-in ter zake: $(T_O-T_P)$ en $(T_N-T_P)$. Warme wind uit bijvoorbeeld het Zuiden komt in ons geval niet aangewaaid, en dus kan een invloed van de bijbehorende temperatuur niet worden gevoeld. Enkel de koude luchtmassa's uit Noord en Oost komen samen ter plekke $P$, en oefenen hun invloed uit, volgens de eenvoudige natuurwet van het verschijnsel dat we mengen noemen: $$ U.(T_O-T_P) + V.(T_N-T_P) = 0 $$ Hierin is: $U=$ horizontale component van het debiet, $V=$ vertikale component van het debiet (: vergelijk "Vierkante bellen"). Dit is het klassieke tweedimensionale tegenwind eindige differentie schema voor zuivere konvektie. Men kan uit de litteratuur opmaken dat het aanvankelijk ook een behoorlijk "tegendraads" schema was. Tot op de dag van vandaag zijn er heel wat mensen die er niet aan willen geloven.

Het tegenwind schema is slechts "van de orde $O(h)$", en zou bijvoorbeeld niet nauwkeurig genoeg zijn. Laten we deze veronderstelling maar meteen pareren met een tegenvoorbeeld. Beschouw zuivere konvektie van warmte in een vlakke ideale stroming die de binnenkant van een rechte hoek neemt. De snelheidsverdeling in deze stroming is bekend op grond van een analytische oplossing. Wanneer men het stromingsveld voorziet van een uniform 4 bij 4 raster met een index $i$ voor de $x$-richting en een index $j$ voor de $y$-richting, dan worden de snelheden $(u,v)$ op een konstante na gegeven door: $$ u = i \qquad ; \qquad v = - j $$ Bijbehorende debieten zijn positief: $U=u$ en $V=-v$. Uitwerking van het tegenstroom schema voor de temperaturen resulteert nu in: $$ (i+j).T_{i,j} = i.T_{i-1,j} + j.T_{i,j+1} $$ Neem op de instroomrand, die bovenaan zit, een lineair temperatuurprofiel aan, voor het gemak met de waarden $0,1,2,3$. Omdat de wand een stroomlijn is, zijn daar alle temperaturen gelijk aan de waarde $0$. Nu kunnen de temperaturen in de rest van het veld handmatig worden berekend, om te beginnen voor $(1,2)$: $$ (1+2).T_{1,2} = 1.0 + 2.1 = 2 \quad \Longrightarrow \quad T(1,2) = 2/3 $$ Na afloop van 6 van deze eenvoudige berekeningen ziet het temperatuurveld er als volgt uit:

        0     1     2     3
        0    2/3   4/3    2
        0    1/3   2/3    1
        0     0     0     0

Kort en goed, het moet nu maar eens uit zijn met dat ge-$O(h)$ over de "eerste orde nauwkeurigheid" van upwind schema's.

Laten we de partiële differentiaalvergelijking vermelden waar het 2-D upwind schema de materialisatie van is. Of laten we vermelden welke differentiaalvergelijking van het tegenstroom schema de idealisatie is. Beide beweringen zijn elkaars complement. We hadden ook kunnen zeggen: laat ons zien wat de analytische benadering van het tegenstroom schema is. We willen hiermee af van het Idee dat de analytische benadering de werkelijkheid per definitie beter zou beschrijven dan het numerieke schema. Waarbij moet worden aangetekend dat het numerieke schema dan wel enigzins abstrakt moet worden opgevat: zo moet onder andere worden afgezien van de konkrete verdeling van rasterpunten in het vlak. De bedoelde abstraktie moet worden mogelijk gemaakt door een uniforme numerieke wiskunde [FTP]. Maar er is geen enkele reden om gelaten op de toekomst te gaan zitten wachten. Men kan namelijk nu reeds met zekerheid stellen dat alle schema's, willen ze serieus in aanmerking komen als kandidaat voor een praktische numerieke beschrijving van de konvektieve termen, op een of andere manier een "upwind" karakter moeten hebben. En het is nu reeds ondenkbaar dat in een veralgemeniseerde numerieke beschrijving deze eigenschap niet onverkort gehandhaafd zal blijven.

Het is bekend dat het tegenstroom schema convergeert naar de overeenkomstige partiële differentiaalvergelijking. Over de mate waarin dat gebeurt lopen de meningen uiteen. Maar wanneer we uitgaan van een maaswijdte in de orde van de gemiddelde vrije weglengte tussen twee moleculen, dan zal de tegenstroom "benadering" fysisch niet te onderscheiden zijn van "exakt". Het omgekeerde is echter beslist niet waar. Wanneer we in plaats van het analytische model het tegenstroom schema opvatten als de echte natuurwet, dan is de partiële differentiaalvergelijking toch altijd iets verschillend van het overeenkomstige numerieke schema. Was in de numerieke benadering namelijk de richting van de stroming te herkennen - logisch, want dat is precies wat met "upwind" wordt beoogd - in de analytische benadering is deze richtingsgevoeligheid plotseling en spoorloos verdwenen. Wij hebben nochthans de tegenstroom voorwaarde op grond van deugdelijke argumenten, mathematisch en fysisch, naar voren gebracht. De gevolgtrekking ligt voor de hand dat in de analytische formulering dan op de een of andere manier wezenlijke informatie wordt verdonkeremaand.

Het numerieke tegenstroom schema bevat richtingsinformatie welke voor konvektie essentieel is. Na idealisatie tot een partiële differentiaalvergelijking is deze informatie echter spoorloos verdwenen.

Men zou de konklusie kunnen trekken dat de analytische benadering op het punt van de richtingsgevoeligheid zelfs inferieur is aan de numerieke benadering. Jazeker, daar mag men aan denken.

Wij naderen de climax van dit hoofdstuk. Beschouw namelijk de volgende variant op de natuurwet voor konvektie: $$ \frac{\partial T}{\partial t} + u . \frac{\partial T}{\partial x} = 0 $$ Er is geen enkele reden om deze differentiaalvergelijking, waar nu de tijd in voorkomt, op een andere manier te diskretiseren dan de konvektie vergelijking voor het platte vlak. Het ligt bovendien voor de hand om, precies zoals dat het geval is in de relativiteitstheorie, ruimte en tijd te behandelen op voet van gelijkheid. In de meest succesvolle variant van de eindige Differentie methode volgens [SV] is dit trouwens ook de praktijk. In het geval van een uniform raster, en een positieve snelheid $u$, wordt het volgende tegenstroom schema afgeleid: $$ \frac{1}{\Delta t} (T_P - T_Z) + \frac{u}{\Delta x} (T_P - T_W) = 0 $$ En nu komt het: het is ogenblikkelijk in te zien dat dit schema, behalve voor de omkering van de snelheid, ook niet invariant is voor omkering van de tijd! Aangenomen dat Tegenstroom Differenties echte natuurwetten representeren, moet worden vastgesteld dat met name ook de richting waarin tijd "stroomt" niet zomaar kan worden omgekeerd. Met grote overtuiging durven wij zelfs stellen:

TIJD is ONOMKEERBAAR. De omkeerbaarheid van de tijd is een illusie die louter en alleen te danken is aan verlies aan informatie over de richting, binnen de klassieke analytische formulering van de natuurwetten.

In het numerieke werk is de ervaring dat iedere poging de tijdrichting om te keren onmiddelijk wordt bestraft door het optreden van instabiliteiten.

Maar ook in toepassingen van de klassieke analyse blijkt dat deze verloren informatie vaak weer als een extra gegeven, achteraf, moet worden aangebracht. Ik kan mij uit een college ElektroTechniek bijvoorbeeld een "causaliteitsprincipe" herinneren van deze strekking. En wat denkt men van zaken als het zomaar weglaten van oplossingen van de golfvergelijking die naar de verstoring toelopen, in plaats van ervandaan? Alleen maar omdat zoiets fysisch toch echt onbestaanbaar is! Het geheim ligt in de onttroning van de klassieke analyse als enig mogelijk kader. Door te erkennen dat numerieke (tegenstroom) schema's, met even veel recht als analytische benaderingen, aanspraak kunnen maken op het voeren van de titel "natuurwet", kan men het probleem van de onomkeerbaarheid van de tijd oplossen. Werd het niet de hoogste tijd?